kmp算法python实现

kmp算法python实现

kmp算法

kmp算法用于字符串的模式匹配，也就是找到模式字符串在目标字符串的第一次出现的位置
比如
abababc
那么bab在其位置1处，bc在其位置5处
我们首先想到的最简单的办法就是蛮力的一个字符一个字符的匹配，但那样的时间复杂度会是O(m*n)
kmp算法保证了时间复杂度为O(m+n)

基本原理

举个例子：

发现x与c不同后，进行移动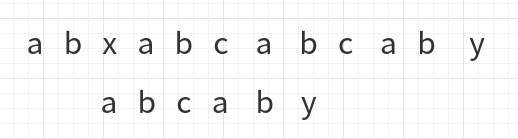

a与x不同，再次移动

此时比较到了c与y，
于是下一步移动成了下面这样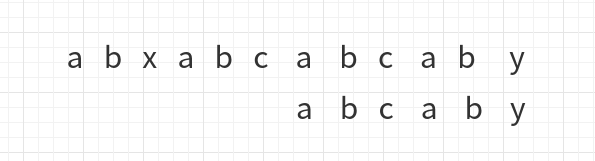

这一次的移动与前两次的移动不同，之前每次比较到上面长字符串的字符位置后，直接把模式字符串的首字符与它对齐，这次并没有，原因是这次移动之前，y与c对齐，但是y前边的ab是与自己的前缀ab一样，于是ab并不用再比较，直接从第三个位置开始比较，如图：

所以说kmp算法对于这种情况就直接使用当前比较字符之前的最长相同的前后缀，然后将前缀与上面的长字符串对齐，继续比较后面的字符串。
这里kmp算法中的一个重要点就来了，如何找到模式字符串中每位字符之前的最长相同前后缀呢
这里继续用一个例子举例：

下面的数字记录以该字符为结尾的最长前后缀相同子串的长度，先初始化为0,并且第一个字符下的数字确认为0
然后开始比较：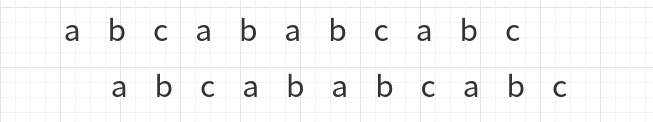

a与b不同，那么b下的数字也为0同理a与c不同，c下的数字也为0，接下来a与a对齐，如下

此时a与a相同，那么a下面的数字为1，也就是第二排字符串中当前比对的字符索引+1
接下来b与b相同，c与a不相同，那么此时上面的字符串不动，下面的字符串移动到当前比对位置即c的前一位的下方的数字的位置，如图：
移动前

c的前一位是b，b下方的数字是0，所以将下面字符串的第0位与之前的比对位置对其，即：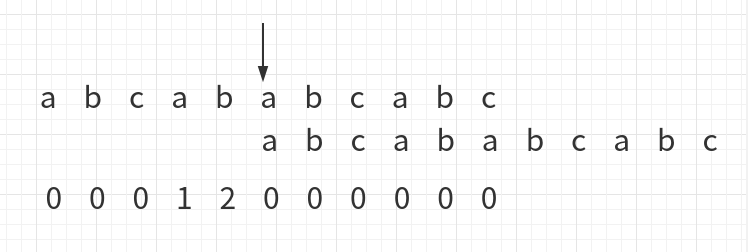

当前比对位置如箭头所示，然后继续向后比较，一直比到c与a：

此时c与a不相同，那么比较下面字符的前一个字符的下方数字的位置，如图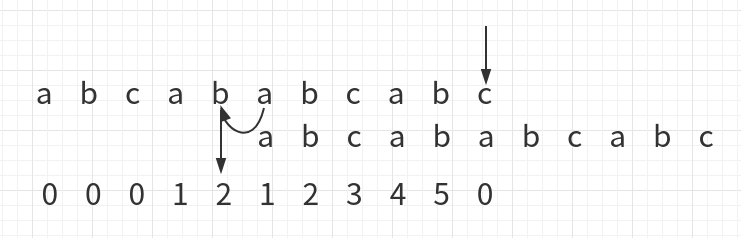

也就是位置为2的地方与上面比对位置对齐：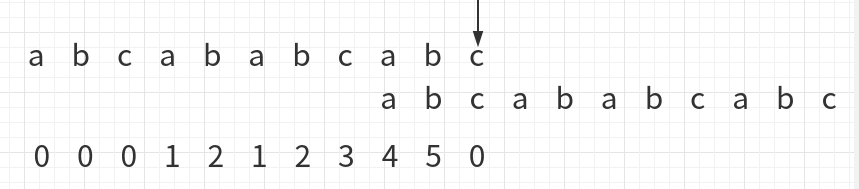

此时c与c相同，整个字符串自比对完成：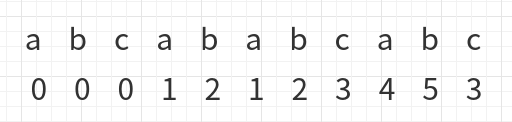

此时可能会没有理解为什么匹配不成功的时候要再比对其前一位字符下的数字的位置，那是因为这是要找到前一个字符位置下的最长相同前缀中的最长相同前缀，就举刚才的例子：

此时a前边是abcab，所以要找到abcab的最长相同前缀，就是ab，这时

然后再移动到ab与ab对其的位置继续比较即可

时间复杂度

简单来讲， 找到模式字符串中每位字符之前的最长相同前后缀的这个方法中，如果模式字符串的长度为m，那么上面的字符串的指向是一直向前移动的，下面字符串的整体也是一直向前移动的，最终移动的结果将会是长度为2m，所以比较次数也是最大为2m，时间复杂度为O(m)
kmp算法中，运用了找到模式字符串中每位字符之前的最长相同前后缀的这个方法的结果，然后使用类似的方法进行比较和移动，和上边的解释类似，如果这个要匹配的字符串长度为n，那最长的移动举例也超不过2n，所以总的时间复杂度为O(m+n)

具体代码

这里没有进行传入参数的验证，使用时还要注意。

def same_start_end(s):
    """最长前后缀相同的字符位数"""
    n = len(s) #整个字符串长度
    j = 0 # 前缀匹配指向
    i = 1 # 后缀匹配指向
    result_list=[0]*n
    while i < n:
        if j == 0 and s[j] != s[i]:  #　比较不相等并且此时比较的已经是第一个字符了
            result_list[i] = 0    # 值为０
            i += 1  # 向后移动
        elif s[j] != s[i] and j != 0: #比较不相等,将j值设置为ｊ前一位的result_list中的值，为了在之前匹配到的子串中找到最长相同前后缀
            j = result_list[j-1]
        elif s[j] == s[i]:   #相等则继续比较
            result_list[i] = j+1
            j = j+1
            i = i+1
    return result_list

def kmp(s,p):
    """kmp算法,s是字符串，p是模式字符串，返回值为匹配到的第一个字符串的第一个字符的索引，没匹配到返回-1"""
    s_length = len(s)
    p_length = len(p)
    i = 0  # 指向s
    j = 0  # 指向p
    next = same_start_end(p)
    while i < s_length:
        if s[i] == p[j]:  # 对应字符相同
            i += 1
            j += 1
            if j >= p_length:  # 完全匹配
                return i-p_length
        elif s[i] != p[j]:  # 不相同
            if j == 0:    # 与模式比较的是模式的第一个字符
                i += 1
            else:        # 取模式当前字符之前最长相同前后缀的前缀的后一个字符继续比较
                j = next[j]
    if i == s_length:    # 没有找到完全匹配的子串
        return -1

​