1.fdisk -l

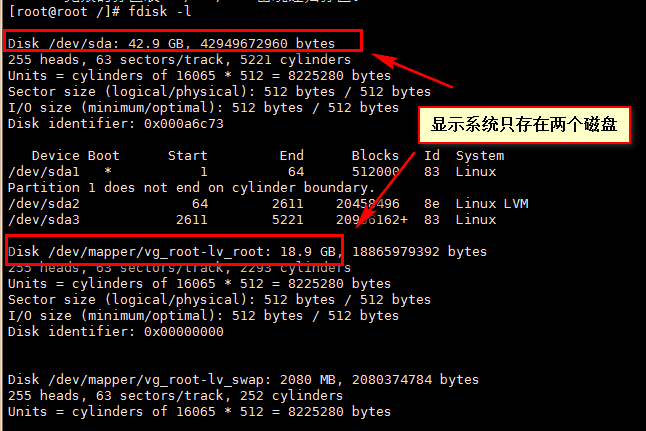
2.增加分区

3.3:键入 p，主分区，并键入3（编号）：

默认起始扇区和结束扇区即可(键入两次Enter) 键入t，修改分区类型为8e：

键入w，写分区表，然后重启：

卷扩容,添加进LVM组

查看卷组,并将初始化的分区加入到虚拟卷组
为卷组vg_root添加新的物理卷sda3增加卷组的容量
vgextend vg_root /dev/sda3

现在才能扩展逻辑卷的大小

lvextend -L +10G /dev/mapper/vg_root-lv_root

最后使用resizefs2命令重新加载逻辑卷的大小才能生效
resize2fs /dev/mapper/vg_root-lv_root
然后再次查看逻辑卷的大小

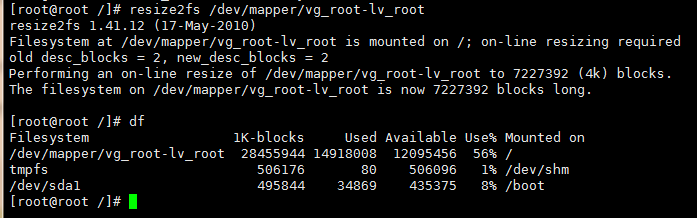
Linux记录-在线扩容8e的更多相关文章

  1. Linux LVM在线扩容

    环境: 虚拟化环境,SUSE Linux Enterprise Server 11sp3,直接把虚拟磁盘从100G改成150G. 现有的LVM是100G,/home 的LV需要再加50G. 步骤: f ...

  2. Linux lvm在线扩容

    1.查看磁盘空间 [root@bgd-mysql3 ~]# fdisk -l Disk /dev/sda: 107.4 GB, 107374182400 bytes, 209715200 sector ...

  3. Linux下lvm在线扩容步骤

    转 :https://jingyan.baidu.com/article/25648fc18f22b29191fd0011.html 图片看不清可以看原文 LVM是逻辑盘卷管理(Logical Vol ...

  4. 动态在线扩容root根分区大小的方法详解

    前言 本文主要介绍了关于动态在线扩容root根分区大小的相关内容,分享出来供大家参考学习,下面话不都说了,来一起看看详细的介绍吧. ? 1 qemu-img resize yourname.img + ...

  5. LVM在线扩容

    我虚拟机根分区已经使用了35%,现在需要对他进行在线扩容,扩容之后使用率降到30% [root@localhost ~]# dfFilesystem 1K-blocks Used Available ...

  6. 关于MySQL的在线扩容

    原文地址:http://bucketli.iteye.com/blog/1294032 主要简单总结下,mysql在线扩容和缩容一般涉及到的内容,主要包括三个方面,1.在线也就意味着需要把增量的数据重 ...

  7. Oracle VM VirtualBox虚拟机内Linux系统硬盘扩容步骤(CentOS6.5)

    1.首先获取要扩容的虚拟机的 UUID VBoxManage 改命令在C:\Program Files\Oracle\VirtualBox目录内,可先添加该目录到环境变量.C:\Users\yzkj- ...

  8. Linux磁盘空间扩容(LVM)

    Linux磁盘空间扩容(lvm) 随着系统的运行时间增长,业务数据的增长,原有磁盘的空间会存在空间不足情况,导致系统不能正常运行,或者系统管理员磁盘没有完全划完,根据使用者的需求自行划分.那么怎么才能 ...

  9. Linux中在线安装Mysql和修改密码设置服务启动

    一.说明:本文教大家在linux下在线安装mysql.网上的很多文章写的太乱,我们只取操作最方便的在线安装方式.本文以Centos为例. 二.安装过程. 1.安装客户端和服务端: (1)检查是否已经安 ...

随机推荐

  1. 读取CSV到DataTable

    using System; using System.Collections.Generic; using System.Data; using System.Data.OleDb; using Sy ...

  2. 异步、+回调机制、线程queue、线程Event、协程、单线程实现遇到IO切换

    # from concurrent.futures import ProcessPoolExecutor,ThreadPoolExecutor # import requests # import o ...

  3. springMVC整理05--数据校验、格式化 & 其他注解 & 数据绑定流程

    1.  数据校验.数据格式化 参考博客 http://www.importnew.com/19477.html 1.1  数据校验 使用 spring 数据校验,先要导入校验器的 jar: <! ...

  4. 「NOI2003」逃学的小孩

    传送门:>HERE< 题意:给出一棵树(带权),要从一个节点C先走到距离它近的一个节点B,再走到A,要求最坏情况下的总路程(即最长). 解题思路: 乍一看,A,B,C都没给出,这怎么求? ...

  5. HDU - 3917（朴素LIS + 最大流）

    题意: 求出所有的最长上升子序列的个数且每个元素只能用一次 解析: 呵...呵...呵..呵..emm... 再见 我死了...wa了15发之后...原来不能用~  要用 != EOF 这题算水题吧. ...

  6. SpringMVC的缓存对静态资源的影响 304 Not Modified

    我们知道在springmvc的配置中,可以添加缓存,但是缓存到底对静态资源有什么影响? 测试 没有添加缓存 <mvc:resources mapping="/image/**" ...

  7. [国家集训队]整数的lqp拆分

    我们的目标是求$\sum\prod_{i=1}^m F_{a_i}$ 设$f(i) = \sum\prod_{j=1}^i F_{a_j}$那么$f(i - 1) = \sum\prod_{j=1}^ ...

  8. 洛谷P5069 [Ynoi2015]纵使日薄西山（树状数组，set）

    洛谷题目传送门 一血祭 向dllxl致敬! 算是YNOI中比较清新的吧,毕竟代码只有1.25k. 首先我们对着题意模拟,寻找一些思路. 每次选了一个最大的数后,它和它周围两个数都要减一.这样无论如何, ...

  9. NOIP引水入城（dfs）

    为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施.水利设施有两种,分别为蓄水厂和输水站.蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中. 因此,只有与湖泊毗邻的第1 行的 ...

  10. 对于Spring中注入对象失败的问题

    1.今天进行了一段代码,经过检查发现config配置文件没问题,注入注解也编写正确,但是RedisTemplate就是会抛出空指针异常. 进过一系列检查发现,其在用户使用该类的时候采用的是new方式创 ...