LOJ#2353 货币兑换

CDQ分治优化斜率优化DP。

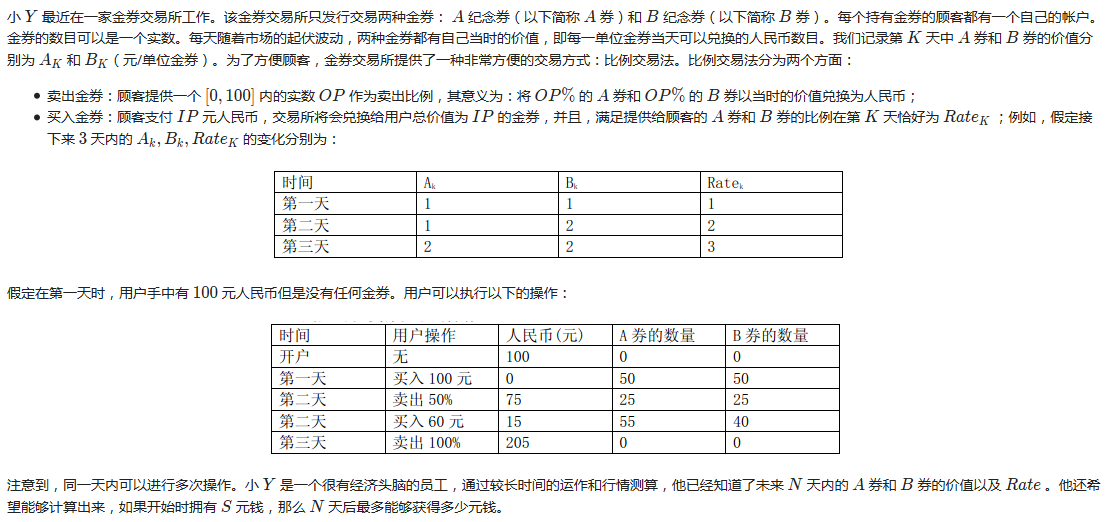
有个结论就是每天买完卖完....知道这个之后考虑今天卖的是哪天买的就能写出n²DP了。

发现形式是f_i = max(a_ib_j + c_id_j)的形式。我们可以把c_i除出来，就是斜率优化了。

然后发现横坐标和斜率全部没有单调性，于是CDQ分治搞一搞。

 #include <bits/stdc++.h>

 const int N = ;
 const long double eps = 1e-;

 long double a[N], b[N], c[N], R[N], f[N], s, k[N], v[N], w[N];
 int n, node[N], t[N], stk[N], top;

 template <class T> inline void Max(T &a, const T &b) {
     a < b ? a = b : ;
     return;
 }

 inline bool cmp_k(const int &a, const int &b) {
     return k[a] < k[b];
 }

 inline bool cmp_w(const int &a, const int &b) {
     return w[a] < w[b];
 }

 inline bool check(int a, int b, int c) {
     if((v[b] - v[a]) * (w[c] - w[b]) + eps >= (v[c] - v[b]) * (w[b] - w[a])) {
         return ;
     }
     return ;
 }

 void CDQ(int l, int r) {

     //printf("CDQ : l = %d r = %d \n", l, r);

     if(l == r) {
         if(r > ) f[r] *= b[r];
         Max(f[r], f[r - ]);
         v[r] = -f[r] / c[r];
         w[r] = -v[r] * R[r];
         //std::cout << "v[i] = " << v[r] << std::endl;
         //printf("f = %.3f \n", f[r]);
         return;
     }
     int mid = (l + r) >> ;
     CDQ(l, mid);

     /// update
     memcpy(t + l, node + l, (r - l + ) * sizeof(int));
     std::sort(t + l, t + mid + , cmp_w);
     std::sort(t + mid + , t + r + , cmp_k);
     // build convex
     stk[top = ] = t[l];
     if(mid - l +  >= ){
         stk[++top] = t[l + ];
         for(int i = l + ; i <= mid; i++) {
             while(top >  && check(stk[top - ], stk[top], t[i])) {
                 top--;
             }
             stk[++top] = t[i];
         }
     }
     // update f
     //printf("top = %d \n", top);
     int head = ;
     for(int i = mid + ; i <= r; i++) {
         int x = t[i];
         while(head < top && (v[stk[head]] - v[stk[head + ]]) / (w[stk[head]] - w[stk[head + ]]) + eps < k[x]) {
             head++;
         }
         int y = stk[head];
         //printf("Max %.3f  %.3f * %.3f \n", f[x], -v[y], (R[y] * a[x] + b[x]));
         //Max(f[x], -v[y] * (R[y] * a[x] + b[x]));
         Max(f[x], w[y] * k[x] - v[y]);
     }

     CDQ(mid + , r);
     return;
 }

 int main() {

     //freopen("in.in", "r", stdin);
     //freopen("my.out", "w", stdout);

     scanf("%d%Lf", &n, &s);
     for(int i = ; i <= n; i++) {
         scanf("%Lf%Lf%Lf", &a[i], &b[i], &R[i]);
         c[i] = a[i] * R[i] + b[i];
         //std::cout << "c[i] = " << c[i] << std::endl;
         k[i] = a[i] / b[i];
         node[i] = i;
     }

     f[] = s;

     CDQ(, n);

     printf("%.3Lf\n", f[n]);
     return ;
 }

AC代码

eps很重要...