映射&集合

哈希函数

通过哈希表可以实现 O(1) 复杂度的查找。

哈希函数构造方法：设计好的哈希函数的两个基本原则，计算简单+分布均匀

1. 直接定址法

　　用key自身的某个线性函数来定址，f(key) = a*key + b。但需要知道关键字的分布情况。

2. 数字分析法

　　适合处理关键字位数比较大的情况。抽取关键字的一部分作为哈希地址。

3. 平方取中法

　　将key平方后取中间若干位数字作为哈希地址。

4. 折叠法

　　将key分为位数相等的几个部分，将这几部分叠加求和，按哈希表表长取后几位作为哈希地址。

5. 除留余数法

　　最常用。对哈希表长为m，f(key) = key mod p ，p小于等于m。p的选择非常重要，选的不好可能造成哈希冲突。

处理哈希冲突的方法：key1 != key2 但 f(key1) == f(key2)，哈希冲突。

1. 开放定址法：一旦发生冲突，就去找下一个空的哈希地址，只要哈希表足够大，总能找到空的哈希地址。

　　fi(key) = (f(key)+di) mod p，di = 1, 2, ..., p-1     线性探测法。

　　直接这样取值di比较盲目，可以通过修改di的取值方式，例如平方运算，来尽量解决堆积问题，二次探测法。

　　fi(key) = (f(key)+di) mod p，di = 1², -1², 2², -2² , ..., q², -q² ；q<=p/2

　　或者直接用随机函数来取值di，称之为随机探测法。

　　fi(key) = (f(key)+di) mod p，di是由随机函数产生的序列。

2. 再哈希函数法，准备多个哈希函数，当出现冲突的时候，调用下一个哈希函数进行计算。最后还是出现冲突的可能很低。

3. 链地址法（拉链法），常用方法。利用单链表，哈希表存的不是记录元素，而是记录的地址，如果出现冲突，就从前面的记录再链到冲突的元素即可。

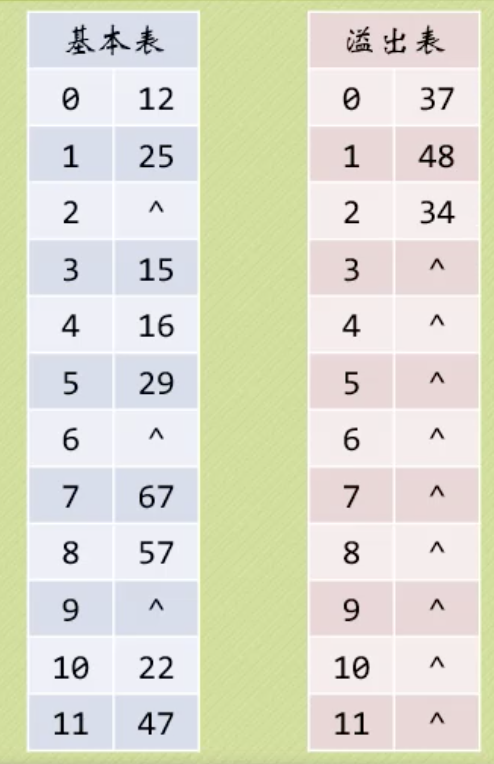
4. 公共溢出区法，对于冲突的记录单独用溢出表连续存储，如果哈希搜索不到，就去溢出区中找。对于一个比较优秀的哈希函数，这种方法解决冲突的效率较高。

List：实现方式可以是数组也可以是链表，元素可重复。插入O(1)，查找O(n)。

Map：key-value对构成，键key不重复。

Set：不允许有重复元素。用哈希表（或二叉树）来实现，所以查找O(1) 复杂度（或O(logn)）。

用哈希表实现，元素排列乱序，查找O(1)；用二叉搜索树实现，元素排列相对有序，查找O(logn)。

各语言中的 hashmap ：

各语言中的 hashset：