python机器学习——逻辑回归

我们知道感知器算法对于不能完全线性分割的数据是无能为力的，在这一篇将会介绍另一种非常有效的二分类模型——逻辑回归。在分类任务中，它被广泛使用

逻辑回归是一个分类模型，在实现之前我们先介绍几个概念：

几率（odds ratio）：
\[
\frac {p}{(1-p)}
\]
其中p表示样本为正例的概率，当然是我们来定义正例是什么，比如我们要预测某种疾病的发生概率，那么我们将患病的样本记为正例，不患病的样本记为负例。为了解释清楚逻辑回归的原理，我们先介绍几个概念。

我们定义对数几率函数（logit function）为：
\[
logit(p) = log \frac {p}{(1-p)}
\]
对数几率函数的自变量p取值范围为0-1，通过函数将其转化到整个实数范围中，我们使用它来定义一个特征值和对数几率之间的线性关系为：
\[
logit(p(y=1|x)) = w_0x_0+w_1x_1+...+w_mx_m = \sum_i^nw_ix_i=w^Tx
\]
在这里，p(y=1|x)是某个样本属于类别1的条件概率。我们关心的是某个样本属于某个类别的概率，刚好是对数几率函数的反函数，我们称这个反函数为逻辑函数（logistics function），有时简写为sigmoid函数：
\[
\phi(z) = \frac{1}{1+e^{-z}}
\]
其中z是权重向量w和输入向量x的线性组合：
\[
z = w^Tx=w_0+w_1x_1+...+w_mx_m
\]
现在我们画出这个函数图像：

import matplotlib.pyplot as plt

import numpy as np

def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

z = np.arange(-7, 7, 0.1)

phi_z = sigmoid(z)

plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.axhspan(0.0, 1.0, facecolor='1.0', alpha=1.0, ls='dotted')
plt.yticks([0.0, 0.5, 1.0])
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.show()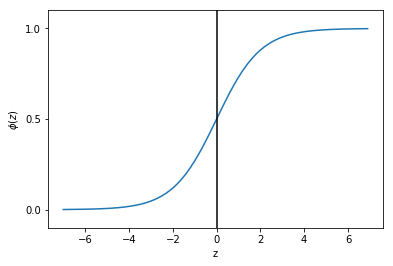

可以看出当z接近于正无穷大时，函数值接近1，同样当z接近于负无穷大时，函数值接近0。所以我们知道sigmoid函数将一个实数输入转化为一个范围为0-1的一个输出。

我们将逻辑函数将我们之前学过的Adaline联系起来，在Adaline中，我们的激活函数的函数值与输入值相同，而在逻辑函数中，激活函数为sigmoid函数。

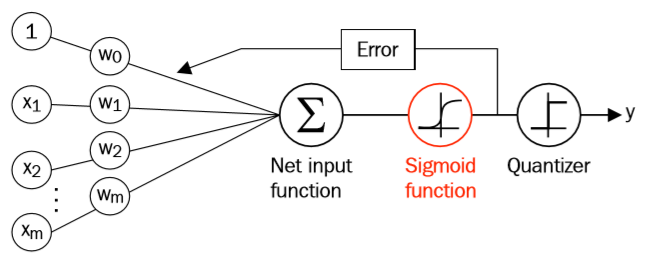
sigmoid函数的输出被解释为某个样本属于类别1的概率，用公式表示为：
\[
\hat y=\begin{cases}1,\quad \phi(z)\ge 0.5 \\\\0,\quad otherwise\end{cases}
\]
也就是当函数值大于0.5时，表示某个样本属于类别1的概率大于0.5，于是我们就将此样本预测为类别1，否则为类别0。我们仔细观察上面的sigmoid函数图像，上式也等价于：
\[
\hat y=\begin{cases}1,\quad z\ge 0.0 \\\\0,\quad otherwise\end{cases}
\]
逻辑回归的受欢迎之处就在于它可以预测发生某件事的概率，而不是预测这件事情是否发生。

我们已经介绍了逻辑回归如何预测类别概率，接下来我们来看看逻辑回归如何更新权重参数w。

对于Adaline，我们的损失函数为：
\[
J(w) = \sum_i\frac12(\phi(z^{(i)})-y^{(i)})^2
\]
我们通过最小化这个损失函数来更新权重w。为了解释我们如何得到逻辑回归的损失函数，在构建逻辑回归模型时我们要最大化似然L（假设数据集中的所有样本都是互相独立的）：
\[
L(w)=P(y|x,w)=\prod^n_{i=1}P(y^{(i)}|x^{(i)};w)=\prod^n_{i=1}(\phi(z^{(i)}))^{y^{(i)}}(1-\phi(z^{(i)}))^{1-y^{(i)}}
\]
通常我们会最大化L的log形式，我们称之为对数似然函数：
\[
l(w)=logL(w)=\sum_{i=1}^n\left[y^{(i)}log(\phi(z^{(i)})+(1-y^{(i)})log(1-\phi(z^{(i)}))\right]
\]
这样做有两个好处，一是当似然很小时，取对数减小了数字下溢的可能性，二是取对数后将乘法转化为了加法，可以更容易的得到函数的导数。现在我们可以使用一个梯度下降法来最大化对数似然函数，我们将上面的对数似然函数转化为求最小值的损失函数J：
\[
J(w)=\sum_{i=1}^n\left[-y^{(i)}log(\phi(z^{(i)}))-(1-y^{(i)})log(1-\phi(z^{(i)}))\right]
\]
为了更清晰的理解上式，我们假设对一个样本计算它的损失函数：
\[
J(\phi(z),y;w)=-ylog(\phi(z))-(1-y)log(1-\phi(z))
\]
可以看出，当y=0时，式子的第一部分为0，当y=1时，式子的第二部分为0，也就是：
\[
J(\phi(z),y;w)=\begin{cases}-log(\phi(z)),\quad if\ y=1 \\\\-log(1-\phi(z)),\quad if \ y=0\end{cases}
\]

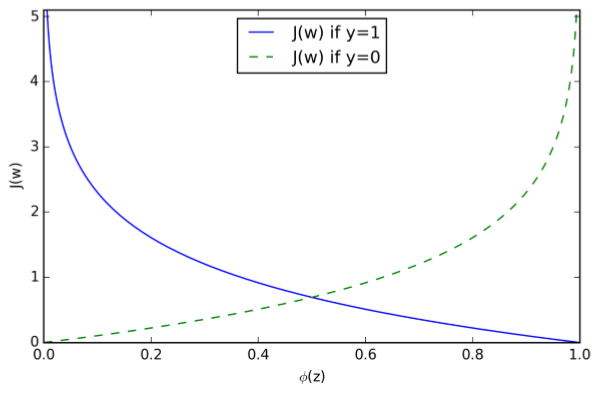
可以看出，当我们预测样本所属于的类别时，当预测类别是样本真实类别的概率越大时，损失越接近0，而当预测类别是真实类别的概率越小时，损失越接近无穷大。

作为举例，我们这里对权重向量w中的一个分量进行更新，首先我们求此分量的偏导数：
\[
\frac{\partial }{\partial w_j}l(w) = \left(y\frac{1}{\phi(z)}-(1-y)\frac{1}{1-\phi(z)}\right)\frac{\partial }{\partial w_j}\phi(z)
\]
在继续下去之前，我们先计算一下sigmoid函数的偏导数：
\[
\frac{\partial }{\partial z}\phi(z) = \frac{\partial }{\partial z}\frac{1}{1+e^{-z}}=\frac{1}{(1+e^{-z})^2}e^{-z}=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})\\=\phi(z)(1-\phi(z))
\]
现在我们继续：
\[
\left(y\frac{1}{\phi(z)}-(1-y)\frac{1}{1-\phi(z)}\right)\frac{\partial }{\partial w_j}\phi(z)\\=\left(y\frac{1}{\phi(z)}-(1-y)\frac{1}{1-\phi(z)}\right)\phi(z)(1-\phi(z))\frac{\partial }{\partial w_j}z\\=\left(y(1-\phi(z))-(1-y)\phi(z)\right)x_j\\=(y-\phi(z))x_j
\]
所以我们的更新规则为：
\[
w_j = w_j + \eta\sum^n_{i=1}\left(y^{(i)}-\phi(z^{(i)})\right)x_j^{(i)}
\]
因为我们要同时更新权重向量w的所有分量，所以我们更新规则为（此处w为向量）：
\[
w = w+\Delta w\\\Delta w = \eta\nabla l(w)
\]
因为最大化对数似然函数也就等价于最小化损失函数J，于是梯度下降更新规则为：
\[
\Delta w_j=-\eta\frac{\partial J}{\partial w_j}=\eta\sum^n_{i=1}\left(y^{(i)}-\phi(z^{(i)})\right)x^{(i)}_j\\w=w+\Delta w,\Delta w=-\eta \nabla J(w)
\]