关键路径法(Critical Path Method, CPM)

1、活动节点描述及计算公式

通过分析项目过程中哪个活动序列进度安排的总时差最少来预测项目工期的网络分析。

产生目的：为了解决，在庞大而复杂的项目中，如何合理而有效地组织人力、物力和财力，使之在有限资源下以最短的时间和最低的成本费用下完成整个项目。
关键路径是相对的，也可以是变化的。

关键路径可以有多条，关键路径上的活动时差为0。

活动节点图如下：

ES：最早开始时间(Earliest Start)，是指某项活动能够开始的最早时间，只决定于项目计划，只要计划的条件满足了就可以开始的时间。

EF：最早结束时间(Earliest Finish)，是指某项活动能够完成的最早时间。其中EF = ES+DU， DU为活动持续时间，顺推法先知道开始时间。

LF：最迟结束时间(Latest Finish)，是指为了使项目在要求完工时间内完成，某项活动必须完成的最迟时间。往往决定于相关方（客户或管理层）的限制。

LS：最迟开始时间(Latest Start)，是指为了使项目在要求完工时间内完成，某项活动必须开始的最迟时间。其中LS = LF -DU，DU为持续时间，逆推法先知道结束时间。

顺推法：

1、任一活动的最早开始时间，等于所有前置活动的最早结束时间的最大者;

2、任一活动的最早结束时间，等于该活动的最早开始时间 + 该活动工期 ;

3、 没有前置活动的，ES等于项目的开始时间。

EF = ES + DU

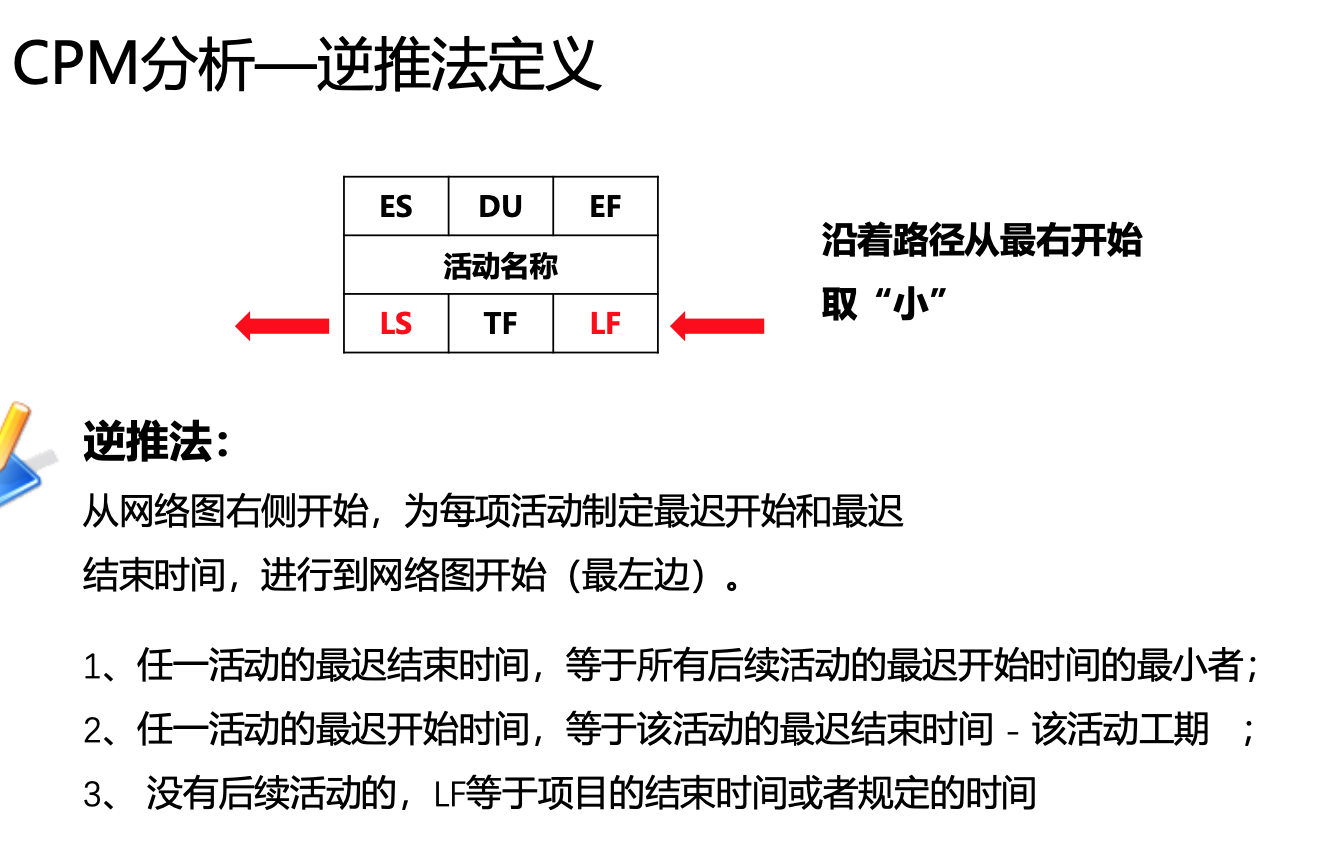
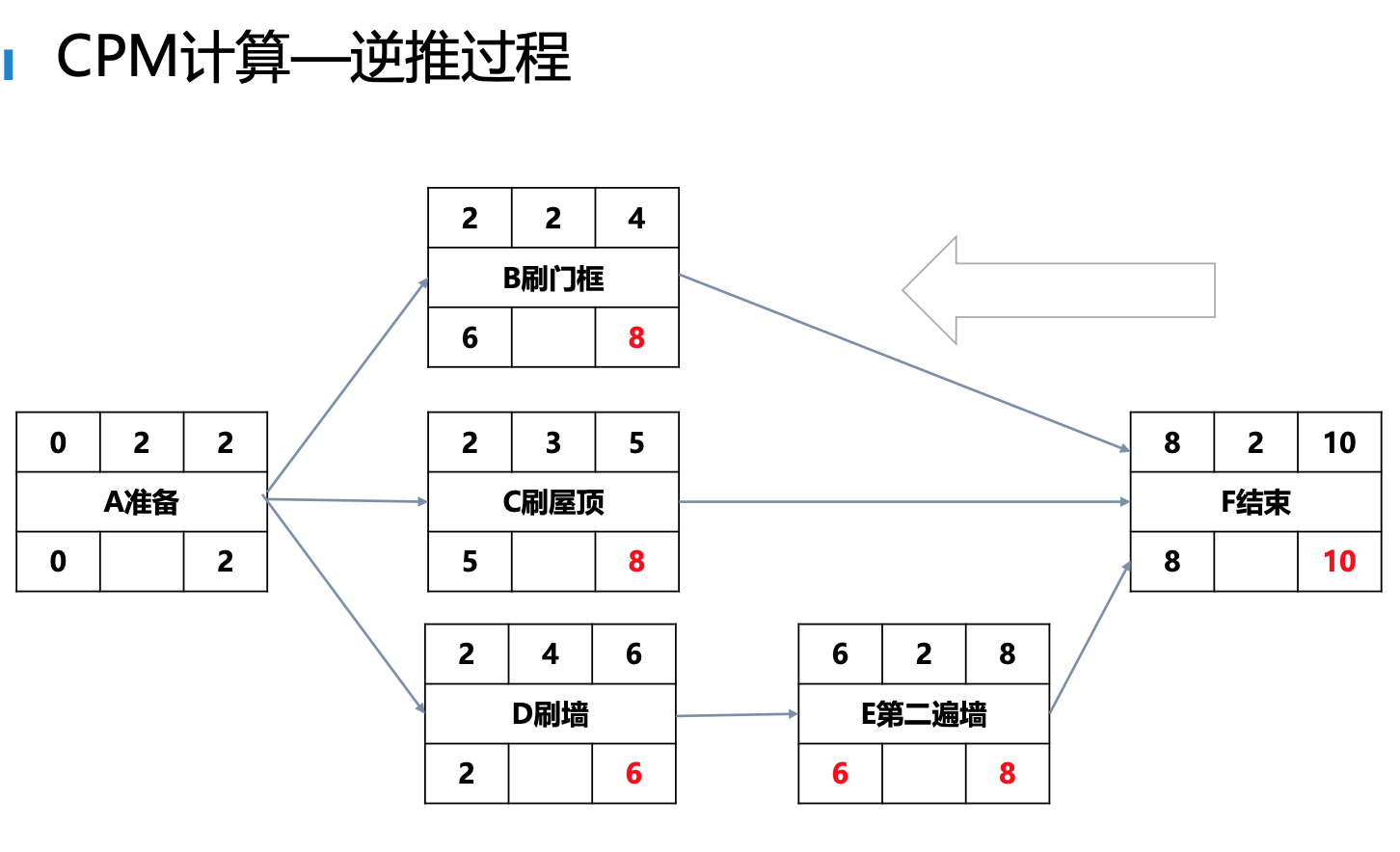
逆推法：

从网络图右侧开始，为每项活动制定最迟开始和最迟 结束时间，进行到网络图开始(最左边)。

1、任一活动的最迟结束时间，等于所有后续活动的最迟开始时间的最小者;

2、任一活动的最迟开始时间，等于该活动的最迟结束时间 - 该活动工期 ;

3、 没有后续活动的，LF等于项目的结束时间或者规定的时间。

LS = LF - DU

总浮动时间：

TF = LF – EF 或者 LS- ES ，活动在TF之间推迟不影响总工期(注意如果超 出该TF，则关键路径将发生变化)，TF为0的路径为CP(关键路径)自由时差FF = 紧后ES - EF，活动在FF内推迟不影响紧后活动。

4. 活动从第0天开始还是从第1天开始

采用顺推法和逆推法进行进度网络路径计算时，需要关注活动是从第0天开始还是从第1天开始，不同的假设计算的结果是不一样的。首先需要明确以下几个概念。

• 活动的持续时间DU是指活动的工作时间段，例如一个活动持续时间是24小时，是指3个工作日（每天8小时）。

• 活动的开始时间是指活动开工日的上班开始时间；活动结束是指开工日的下班时间。也就是说假设一个活动的持续时间是2天，是指从第1天上班时间，到第2天下班时间的所有工作时间段。

所谓活动从第0天还是第1天开始，意思是说要不要把活动开始的那一天计算在工作时间段内。因为现实中第0天是不存在的，所以活动开始的那一天就不需要计算在内；而活动从第1天开始，由于第1天是存在的，就需要计算在工作时间段内。这两种情况导致当前活动的EF或者LS，紧后活动的ES和LF在计算时要考虑是否减去或加上这1天的问题。

无论是从第0天开始，还是第1天开始，都不会影响关键路径的和浮动时间的计算方法，但是考试中如果弄错了则会影响计算结果，考试中为了简化计算通常采用第0天开始，现实中为了与实际相符合通常采用第1天开始。下面就这两种方式举例说明。

　　　　　　　　　　　　

图6-25

第一种情况：活动从第0天开始。如图6-25

计算公式如下：

（1） 对于当前活动：

• 顺推时 EF  = ES + DU；

• 逆推时 LS=  LF – DU

 

（2）对于紧后活动：

 

• 顺推时ES_i= EF_i-1,；

• 逆推时LF_i-1 = LS _i  （例如逆推时活动C相当于活动D的紧后活动）

其中自左向右，“i”代表当前活动，则“i-1”代表“i”的紧前活动。

例如：对于活动A、B的最早时间：

• EF_A= ES_A+DU = 0+5 = 5，

• ES_B = EF_A= 5；

对于活动D和C的最晚时间：

• LS_D= LF_D – DU = 30 -15 =15，

• LF_C = LS_D= 15；

第二种情况：活动从第1天开始。如图6-26

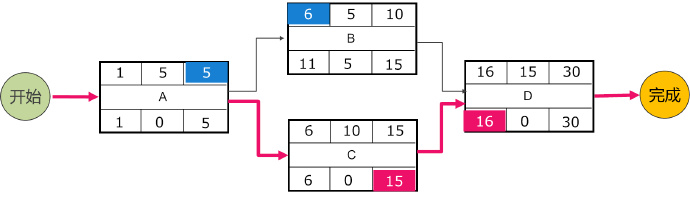
图6-26

 

对于当前活动

 

• 顺推时 EF  = （ES + DU）-1； 

• 逆推时 LS =（LF – DU）+1

 

对于紧后活动

 

• 顺推时ES_i= EF_i-1 +1；

• 逆推时LF_i-1 = LS _i -1

其中自左向右，“i”代表当前活动，则“i-1”代表“i”的紧前活动。例如：

对于活动A、B的最早时间：

• EF_A= ES_A+DU-1 = 1+5-1 = 5，

• ES_B = EF_A+1= 5+1 = 6；

对于活动D和C的最晚时间：

• LS_D= LF_D – DU+1 = 30 -15 +1 =16，

• LF_C =LS_D -1 = 15；

@提示：从上两种计算方法来看，活动从第0天开始显然对人工计算来说更加直观简便，这种方法的缺点是与日历日期的对应关系是不一致的。活动从第1天开始计算的结果与日历日期是一致的，但是计算过程是不直观的。好在考试中一般不会涉及具体的日历日期，所以推荐使用活动从第0天开始的计算方法。

二：