B-Quadratic equation_2019牛客暑期多校训练营（第九场）

题意

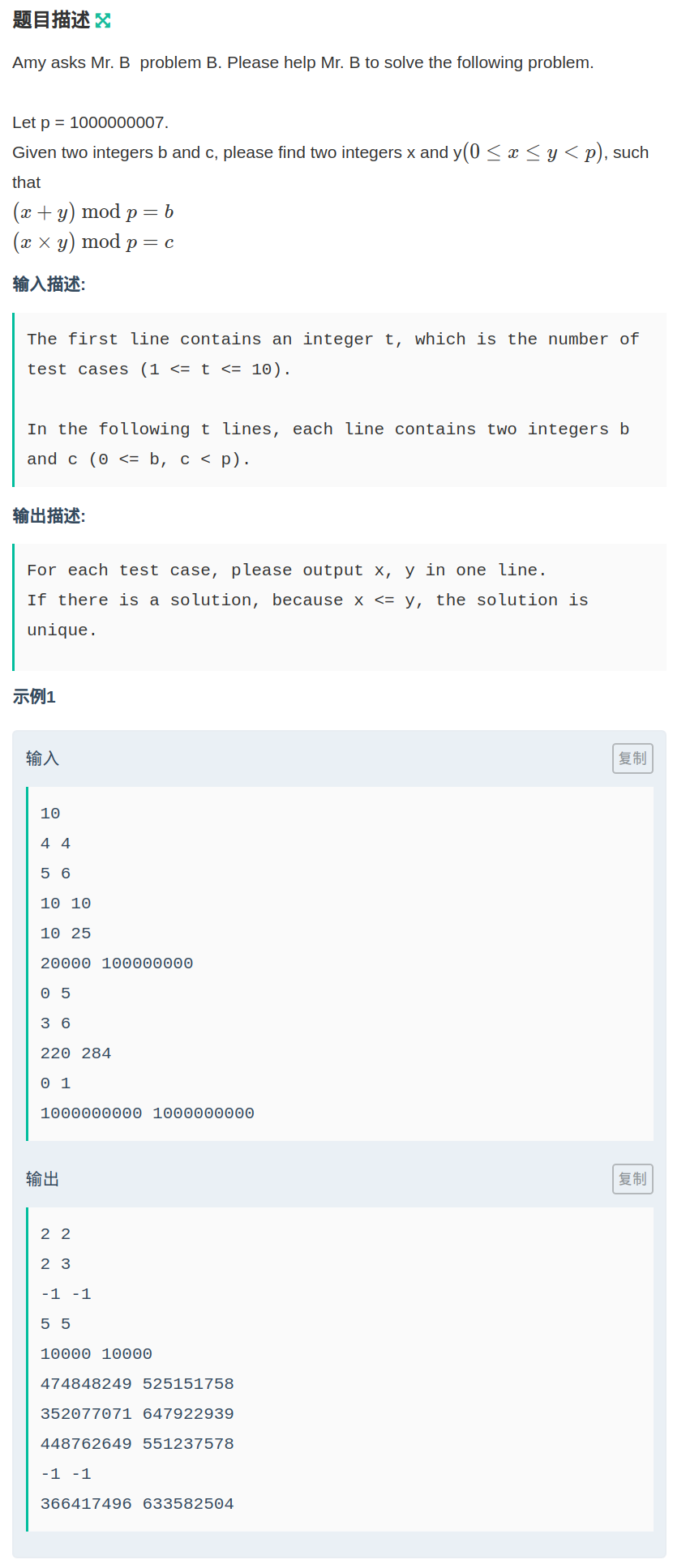
解下列方程

\((x+y) \equiv b \ mod \ p\)

\((x\ *\ y) \equiv c \ mod \ p\)

题解

\(y = b-x\) 带入二式

\(x * (b-x) \equiv c \ mod \ p\)

\(bx - x^2 =c + kp\)

\(x^2 - bx + c + kp = 0\)

解得\(x = \frac{b \ \pm \ \sqrt{b^2 - 4c+kp} }{2}\)

要使\(x\)为整数则\(\sqrt{b^2 - 4c+kp}\)要为整数

令\(z = \sqrt{b^2 - 4c+kp}\)

\(z^2 = b^2 - 4c+kp\)

\(z^2 \equiv \ b^2 - 4c \ mod \ p\)

问题就变成了二次剩余

先判断是否有解也就是\(b^2-4c\)是否是\(p\)的二次剩余

利用欧拉准则：当且仅当\(d^{\frac{p-1}{2}} \equiv 1 \ mod \ p\)，\(d\)为\(p\)的二次剩余

当且仅当\(d^{\frac{p-1}{2}} \equiv -1 \ mod \ p\)，\(d\)为\(p\)的非二次剩余

接下来套二次剩余板子求\(z\)即可，有一种特殊情况当\(p \ \% \ 4 = 3\)时可以用公式\(z = d^{\frac{p+1}{4}} \% \ p\)快速求解

现在\(x = \frac{b + z}{2}, y = \frac{b - z}{2}\)，可能不是整数，我们对x和y都乘上一个偶数(p+1)就可以保证x，y是整数且仍然满足题目的两个方程，因为

\((x+y)*(p+1) \ \%\ p =(x+y) \% p\ *\ (p+1) \% p = b*1 = b\)

\(x*(p+1)*y*(p+1)\%p = (x*y)\%p\ *\ (p^2+2p+1)\%p = c*1 = c\)

*顺带扒了一下咖啡鸡的板子

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const ll mod = 1e9+7;

ll pow_mod(ll a, ll b) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b /= 2;
    }
    return ans;
}

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        ll b, c;
        scanf("%lld%lld", &b, &c);
        ll t = ((b*b - 4*c) % mod + mod) % mod;
        if (pow_mod(t, (mod-1)/2) == mod-1) puts("-1 -1");
        else {
            ll z = pow_mod(t, (mod+1)/4);
            ll x = ((b + z) % mod + mod) % mod;
            ll y = ((b - z) % mod + mod) % mod;
            x = x * (mod+1) / 2 % mod;
            y = y * (mod+1) / 2 % mod;
            if (x > y) swap(x, y);
            printf("%lld %lld\n", x, y);
        }
    }
    return 0;
}

二次剩余模板

//调用solve(d, p)返回x
mt19937_64 gen(time(0));
struct T{ll x,y;};
ll w;
T mul_two(T a,T b,ll p){
    T ans;
    ans.x=(a.x*b.x%p+a.y*b.y%p*w%p)%p;
    ans.y=(a.x*b.y%p+a.y*b.x%p)%p;
    return ans;
}

T qpow_two(T a,ll n,ll p){
    T ans;
    ans.x=1;
    ans.y=0;
    while(n){
        if(n&1) ans=mul_two(ans,a,p);
        n>>=1;
        a=mul_two(a,a,p);
    }
    return ans;
}

ll qpow(ll a,ll n,ll p){
    ll ans=1;
    a%=p;
    while(n){
        if(n&1) ans=ans*a%p;
        n>>=1;
        a=a*a%p;
    }
    return ans%p;
}

ll Legendre(ll a,ll p){
    return qpow(a,(p-1)>>1,p);
}

int solve(ll n,ll p){
    if (n==0) return 0;
    if (n==1) return 1;
    if(Legendre(n,p)+1==p) return -1;
    ll a,t;
    while(1){
        a=gen()%p;
        t=a*a-n;
        w=(t%p+p)%p;
        if(Legendre(w,p)+1==p) break;
    }
    T tmp;
    tmp.x=a;
    tmp.y=1;
    T ans=qpow_two(tmp,(p+1)>>1,p);
    return ans.x;
}