AVLTree的Python实现
AVLTree
自己最近在学习数据结构，花了几天理解了下AVLTree的实现，简单一句话概括就是先理解什么是旋转，然后弄明白平衡因子在各种旋转后是如何变化的。最后整理了下学习的过程，并尽量用图片解释，代码水平请高手看到别笑话，有逻辑错误也欢迎指出，谢谢。
简单目录结构:
介绍:
AVL树称为自平衡二叉查找树, 也称为高度平衡二叉搜索树。与普通的二叉搜索树(BST)相比，它能尽量保持子树的高度差不超过2，以减少搜索的时间。
相关概念:
树的高度: 高度是指树节点的最大层次。
AVL树的高度差: 是指在avl树中，任意子树的左右节点的高度差不能超过1
平衡因子: blance factor(bf)指代某个节点左右子树的高度差，即左子树减去右子树的高度，值区间为[-1,0,1]。
搜索效率: AVL树的插入删除查找时间复杂度都为log2N
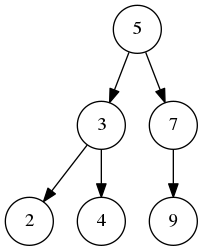
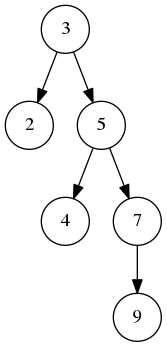
AVL树 BST树
插入实现细节
介绍插入之前先说明每个节点的定义:
class Node(object):
def __init__(self, key, parent=None, left=None, right=None):
self.key = key # 存储的数据
self.parent = parent # 父节点
self.left = left # 左孩子节点
self.right = right # 右孩子节点
self.bf = 0 # 平衡因子 等于左子树高度减去右子树高度
旋转
旋转是AVL树最重要的操作了，理解了旋转就理解了AVL树的实现原理。
左单旋转
下图节点上面的数字表示平衡因子
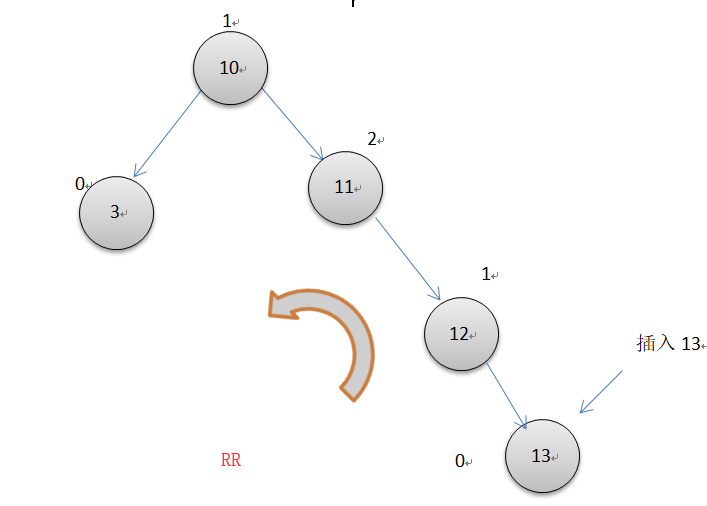
如上图所示: 插入13后，右边子树11节点的平衡因子变为了2(左右节点的高度差), 整个avl树开始不平衡，这时便要开始以12为轴心进行一次左单旋转。具体旋转的操作是原来11的父节点10指向12,12的左节点指向11，而11的右节点指向原来12的左节点（此例中，12的左节点为空）。
说明一下自己对左旋转后，主要操作的两个节点12和11的平衡因子为啥一定是0的理解。
假设原来12节点的左子节点的高度为a, 那么根据平衡因子为1可知，12的右子节点高度为a+1，11的右子节点高度为a+2，此时11的左子节点高度则为a， 发生左单旋转后，11的左子节点高度没变仍为a，11的右子节点指向了原来的12的左子节点，高度为a，所以11的平衡因子则为0，而12的平衡因子等于左边子树1+节点11的高度a减去12的右子节点高度a+1，所以12平衡因子也为0。
def l_rotate(self, par, cur):
"""
左单旋转
:param par: 平衡因子为2|-2的节点
:param cur: 作为轴心旋转的节点(平衡因子不为2)
:return: None
"""
p = cur.left # 辅助引用p指向cur的左节点
cur.left = par # cur的左节点指向par
par.right = p # par的右节点指向cur的左节点
if p:
p.parent = par # cur的左节点不为空时更新该节点的父节点
if par == self.root:
self.root = cur # 判断平衡因子为2的par是否为根
else:
if par == par.parent.left: # 更新par父节点的子节点信息
par.parent.left = cur
else:
par.parent.right = cur
cur.parent = par.parent # 当前cur的父节点指向原来par的父节点
par.parent = cur # par变为cur的左子节点
cur.bf = par.bf = 0 # 插入操作中, 操作的两个节点旋转后平衡因子恢复为0
右单旋转
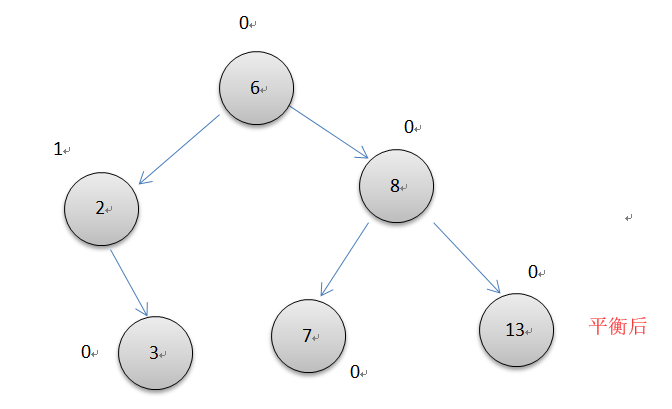
上图中插入3后左子树不平衡了，根节点8的平衡因子变为了-2, 此时应该以6为轴心向右单旋转一次，具体操作与左单旋转类似：8的左节点指向6的左节点（此时为7），6的右节点指向8，由于8原来是根节点，没有父节点，所以根节点指向6。旋转后6和8节点都恢复0的平衡因子了。代码如下，与左单循环基本一样。
def r_rotate(self, par, cur):
"""右单旋转"""
p = cur.right
cur.right = par
par.left = p
if p:
p.parent = par
if par == self.root:
self.root = cur
else:
if par == par.parent.left:
par.parent.left = cur
else:
par.parent.right = cur cur.parent = par.parent # 更新父节点信息
par.parent = cur
cur.bf = par.bf = 0 # 更新平衡因子
左右双旋转
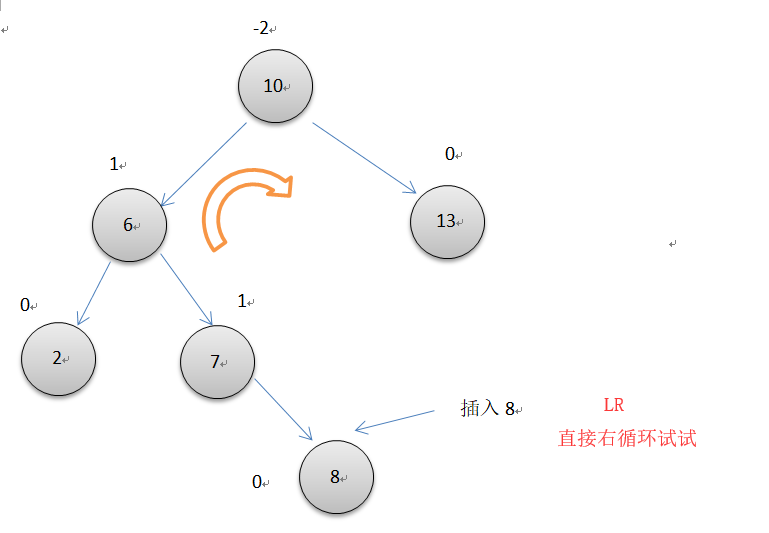
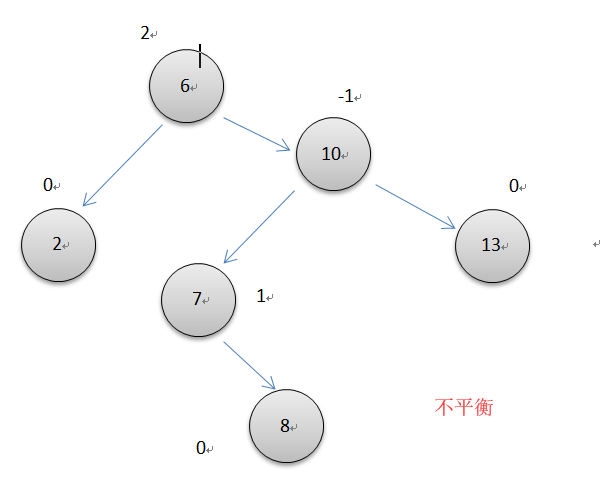
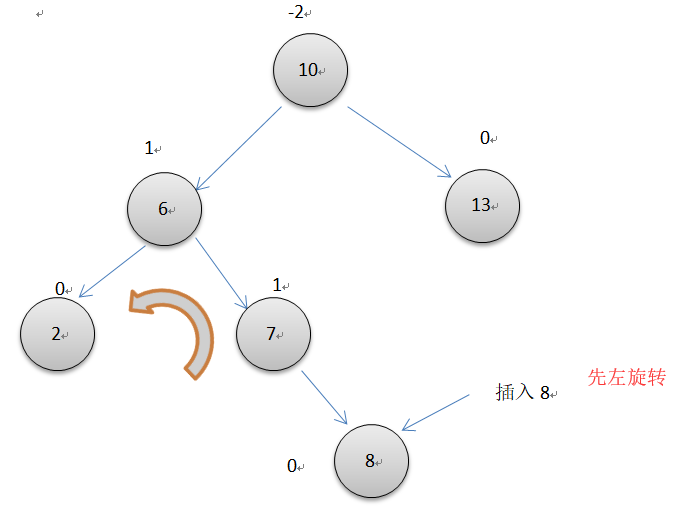
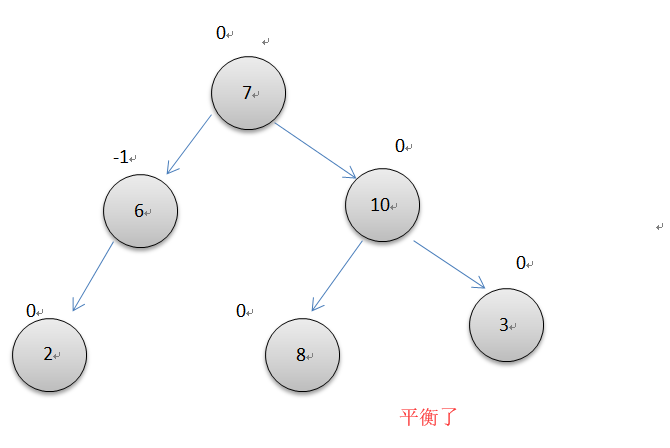
如上图所示，10节点的平衡因子为-2，而它的左节点的平衡因子却为1，两个节点失去平衡的方向不一样，所以要先以7位轴心对节点6左单旋转一次，再以7为轴心对节点10右旋转一次。操作细节和同上面单次循环一样。注意此时操作的3个节点的平衡因子要根据不同7的平衡因子单独调整。代码很简单，利用已经写好的左右单旋转即可完成。
def lr_rotate(self, par, cur):
"""左右双旋转"""
# 先左旋转 cur 和 cur的右子节点
cur_right = cur.right # 获得cur的右子节点的引用
bf = cur_right.bf
self.l_rotate(cur, cur_right)
# 继续右旋转
self.r_rotate(par, cur_right)
if bf == 0: # 根据cur_right的平衡因子更新操作的3个节点
cur.bf = cur_right.bf = par.bf = 0
elif bf == -1:
par.bf = 1
cur.bf = cur_right.bf = 0
else:
cur.bf = -1
cur_right.bf = par.bf = 0
右左双旋转
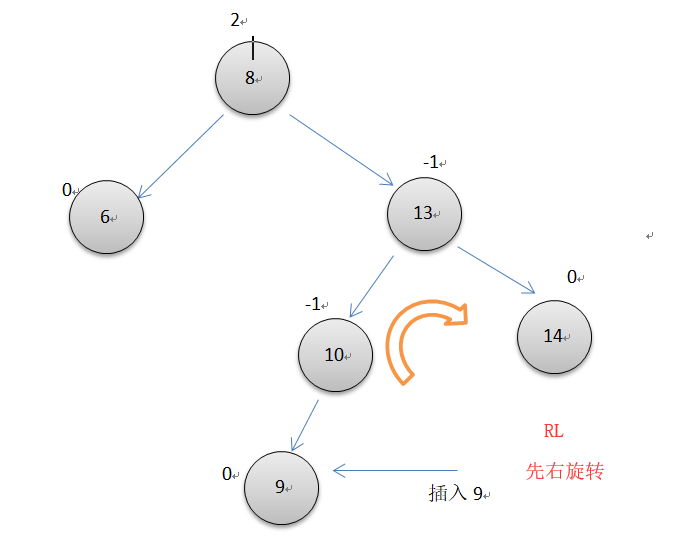
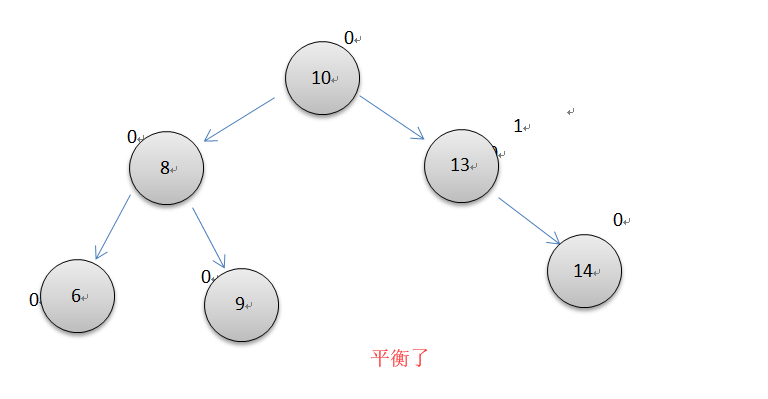
如上图所示，当一个节点的平衡因子为2，而它的右子节点的平衡因子为-1时，就需要先进行右旋转，再左旋转。注意中间节点13右旋转后的平衡因子变为1了。代码同左右双旋转类似。
def rl_rotate(self, par, cur):
"""右左双旋转"""
# 先右旋转 cur 和 cur的左子节点
cur_left = cur.left # 获得cur的右子节点的引用
bf = cur_left.bf
self.r_rotate(cur, cur_left)
self.l_rotate(par, cur_left) # 继续右旋转
if bf == 0: # 根据cur_left的平衡因子更新操作的3个节点
cur.bf = cur_left.bf = par.bf = 0
elif bf == -1:
cur.bf = 1
par.bf = cur_left.bf = 0
else:
par.bf = -1
cur_left.bf = cur.bf = 0
平衡因子的更新
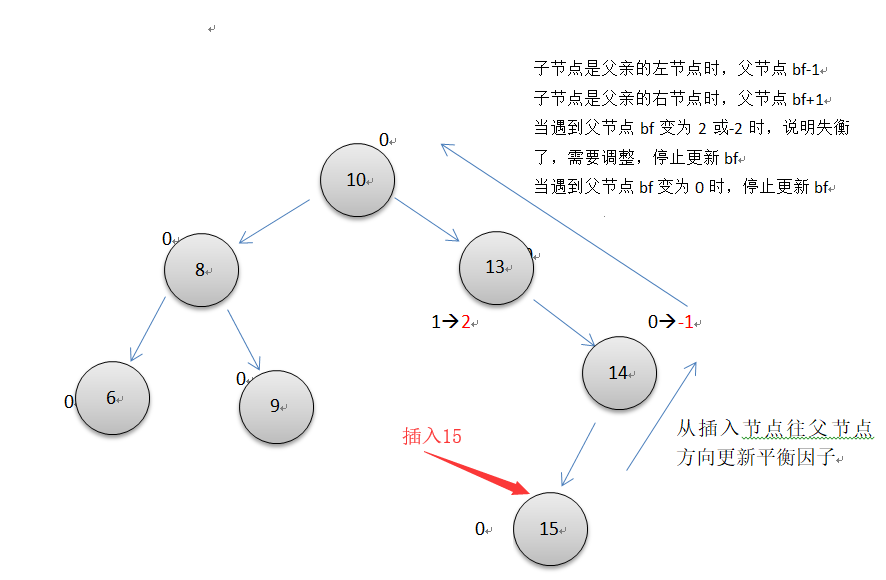
平衡因子的代码如下所示
def balance_by_insert(self, cur):
"""
更新插入后的平衡因子, 平衡二叉树
:param cur: 当前插入节点cur
:return: None
"""
par = cur.parent # 插入节点的父节点
while par:
if cur == par.left: # 如果当前节点是父节点的左节点
par.bf -= 1
else:
par.bf += 1
if par.bf == 0: # 为0说明没有增加树的高度, 返回
return
if par.bf == -2:
if cur.bf == 1: # 左右双向旋转
self.lr_rotate(par, cur)
break
else:
self.r_rotate(par, cur)
break
elif par.bf == 2:
if cur.bf == -1: # 右左双向旋转
self.rl_rotate(par, cur)
break
else:
self.l_rotate(par, cur)
break
cur = par # 从添加的节点开始往上更新直到根节点
par = par.parent
查找
比起插入操作来说，查找就容易多了，从根节点开始遍历...代码如下
def find(self, key):
"""寻找键值"""
p = self.root
while p:
if p.key == key:
return p
if key < p.key:
p = p.left
else:
p = p.right
return None
删除细节
删除操作也是一个难点，要考虑几种不同的情况
第一种情况
当要删除的节点直接是叶节点，那就直接删除
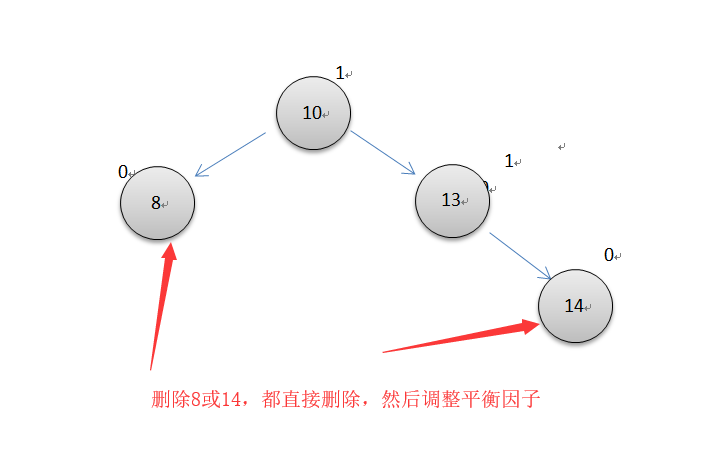
第二种情况
要删除的节点带有左子串或右子串
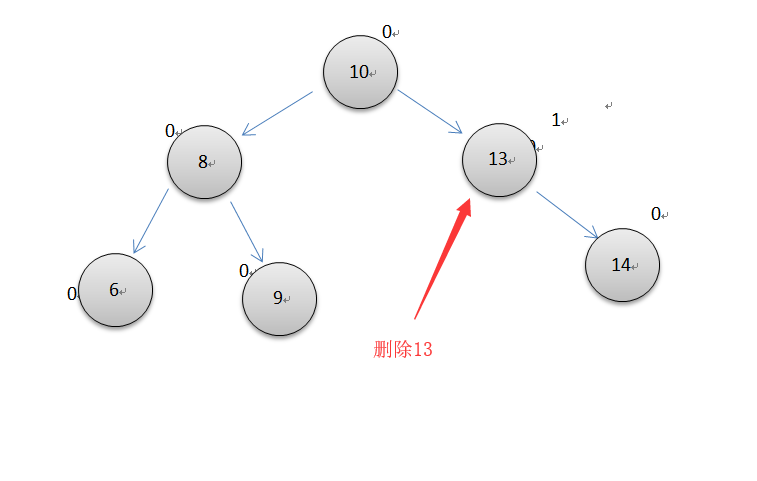
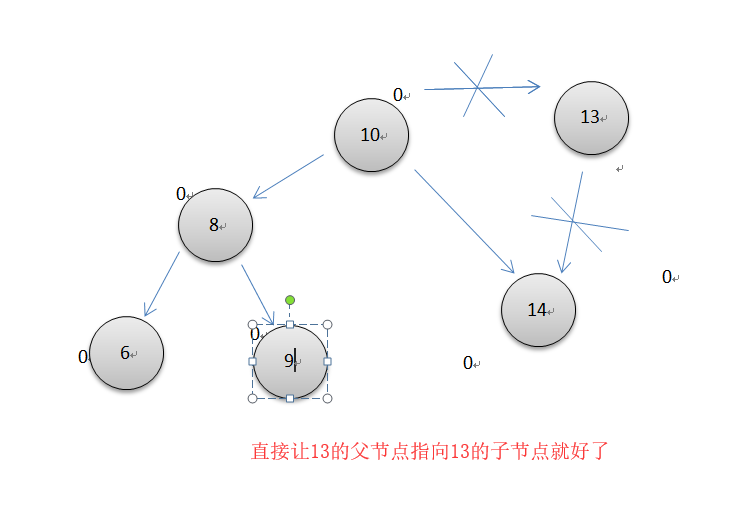
第三种情况
要删除的节点带有左子串和右子串
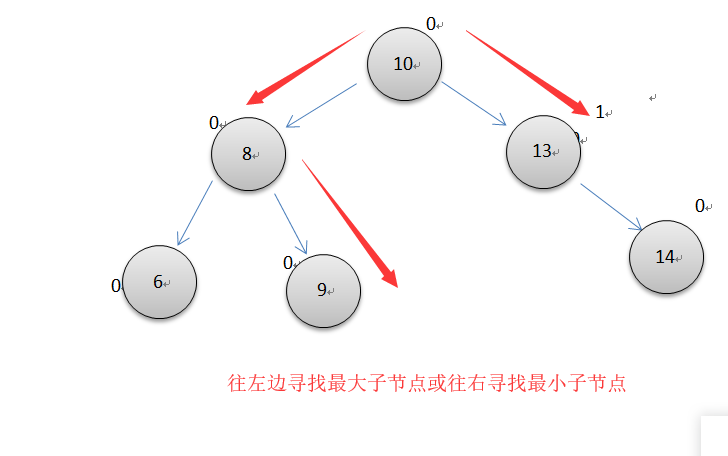
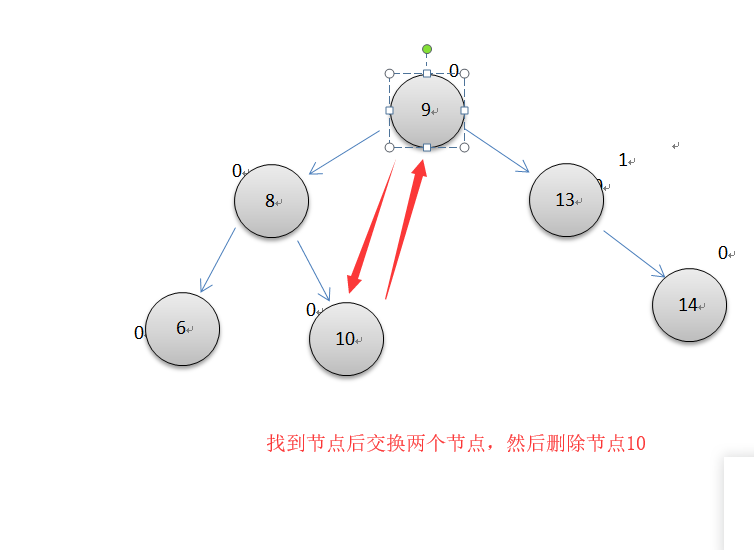
遇到第三种情况，就往左寻找最大子节点，或往右寻找最小子节点。找到交换完元素后，如上图所示，原来的节点9是叶节点，这就转换为情况一了，然后直接删除节点10，如果交换的节点原本就有子串，如上图，假设9有左子串，那么就相当于把情况转换为情况2了，变为删除一个带子节点的节点了。
删除的平衡因子更新
删除操作中，平衡因子的更新和插入操作类似，都是从删除节点的位置开始向父节点方向开始更新，更新时如果子节点是父节点的左节点，则父节点的bf+1，否则-1。直到根节点或原本平衡因子0的父节点因删除而变为1或为-1时才停下来。此时还要注意有一个关键与插入不同，当遇到一个节点不平衡时，旋转后可能还要继续往父节点处更新bf，只有两种特殊情况旋转后因为子节点高度没变，就不用往上更新了，下面有说明。
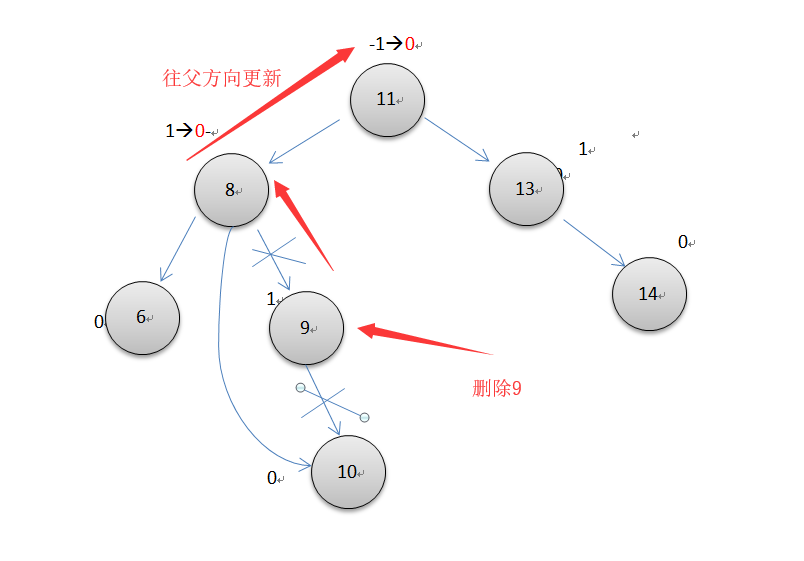
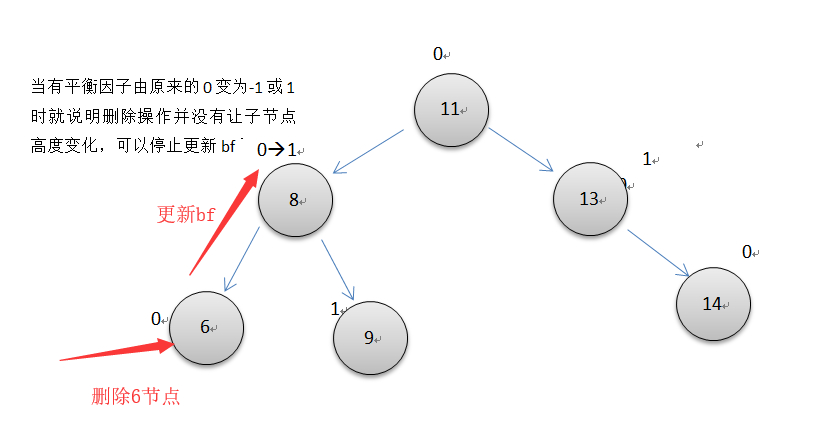
删除操作遇到不平衡的节点时也可以通过旋转恢复平衡，但旋转后可能需要继续往父节点更新平衡因子
当遇到下面两种情况时，参与左单旋转或右单旋转的两个节点的平衡因子并没有如插入操作一样恢复为0，但是因为这两种情况旋转后树的高度没变，所以可以停止往上更新平衡因子了。
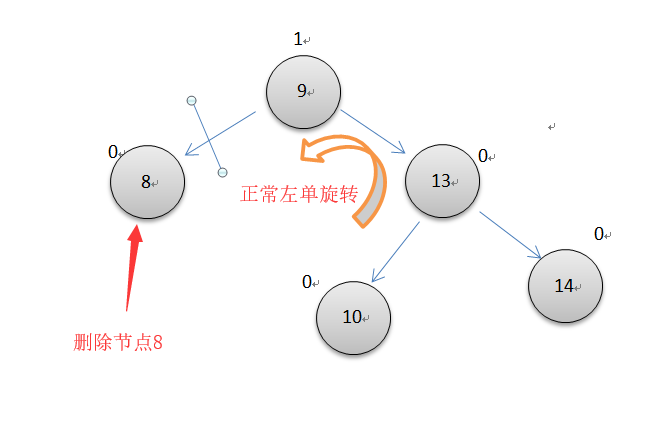
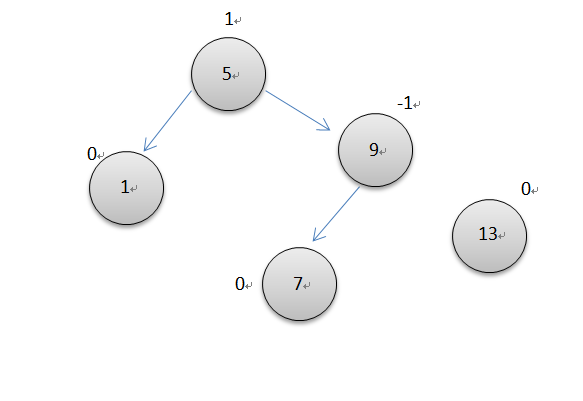
遇到上面两种情况单独处理就是了。以下是删除后的更新平衡因子的代码
def balance_by_delete(self, cur):
"""根据删除节点位置向上更新平衡因子"""
par = cur.parent
while par:
if cur == par.left: # 如果当前节点是父节点的左节点
par.bf += 1
else:
par.bf -= 1
if par.bf == 1 or par.bf == -1: # 为0说明没有增加树的高度, 返回
return
if par.bf == -2:
cur = cur.parent.left # 旋转是旋转与插入方向相反的两个节点
if cur.bf == 1: # 左右双向旋转
self.lr_rotate(par, cur)
par = cur.parent # 更新一下par的指向
elif cur.bf == 0:
self.r_rotate(par, cur) # 特殊情况树的高度并没有增加需要退出往上更新
cur.bf = 1
par.bf = -1
break
else:
self.r_rotate(par, cur)
par = cur
elif par.bf == 2:
cur = cur.parent.right
if cur.bf == -1: # 左右双向旋转
self.rl_rotate(par, cur)
par = cur.parent # 更新一下par的指向
elif cur.bf == 0:
self.l_rotate(par, cur)
cur.bf = -1
par.bf = 1
break
else:
self.l_rotate(par, cur)
par = cur
cur = par # 从添加的节点开始往上更新直到根节点
par = par.parent
二叉树的图形化显示
1. 在线生成bst树和avl树
学习过程中难免遇到理解的问题: 图形化能很好的帮助我们理解问题，下面是两个在线生成二叉树的网址，根据自己需要看看，添加添加
2. 程序自己生成二叉树
利用PyGraphviz模块画出二叉树
参考网址：http://pygraphviz.github.io/documentation/pygraphviz-1.5/ 这里有详细的使用说明
安装该模块失败，参考这篇博客 https://blog.csdn.net/chirebingxue/article/details/50393755
我这次使用了该模块以完成最后生成的二叉树显示，代码如下
import pygraphviz as pgv
def draw(self, filename='./tree.png'):
g = pgv.AGraph(strict=False, directed=True)
g.node_attr['shape'] = 'circle' def traver(node):
if node:
if not node.parent:
g.add_node(node.key)
else:
g.add_edge(node.parent.key, node.key)
traver(node.left)
traver(node.right)
traver(self.root)
g.layout('dot')
g.draw(filename)
简单的测试改模块的效果
tree = AVLTree()
tree.insert(range(0, 20, 2)) # 自己简单实现了个可以接受一个可迭代对象的数值的插入
tree.draw()
tree.delete_key(14)
tree.draw('tree2.png')
最后生成下面的png图
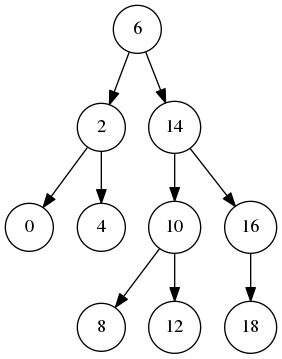
完整代码
最后附上个人的完整代码
"""实现一个自平衡的AVLtree"""
from collections import deque, Iterable
import pygraphviz as pgv
import random class Node(object):
def __init__(self, key, parent=None, left=None, right=None):
self.key = key # 存储的数据
self.parent = parent # 父节点
self.left = left # 左孩子节点
self.right = right # 右孩子节点
self.bf = 0 # 平衡因子 等于左子树高度减去右子树高度 class AVLTree(object):
def __init__(self, key=None):
if key:
self.root = Node(key)
else:
self.root = None def insert(self, *keys):
"""插入键值，键可以是个可迭代对象，或是多个独立的键"""
if isinstance(keys[0], Iterable):
if len(keys) > 1:
print("插入失败...第一个参数可迭代对象时参数只能有一个")
return
keys = keys[0]
else:
keys = keys
for key in keys:
if not self.root:
self.root = Node(key)
else:
p = self.root
while 1:
if key == p.key:
print("%d键已存在, 跳过该键" % key)
break
elif key < p.key:
if not p.left: # 当前左节点可以添加
cur_node = Node(key, p)
p.left = cur_node
self.balance_by_insert(cur_node)
break
else:
p = p.left
else:
if not p.right:
cur_node = Node(key, p)
p.right = cur_node
self.balance_by_insert(cur_node)
break
else:
p = p.right def balance_by_insert(self, cur):
"""
更新插入后的平衡因子, 平衡二叉树
:param cur: 当前插入节点cur
:return: None
"""
par = cur.parent # 插入节点的父节点
while par:
if cur == par.left: # 如果当前节点是父节点的左节点
par.bf -= 1
else:
par.bf += 1
if par.bf == 0: # 为0说明没有增加树的高度, 返回
return
if par.bf == -2:
if cur.bf == 1: # 左右双向旋转
self.lr_rotate(par, cur)
break
else:
self.r_rotate(par, cur)
break
elif par.bf == 2:
if cur.bf == -1: # 左右双向旋转
self.rl_rotate(par, cur)
break
else:
self.l_rotate(par, cur)
break
cur = par # 从添加的节点开始往上更新直到根节点
par = par.parent def balance_by_delete(self, cur):
"""根据删除节点位置向上更新平衡因子"""
par = cur.parent
while par:
if cur == par.left: # 如果当前节点是父节点的左节点
par.bf += 1
else:
par.bf -= 1
if par.bf == 1 or par.bf == -1: # 为0说明没有增加树的高度, 返回
return
if par.bf == -2:
cur = cur.parent.left # 旋转是旋转与插入方向相反的两个节点
if cur.bf == 1: # 左右双向旋转
self.lr_rotate(par, cur)
par = cur.parent # 更新一下par的指向
elif cur.bf == 0:
self.r_rotate(par, cur) # 特殊情况树的高度并没有增加需要退出往上更新
cur.bf = 1
par.bf = -1
break
else:
self.r_rotate(par, cur)
par = cur
elif par.bf == 2:
cur = cur.parent.right
if cur.bf == -1: # 左右双向旋转
self.rl_rotate(par, cur)
par = cur.parent # 更新一下par的指向
elif cur.bf == 0:
self.l_rotate(par, cur)
cur.bf = -1
par.bf = 1
break
else:
self.l_rotate(par, cur)
par = cur
cur = par # 从添加的节点开始往上更新直到根节点
par = par.parent def delete_key(self, key):
"""删除键值, 通过三个子函数实现功能处理三种情况""" def first(node):
"""第一种情况, 找到的键本身是叶节点, 直接删除"""
self.balance_by_delete(node)
if node == node.parent.left:
node.parent.left = None
else:
node.parent.right = None
del node def second(node):
"""第二种, 找到的键本身带有左子节点或右子节点"""
par = node.parent # 获得该键的父节点引用
if node.left: # 该节点只有左节点
if par is None: # 说明该节点是root
self.root = node.left
node.left.parent = None
elif node == par.left: # 该节点是父节点的左节点
par.left = node.left
node.left.parent = par
else:
par.right = node.left
node.left.parent = par
self.balance_by_delete(node.left)
else:
if par is None:
self.root = node.right
node.left.parent = None
elif node == par.left:
par.left = node.right
node.right.parent = par
else:
par.right = node.right
node.right.parent = par
self.balance_by_delete(node.right)
del node def third(node):
p = node.left # 寻找左边最大的子节点代替
while p.right:
p = p.right # 寻找最大子节点 node.key, p.key = p.key, node.key # 交换两个节点，这里的交换取了个巧，只交换值就不用处理节点之间的复杂关系了
if p.left or p.right: # 转换为第二种或第一种情况
second(p)
else:
first(p) cur = self.find(key) # 寻找要删除的值
if cur:
if cur.left and cur.right:
third(cur)
elif not cur.left and not cur.right: # 直接是叶节点, 第一种情况
first(cur)
else: # 第二种情况, 只有左节点或右节点
second(cur)
else:
print("键值不存在, 删除失败") def find(self, key):
"""寻找键值"""
p = self.root
while p:
if p.key == key:
return p
if key < p.key:
p = p.left
else:
p = p.right
return None def r_rotate(self, par, cur):
"""右单旋转"""
p = cur.right
cur.right = par
par.left = p
if p:
p.parent = par
if par == self.root:
self.root = cur
else:
if par == par.parent.left:
par.parent.left = cur
else:
par.parent.right = cur cur.parent = par.parent # 更新父节点信息
par.parent = cur
cur.bf = par.bf = 0 # 更新平衡因子 def l_rotate(self, par, cur):
"""
左单旋转
:param par: 平衡因子为2|-2的节点
:param cur: 作为轴心旋转的节点(平衡因子不为2)
:return: None
"""
p = cur.left # 辅助引用p指向cur的左节点
cur.left = par # cur的左节点指向par
par.right = p # par的右节点指向cur的左节点
if p:
p.parent = par # cur的左节点不为空时更新该节点的父节点
if par == self.root:
self.root = cur # 判断平衡因子为2的par是否为根
else:
if par == par.parent.left: # 更新par父节点的子节点信息
par.parent.left = cur
else:
par.parent.right = cur
cur.parent = par.parent # 当前cur的父节点指向原来par的父节点
par.parent = cur # par变为cur的左子节点 cur.bf = par.bf = 0 # 插入操作中, 操作的两个节点旋转后平衡因子恢复为0 def lr_rotate(self, par, cur):
"""左右双旋转"""
# 先左旋转 cur 和 cur的右子节点
cur_right = cur.right # 获得cur的右子节点的引用
bf = cur_right.bf
self.l_rotate(cur, cur_right)
# 继续右旋转
self.r_rotate(par, cur_right)
if bf == 0: # 根据cur_right的平衡因子更新操作的3个节点
cur.bf = cur_right.bf = par.bf = 0
elif bf == -1:
par.bf = 1
cur.bf = cur_right.bf = 0
else:
cur.bf = -1
cur_right.bf = par.bf = 0 def rl_rotate(self, par, cur):
"""右左双旋转"""
# 先右旋转 cur 和 cur的左子节点
cur_left = cur.left # 获得cur的右子节点的引用
bf = cur_left.bf
self.r_rotate(cur, cur_left)
self.l_rotate(par, cur_left) # 继续右旋转
if bf == 0: # 根据cur_left的平衡因子更新操作的3个节点
cur.bf = cur_left.bf = par.bf = 0
elif bf == -1:
cur.bf = 1
par.bf = cur_left.bf = 0
else:
par.bf = -1
cur_left.bf = cur.bf = 0 def get_tree_state(self, _tree=None):
"""返回树的高度和元素数量和树是否平衡组成的一个元祖"""
if not _tree:
_tree = self.root
count = 0
is_balanced = True def get_state(_tree):
nonlocal count, is_balanced
if not _tree:
return 0
count += 1
h1 = get_state(_tree.left) + 1
h2 = get_state(_tree.right) + 1
if abs(h1 - h2) >= 2:
is_balanced = False
return max((h1, h2))
return get_state(_tree), count, is_balanced def pre_traversal(self):
"""先序遍历"""
def traver(node):
if node:
print(node.key, end=' ')
traver(node.left)
traver(node.right) traver(self.root)
print() def in_order_traversal(self):
"""中序遍历"""
_node = self.root def traver(node):
if node:
traver(node.left)
print(node.key, end=' ')
traver(node.right) traver(_node)
print() def level_traversal(self):
"""层次遍历, 自己简单把树分层打印出来"""
d = deque()
d.append((1, 1, self.root)) # 元祖表示第1层第1个数
level = 2
level_count = 0 # 每层的数量
last_l = 1
while d:
# p = d.popleft()
ll, c, p = d.popleft()
if ll != last_l:
last_l = ll
print("")
# print(p.key, 'bf: %s' % p.bf, end=' ')
print(p.key, end=' ')
level_count += 1
if p.left:
d.append((level, level_count, p.left)) level_count += 1
if p.right:
d.append((level, level_count, p.right))
if level_count == pow(2, level-1):
level_count = 0
level += 1
print() def draw(self, filename='./tree.png'):
"""生成二叉树的图片文件"""
g = pgv.AGraph(strict=False, directed=True)
g.node_attr['shape'] = 'circle' def traver(node):
if node:
if not node.parent:
g.add_node(node.key)
else:
g.add_edge(node.parent.key, node.key)
traver(node.left)
traver(node.right)
traver(self.root)
g.layout('dot')
g.draw(filename)
AVLTree
测试代码:
from AVL_Tree import AVLTree
import random
import os path = './tree_pic'
if not os.path.exists(path):
os.mkdir(path) # 创建一个生成器, 做图片的名称
g = (path + '/tree' + str(i) + '.png' for i in range(1, 30)) t = AVLTree()
# lst = [random.randrange(20, 300) for i in range(20)]
lst = random.sample(range(30, 300), 20)
t.insert(lst)
print(lst)
t.draw(next(g))
print(t.get_tree_state())
for i in range(8):
k = random.choice(lst)
print("删除键%d" % k)
t.delete_key(k)
print(t.get_tree_state()) # 打印树的高度, 元素个数，树是否平衡
t.draw(next(g)) t.insert(-5, 200, 300)
t.insert(10, 0, 410, 15, 500)
t.draw(next(g))
print(t.get_tree_state())
控制台输出
[100, 89, 217, 202, 206, 98, 187, 34, 293, 162, 292, 236, 279, 37, 269, 80, 237, 52, 222, 155]
(5, 20, True)
删除键217
(5, 19, True)
删除键155
(5, 18, True)
删除键217
键值不存在, 删除失败
(5, 18, True)
删除键293
(5, 17, True)
删除键98
(5, 16, True)
删除键98
键值不存在, 删除失败
(5, 16, True)
删除键52
(5, 15, True)
删除键292
(5, 14, True)
(6, 22, True)
生成的二叉树的前两张和最后一张图片
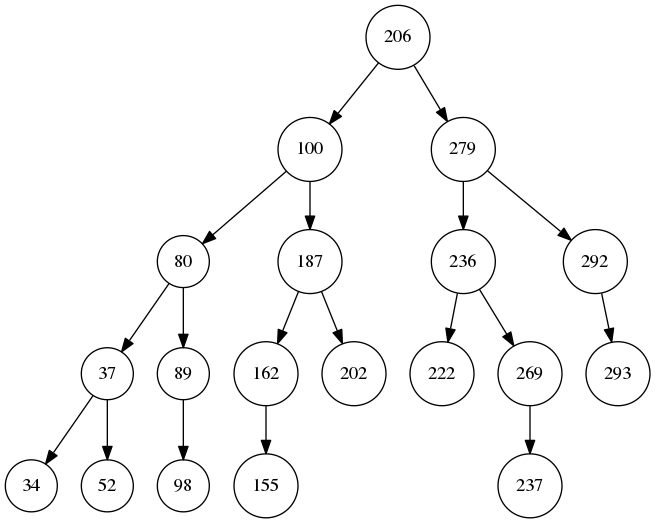
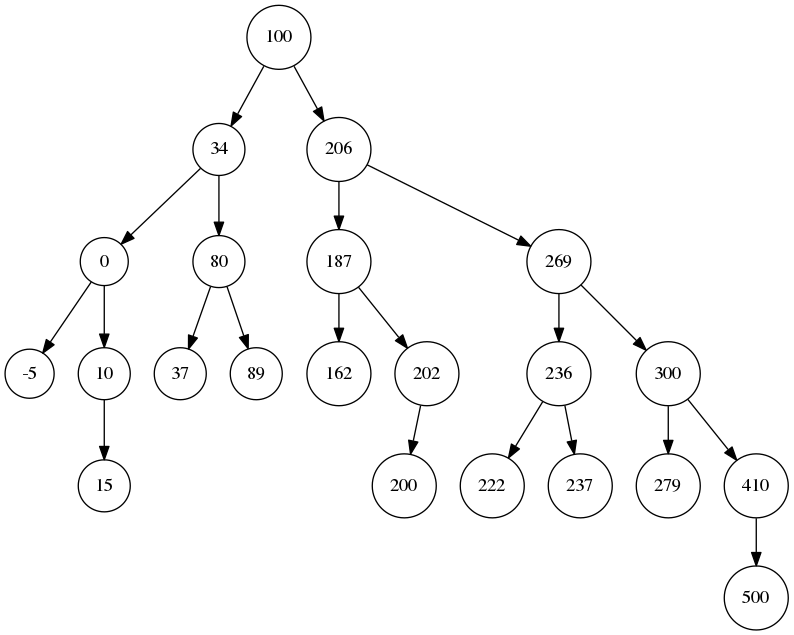
参考:
感谢他们的博客
- https://blog.csdn.net/qq_37941471/article/details/79706523
- https://www.cnblogs.com/fullsail/p/3729015.html?utm_source=tuicool
- http://www.cnblogs.com/skywang12345/p/3577479.html
AVLTree的Python实现的更多相关文章
- 详细理解平衡二叉树AVL与Python实现
前言 上一篇文章讨论的二叉搜索树,其时间复杂度最好的情况下是O(log(n)),但是最坏的情况是O(n),什么时候是O(n)呢? 像这样: 如果先插入10,再插入20,再插入30,再插入40就会成上边 ...
- AVL树Python实现(使用递推实现添加与删除)
# coding=utf-8 # AVL树的Python实现(树的节点中包含了指向父节点的指针) def get_height(node): return node.height if node el ...
- AVL树Python实现
# coding=utf-8 # AVL树Python实现 def get_height(node): return node.height if node else -1 def tree_mini ...
- Python与数据结构[3] -> 树/Tree[2] -> AVL 平衡树和树旋转的 Python 实现
AVL 平衡树和树旋转 目录 AVL平衡二叉树 树旋转 代码实现 1 AVL平衡二叉树 AVL(Adelson-Velskii & Landis)树是一种带有平衡条件的二叉树,一棵AVL树其实 ...
- Python实现AVL树
参考: https://www.cnblogs.com/linxiyue/p/3659448.html?utm_source=tuicool&utm_medium=referral class ...
- Python中的多进程与多线程（一）
一.背景 最近在Azkaban的测试工作中,需要在测试环境下模拟线上的调度场景进行稳定性测试.故而重操python旧业,通过python编写脚本来构造类似线上的调度场景.在脚本编写过程中,碰到这样一个 ...
- Python高手之路【六】python基础之字符串格式化
Python的字符串格式化有两种方式: 百分号方式.format方式 百分号的方式相对来说比较老,而format方式则是比较先进的方式,企图替换古老的方式,目前两者并存.[PEP-3101] This ...
- Python 小而美的函数
python提供了一些有趣且实用的函数,如any all zip,这些函数能够大幅简化我们得代码,可以更优雅的处理可迭代的对象,同时使用的时候也得注意一些情况 any any(iterable) ...
- JavaScript之父Brendan Eich，Clojure 创建者Rich Hickey，Python创建者Van Rossum等编程大牛对程序员的职业建议
软件开发是现时很火的职业.据美国劳动局发布的一项统计数据显示,从2014年至2024年,美国就业市场对开发人员的需求量将增长17%,而这个增长率比起所有职业的平均需求量高出了7%.很多人年轻人会选择编 ...
随机推荐
- MAVEN（一） 安装和环境变量配置
一.安装步骤 1.安装maven之前先安装jdk,并配置好环境变量.确保已安装JDK,并 “JAVA_HOME” 变量已加入到 Windows 环境变量. 2.下载maven 进入官方网站下载网址如下 ...
- 关于php注释那些事
代码注释的作用 --- 为自己,也为别人. 永远不要过于相信自己的理解力!当你思路通畅,思如泉涌,进入编程境界,你可以很流畅的实现某个功能,但这种一泻千里的流畅可能只停留在了当时的状态.当你几个月, ...
- 使用jieba分析小说人物出现次数
分析: 1. 读取小说,以读的形式打开 with open('文件名.txt','r',encoding='utf8') as f: str = f.read() 2. 切割小说 ret = jieb ...
- mine：dp
一个小的线性dp.方法很多,八仙过海各显神通. 我想讲一下我的: #include<cstdio> #define mod 1000000007 ];][][],n;//是不是雷,右边有没 ...
- javaScript中this到底指向谁
1.前言 在JavaScript中,this的指向一直是大多数初学者的易错点,总是搞不清楚this到底指向谁,而在求职面试中,this的指向问题往往又是高频考点.本篇博文就来总结一下在JavaScri ...
- 苹果审核ipv6海外解决思路-About APP Store
原始简书文章地址(也是我自己的) 首先声明,一我不负责涉及你们内部服务器. 二是好好读文章,别人能过,你们也能过 苹果6月1日出的IPV6协议阻碍了国内大多数积极开发者,我司也不外乎,经过三次被拒后, ...
- mjpg-stream 视频服务 （1）| 简介与配置树莓派使用
源码地址为:https://github.com/jacksonliam/mjpg-streamer Mjpg简介: (1)mjpg-streamer是一个命令行应用程序,它将JPEG帧从一个或多个输 ...
- java中 equals和==区别
一.java当中的数据类型和“==”的含义: 基本数据类型(也称原始数据类型) :byte,short,char,int,long,float,double,boolean.他们之间的比较,应用双等号 ...
- MBR分区表的备份与还原
MBR分区表的备份与还原 MBR分区的存储 从下图可以看出,MBR分区前446字节是boot loader:接下来64字节是分区表:再然后就是三个主分区加一个拓展分区. 一.备份分区表,要跳过前446 ...
- ChickenLegend Image