yzoj P2045 不老的传说 题解

题意

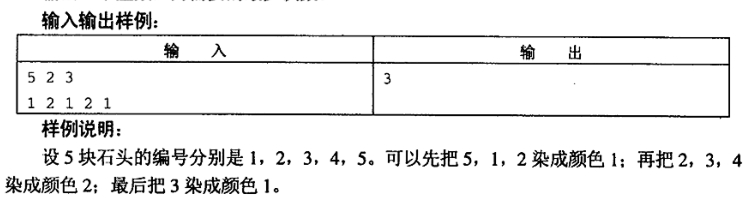
类似于涂色问题，环形问题不多说，断环加倍即可，限制条件if判断就行。

解析

代码

#include<bits/stdc++.h>
using namespace std;
int n,c,p,a[410];
int f[410][410],ans=1<<30;
int main(){
	scanf("%d %d %d",&n,&c,&p);
	for(int i=1;i<=n;++i){
		scanf("%d",&a[i]);
		a[i+n]=a[i];
	}
	memset(f,0x3f,sizeof(f));
	for(int i=1;i<=n;++i){
		f[i][i]=f[i+n][i+n]=1;
	}
	for(int l=2;l<=n;++l){
		for(int i=1;i<=2*n-l+1;++i){
			int j=i+l-1;
			if(a[i]==a[j]&&l<=p) f[i][j]=min(f[i+1][j],f[i][j-1]);
			else {
				for(int k=i;k<j;++k){
					f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]);
				}
			}
		}
	}
	for(int i=1;i<=n;++i){
		if(f[i][i+n-1]){
			ans=min(ans,f[i][i+n-1]);
		}
	}
	printf("%d",ans);
	return 0;
}
/*
5 2 3
1 2 1 2 1
*/