MIT线性代数:7.主变量,特解,求解AX=0
MIT线性代数:7.主变量,特解,求解AX=0的更多相关文章
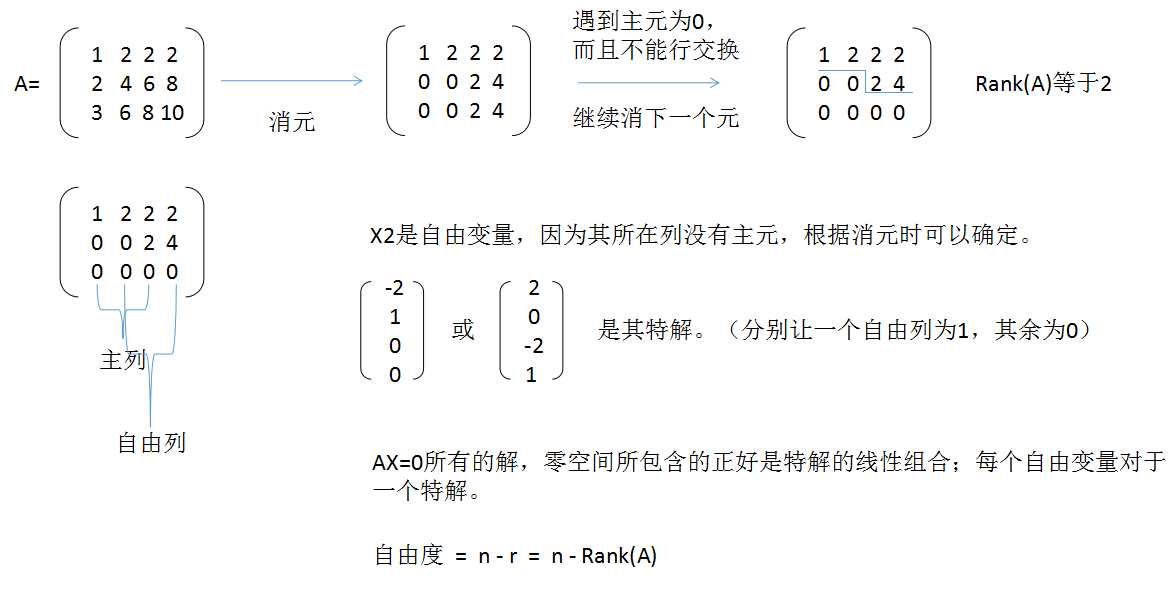
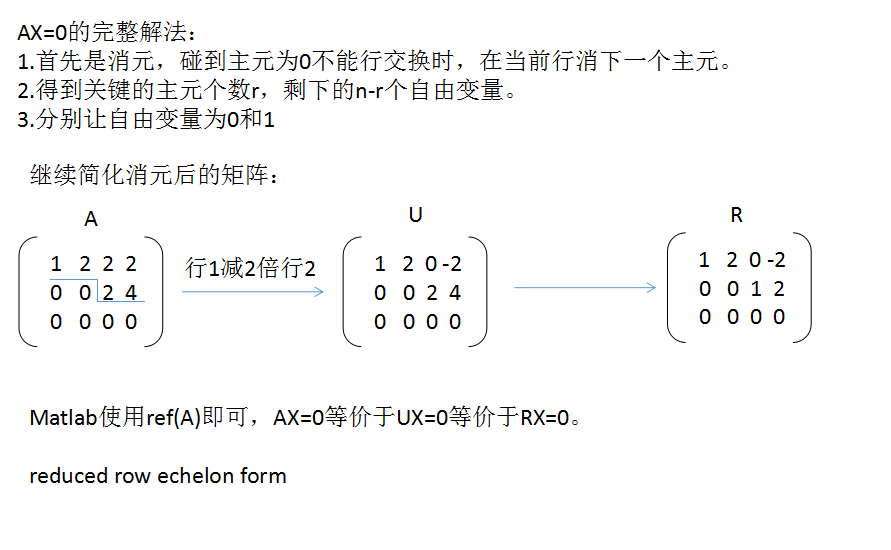
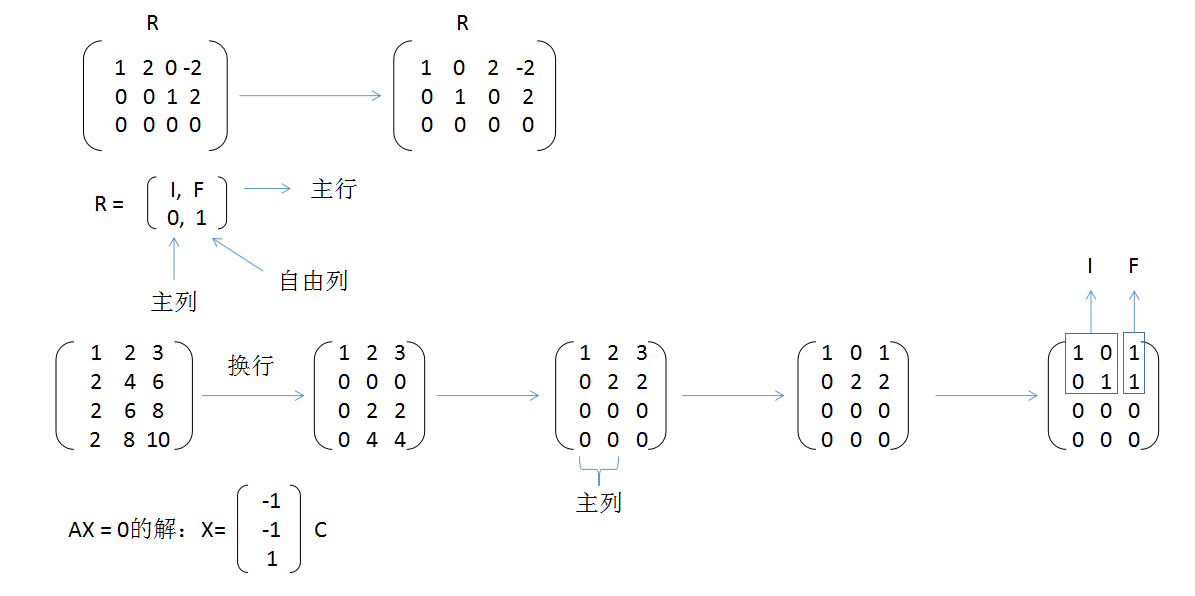
- 07-求解Ax=0:主变量、特解
一.定义转向算法 在第六节讲了空间,列空间,零空间的定义,这节主要讲解如何求出这些空间,即求解$Ax=0$的过程是怎么样的过程,以下面的矩阵$A$为例:(这里主要是长方阵) $A=\left[\beg ...
- 求解Ax=b
一 线性方程组 Ax=b 的解释 线性方程组 Ax=b,其中矩阵 A 尺寸为 m*n, 当 A 为方正时,可使用消元法判断解是否存在并求解.当 A 为长方形矩阵时,同样可使用消元法判断解存在情况并求解 ...
- MIT线性代数课程 总结与理解-第一部分
概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...
- phpinfo() 中 Local Value(局部变量)Master Value(主变量) 的区别
[题外话]phpinfo()这个函数可以查看很多php的信息,要 记得使用 phpinfo() 的很多部分有两个Column:Local Value(局部变量)和 Master Value(主变量) ...
- 【读书笔记】:MIT线性代数(5):Four fundamental subspaces
At the beginning, the difference between rank and dimension: rank is a property for matrix, while di ...
- 【读书笔记】:MIT线性代数(3):Special Solution, Rank and RREF
Special Solutions: Notice what is special about s 1 and S2. They have ones and zeros in the last two ...
- 【读书笔记】:MIT线性代数(2):Vector Spaces and Subspaces
Vector Space: R1, R2, R3,R4 , .... Each space Rn consists of a whole collection of vectors. R5 conta ...
- 错误: 找不到或无法加载主类 Files\apache-activemq-5.10.0\bin\..\conf\login.config
在启动activemq的时候出现错误:“错误: 找不到或无法加载主类 Files\apache-activemq-5.10.0\bin\..\conf\login.config”,之前用activem ...
- javascript中判断变量时变量值为 0 的特殊情况
有时候我们在js中会直接判断变量是否存在值,下面列举一些情况: var a = 0; var b = 1; var c = ' '; var d; console.log( a ? 1 : null) ...
随机推荐
- redis常用笔记(第一版)
1.SINTER 说明:多key之间取交集数据 key1 = {a,b,c,d} key2 = {c} key3 = {a,c,e} SINTER key1 key2 key3 = {c} 2.sad ...
- MapReduce与Yarn 的详细工作流程分析
MapReduce详细工作流程之Map阶段 如上图所示 首先有一个200M的待处理文件 切片:在客户端提交之前,根据参数配置,进行任务规划,将文件按128M每块进行切片 提交:提交可以提交到本地工作环 ...
- Spark 学习笔记之 Spark history Server 搭建
在hdfs上建立文件夹/directory hadoop fs -mkdir /directory 进入conf目录 spark-env.sh 增加以下配置 export SPARK_HISTORY ...
- 高清屏下canvas重置尺寸引发的问题
我们知道,清空canvas画布内容有以下两个方法. 第一种方法是cearRect函数: context.cearRect(0,0,canvas.width,canvas.height) 第二种方法就是 ...
- 【NOIP模拟赛】小奇挖矿 2
[题目背景] 小奇飞船的钻头开启了无限耐久+精准采集模式!这次它要将原矿运到泛光之源的矿石交易市场,以便为飞船升级无限非概率引擎. [问题描述] 现在有m+1个星球,从左到右标号为0到m,小奇最初在0 ...
- [ERROR ImagePull]: failed to pull image [k8s.gcr.io/kube-apiserver-amd64:v1.11.1]: exit status 1
问题描述 [root@localhost ~]# kubeadm init --kubernetes-version=v1.11.1 --pod-network-cidr=10.244.0.0/16 ...
- PHP绕过disable_function限制(一)
测试环境 php 5.4.5 0x01 利用系统组件绕过 1.window com组件(php 5.4)(高版本扩展要自己添加) (COM组件它最早的设计意图是,跨语言实现程序组件的复用.) 测试: ...
- XSS中的同源策略和跨域问题
转自 https://www.cnblogs.com/chaoyuehedy/p/5556557.html 1 同源策略 所谓同源策略,指的是浏览器对不同源的脚本或者文本的访问方式进行的限制.比如源a ...
- pdfminer API介绍:pdf网页爬虫
安装 pip install pdfminer 爬取数据是数据分析项目的第一个阶段,有的加密成pdf格式的文件,下载后需要解析,使用pdfminer工具. 先介绍一下什么是pdfminer 下面是官方 ...
- .Net Core3.0 配置Configuration
准备 .NET core和.NET项目配置上有了很大的改变,支持的也更加丰富了比如命令行,环境变量,内存中.NET对象,设置文件等等..NET项目我们常常把配置信息放到webConfig 或者appC ...
