Cesium原理篇：3最长的一帧之地形(4：重采样)

地形部分的原理介绍的差不多了，但之前还有一个刻意忽略的地方，就是地形的重采样。通俗的讲，如果当前Tile没有地形数据的话，则会从他父类的地形数据中取它所对应的四分之一的地形数据。打个比方，当我们快速缩放影像的时候，下一级的影像还没来得及更新，所以会暂时把当前Level的影像数据放大显示，一旦对应的影像数据下载到当前客户端后再更新成精细的数据。Cesium中对地形也采用了这样的思路。下面我们具体介绍其中的详细内容。

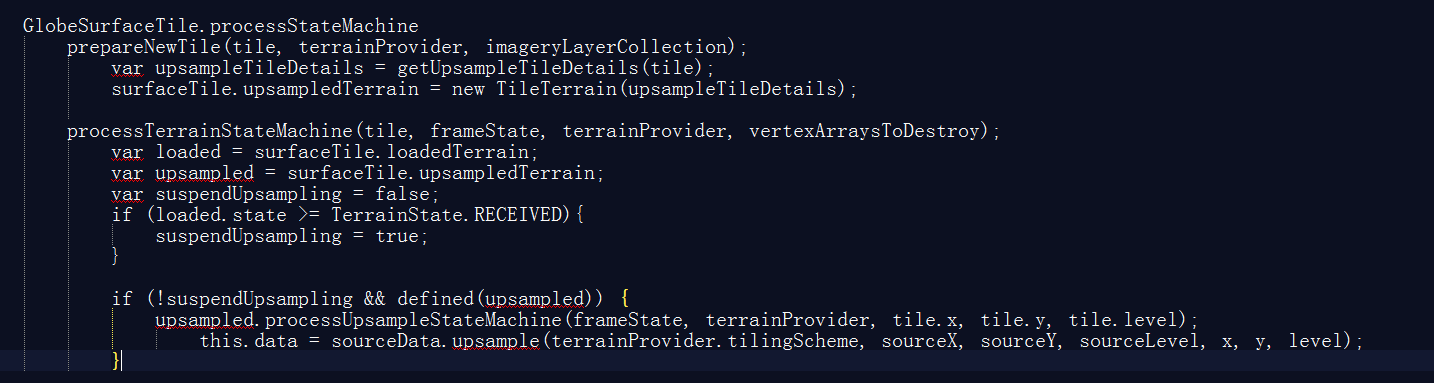
上图是一个大概流程，在创建Tile的时候（prepareNewTile），第一时间会获取该Tile父节点的地形数据（upsampleTileDetails），然后构造出upsampledTerrain对象，它是TileTerrain对象，只是一个包含父类地形信息的空壳。接着，开始创建地形网格（processTerrainStateMachine）。

这里就有两个逻辑，如果当前没有地形数据，也就是EllipsoidTerrainProvider的情况，这样会直接创建HeightmapTerrainData。因此状态是TerrainState.RECEIVED，这种情况下不需要重采样；如果请求了真实的地形数据，比如CesiumTerrainProvider，无论是请求高度图还是STK，只要有异步请求，则会执行processUpsampleStateMachine韩式，最终实现重采样（sourceData.upsample）。

HeightmapTerrainData.prototype.upsample

我们先了解一下高度图下的实现。高度图，顾名思义也是一种图了，所以这个重采样的方式和普通的图片拉伸算法一致。比如一个2*2的图片，放大至4*4的大小，这里就有一个插值的过程。比如线性差值，会取相邻的两个像素颜色，加权求值，或者双线性插值，取周边四个像素，加权求值。这让我想到了GDI中对图片是采用线性了，而Photoshop里面则有很多专业的选项，某些逗逼用户经常拿着PS拉伸的效果来做对比，说我们图片拉伸的效果不如PS。等我们做完了，又拿CorelDraw来对比矢量效果。但你有很难从技术和产品的角度来和用户沟通其中的利弊。这是题外话了，我们来看一下Cesium具体的代码：

for (var j = 0; j < height; ++j) {

    var latitude = CesiumMath.lerp(destinationRectangle.north, destinationRectangle.south, j / (height - 1));

    for (var i = 0; i < width; ++i) {

        var longitude = CesiumMath.lerp(destinationRectangle.west, destinationRectangle.east, i / (width - 1));

        var heightSample = interpolateMeshHeight(buffer, encoding, heightOffset, heightScale, skirtHeight, sourceRectangle, width, height, longitude, latitude, exaggeration);

        setHeight(heights, elementsPerHeight, elementMultiplier, divisor, stride, isBigEndian, j * width + i, heightSample);

    }

}

这是两个for循环，遍历目标图片中每一个经纬度对应父类图片中该位置的高度值。下面是一个切片四叉树的示意图，高度图也是一个思路，只是其中每一个像素不是颜色，而是高度值：

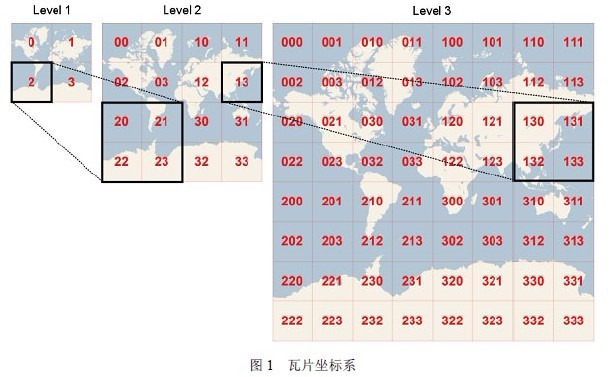
如同可见，子类切片的像素大小和父类是一样的，一般都是256*256的切片，但具体到地理范围上则只有父类的四分之一，所以顾名思义是四叉树。这样，从父类到子类放大的过程中，父类的一个像素，在子类中占了4个像素。也就是一个1：4的映射关系。尽管像素都是整数的，但我们在插值的过程中会有一个亚像素的概念。这样，同一个位置，经纬度都是相同的，但在子类和父类中的uv是不一样的，在对子类的遍历中，获取同一个经纬度对应父类uv的位置，进而得知在父类中相邻的四个像素和权重，进而插值获取其高度（颜色），如下是一个示意代码：

function interpolateMeshHeight(){

    var fromWest = (longitude - sourceRectangle.west) * (width - 1) / (sourceRectangle.east - sourceRectangle.west);

    var fromSouth = (latitude - sourceRectangle.south) * (height - 1) / (sourceRectangle.north - sourceRectangle.south);

    var widthEdge = (skirtHeight > 0) ? width - 1 : width;

    var westInteger = fromWest | 0;

    var eastInteger = westInteger + 1;

    if (eastInteger >= widthEdge) {

        eastInteger = width - 1;

        westInteger = width - 2;

    }

    var dx = fromWest - westInteger;

    return southwestHeight + (dX * (northeastHeight - northwestHeight)) + (dY * (northwestHeight - southwestHeight))

}

QuantizedMeshTerrainData.prototype.upsample

高度图毕竟还都是离散的点值，并没有构网，因而节点之间还没有建立关联，差值算法也相对容易一些。而STK的数据，本身已经是TIN的三角网结构了。这时，在父类中切割出四分之一来就有点复杂了。再打个比方，如果高度图相当于一个棋盘上均匀的大米，然后你四等分，取走其中的一份，而TIN三角网则相当于一个错综复杂的下水管，你要切走四分之一。这要怎么做到呢。假设此时我们有一把利刃，把这个TIN网格横一刀竖一刀，这时，我们迅速的把漏水的管道密封（形成新的节点），这样就实现了TIN三角网重采样的过程。

当然，这个过程相比高度图要复杂的多，因此Cesium中创建了Worker线程，切割的过程都是在线程中完成。具体到算法则如下：

for (i = 0; i < parentIndices.length; i += 3) {

    var i0 = parentIndices[i];

    var i1 = parentIndices[i + 1];

    var i2 = parentIndices[i + 2];

    var u0 = parentUBuffer[i0];

    var u1 = parentUBuffer[i1];

    var u2 = parentUBuffer[i2];

    triangleVertices[0].initializeIndexed(parentUBuffer, parentVBuffer, parentHeightBuffer, parentNormalBuffer, i0);

    triangleVertices[1].initializeIndexed(parentUBuffer, parentVBuffer, parentHeightBuffer, parentNormalBuffer, i1);

    triangleVertices[2].initializeIndexed(parentUBuffer, parentVBuffer, parentHeightBuffer, parentNormalBuffer, i2);

    // Clip triangle on the east-west boundary.

    var clipped = Intersections2D.clipTriangleAtAxisAlignedThreshold(halfMaxShort, isEastChild, u0, u1, u2, clipScratch);

    // Get the first clipped triangle, if any.

    clippedIndex = 0;

    if (clippedIndex >= clipped.length) {

        continue;

    }

    clippedIndex = clippedTriangleVertices[0].initializeFromClipResult(clipped, clippedIndex, triangleVertices);

    if (clippedIndex >= clipped.length) {

        continue;

    }

    clippedIndex = clippedTriangleVertices[1].initializeFromClipResult(clipped, clippedIndex, triangleVertices);

    if (clippedIndex >= clipped.length) {

        continue;

    }

    clippedIndex = clippedTriangleVertices[2].initializeFromClipResult(clipped, clippedIndex, triangleVertices);

    // Clip the triangle against the North-south boundary.

    clipped2 = Intersections2D.clipTriangleAtAxisAlignedThreshold(halfMaxShort, isNorthChild, clippedTriangleVertices[0].getV(), clippedTriangleVertices[1].getV(), clippedTriangleVertices[2].getV(), clipScratch2);

    if(clipped2.length == 10 && clipped.length == 10)

        var i = 10;

    addClippedPolygon(uBuffer, vBuffer, heightBuffer, normalBuffer, indices, vertexMap, clipped2, clippedTriangleVertices, hasVertexNormals);

    // If there's another vertex in the original clipped result,

    // it forms a second triangle.  Clip it as well.

    if (clippedIndex < clipped.length) {

        clippedTriangleVertices[2].clone(clippedTriangleVertices[1]);

        clippedTriangleVertices[2].initializeFromClipResult(clipped, clippedIndex, triangleVertices);

        clipped2 = Intersections2D.clipTriangleAtAxisAlignedThreshold(halfMaxShort, isNorthChild, clippedTriangleVertices[0].getV(), clippedTriangleVertices[1].getV(), clippedTriangleVertices[2].getV(), clipScratch2);

        addClippedPolygon(uBuffer, vBuffer, heightBuffer, normalBuffer, indices, vertexMap, clipped2, clippedTriangleVertices, hasVertexNormals);

    }

}

这个算法有点复杂，但思路清楚了，也就迎刃而解。首先，遍历顶点索引，每次+3，因为三个点构成一个三角形，所以完成了对所有三角网遍历切割的过程。在每次循环中，u0,u1,u2是三角形对应的三个点，然后通过Intersections2D.clipTriangleAtAxisAlignedThreshold实现三角形的切割算法。

这个切割的过程其实就是三角形和直线求交的过程，但更直观一些，因为这个直线是竖直或水平的，如果直线和三角形没有交点，那表示该三角形要么全在子类，要么全不在，不需要切割，我们不讨论这种情况。如果相交，则有两种情况：

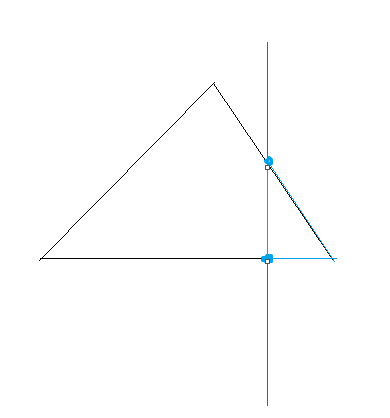
第一种情况，只保留了原三角形一个顶点，但会产生两个新的节点（蓝色），最终形成一个三角形。针对这种情况，我们在做一次水平的切合（水平线和蓝色三角形的相交计算），这个算法是一致的。

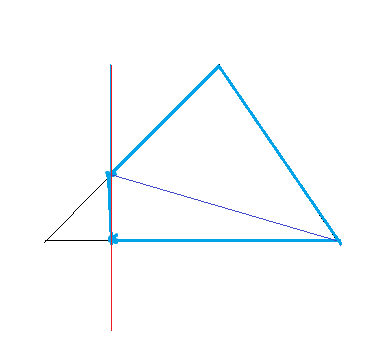
第二种情况，保留了原三角形两个顶点，同时也产生了两个新的节点（必然是偶数节点，哥尼斯堡七桥问题），这时，会形成两个三角形，则我们需要对这两个三角形单独做一次水平切割。

经过如上的逻辑，我们就完成了一个三角形的两刀切，当然，算法只提供了一个思路，并没有考虑特殊情况，正好经过顶点对半切，这个在实际中需要做一次额外的判断，避免少算或重复算。细的说里面有两个过程，求交点，构造新的三角形，分别通过clipTriangleAtAxisAlignedThreshold和addClippedPolygon函数实现。这时，如是是第二种情况，则还有一个三角形需要进行水平的切割和构造新三角形的过程。这是为什么会多一个if判断。

如上，新的，经过重采样的TIN三角网构建完成，Cesium会先渲染这个略微粗糙的地形，等待精细的地形下载完后在更新。当然，通过这个过程，我们能意识到，Cesium并不硬性的要求每一个地形Tile都能够获取到，如果其中一个Tile没有下载到（网络异常或环境限制），也能很好的自适应，而且也不方案该Tile的子类也可以正常渲染和更新。但前提是，根节点的地形数据是必须的。不管是蛋生鸡还是鸡生蛋，你总得现有一样。