Figures Inscribed in Curves （曲线上的图形）

Figures Inscribed in Curves\text{Figures Inscribed in Curves}Figures Inscribed in Curves

A short tour of an old problem

by Mark J. Nielsen (Professor of Mathematics, University of Idaho)

These pages give a brief and informal introduction to one of my favorite unsolved mathematics problems – the so-called “inscribed squares problem”. The question can be informally stated as follows:

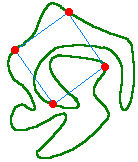
If you draw a curve on a piece of paper that ends where it began but never crosses itself (such as the green curve at right), will it always pass through the four corners of some square?

Notice that we don’t care whether or not the square “stays inside” of the curve – in fact, its sides may cross the curve many times. Nor do we care whether or not the corners of the square appear on the curve in any particular order.

A more exact statement of the question requires a couple of (fairly simple) definitions.

A simple closed curve is the image in the plane R2 of a continuous function f: [0,1] ----> R2 that is one-to-one except that f(0) = f(1).

Intuitively, this is exactly what you’d expect a “closed curve” to be – you start drawing at some point and trace a curve without lifting your pencil from the paper and without making your curve cross itself, ending at the point where you began. The word “simple” refers to the fact that the curve doesn’t cross itself.

Let J be a simple closed curve. We’ll say that a polygon P is inscribed in J if its vertices lie on J.

The inscribed squares problem can now be stated efficiently as:

Does every simple closed curve have an inscribed square?

To me, this is an appealing problem for several reasons:

• It is easy to state and understand the question.
• It has a nice geometric flavor (with a touch of topology for interest).
• It has avoided a complete solution for a long time.

The problem was first posed by Toeplitz in 1911, and while many interesting partial and related results have been given, no one knows the answer to the question above. In fact, the “range of ignorance” with regard to this question is quite astounding! For all the work that has been done on this question, we don’t yet know enough to rule out either of the following extreme possibilities:

• Possibility One: Every closed and bounded set that separates the plane into more than one piece must contain the four vertices of a square.
• Possibility Two: “Most” simple closed curves do not have inscribed squares. (By this we mean that if you were to draw a simple closed curve at random from the set of all simple closed curves, the probability that you’d get one with an inscribed square is zero. This notion can be made exact in several different ways, all of which involve details that we don’t want to get into here!)

Given that we can’t rule out either of these extremes, how much is known? Some of the first efforts to answer the question resulted in proofs that all polygons, differentiable curves, and curves bounding convex regions had inscribed squares. The best result to date is probably the following theorem (1989) due to Walter Stromquist.

Stromquist’s Theorem: If the simple closed curve J is “nice enough” then it has an inscribed square.

[Walter Stromquist, Inscribed squares and square-like quadrilaterals in closed curves, Mathematika 36: 187-197 (1989).]

Here, “nice enough” means the following: for each point P on the curve there must be a coordinate system for the plane in which some piece of the curve containing P is the graph y = f(x) of a continuous function.

At least one prominant mathematician I have met believes that Stromquist’s theorem is good enough to make the statement “All simple closed curves have inscribed squares” morally true – presumably because any curve you could actually draw with pencil and paper is nice enough to be covered by Stromquist’s theorem. In other words, this theorem more-or-less settles the informal version of our original question – any curve you draw on a sheet of paper will have an inscribed square. But the more formal version of the question is far from settled, because “most” simple closed curves have fractal-like behavior and are not “nice” at all. And while it is certainly good to have an answer for the pencil-and-paper version, the topologist in me cares about those curves that exist only in our imaginations. The universe of mathematics is much larger than just what we can draw on paper – if there are curves that don’t admit inscribed squares, I want to know about them.

Note: The following strategy may have occured to you as a possible way to get an inscribed square in an arbitrary (probably not-very-nice) curve J:

• Approximate J by a sequence of “nice” curves (such as polygons) P1, P2, P3, . . .
• Use Stromquist’s Theorem to get a square Qi inscribed in each Pi.
• Take a limit of the squares Q1, Q2, Q3, . . . (or more properly of some subsequence of this sequence of squares) to get a square inscribed in J.

This actually works perfectly well with one small but crucial catch: we can’t guarantee that the sizes of the squares Q1, Q2, Q3, . . . don’t go to zero in the limit. If that happens then the limiting figure is a degenerate square – in other words a single point! (And proving that every simple closed curve contains an inscribed point is not very interesting!) Because of this, any theorem that guarantees an inscribed figure of some minimal size would be extremely important. If we could improve Stromquist’s Theorem to say that “nice” curves have “big” inscribed squares, we’d have the whole matter settled.

But even if we are never able to ultimately answer the big question (which, by the way, I believe we will be able to do!), investigating the inscribed squares problem has led to many interesting side results. Below you will find links to six of these. I have chosen them for the simplicity and/or appeal of their proofs, which you can read by clicking on the theorem name. I have stated the theorems and proofs in their simplest, most intuitive versions, leaving off the messy details that are often necessary to state and prove a theorem in its most general form. If you want all the details, the reference to the relevant research paper is provided.

The first theorem shows that the “nice” behavior demanded by Stromquist’s Theorem can be replaced by symmetry – a different type of “nice” behavior. You will notice in the proof that the symmetry property reduces the number of points to be located on the curve from four to two.

• THEOREM A: Every simple closed curve that is symmetric about the origin has an inscribed square.

[Mark J. Nielsen and S.E. Wright, Rectangles inscribed in symmetric continua, Geometriae Dedicata 56: 285-297 (1995).]

The next two theorems don’t require any special behavior on the part of the curve, but also don’t quite guarantee inscribed squares. Instead, they say we can always find inscribed four-sided figures that are related to squares.

• THEOREM B: Every simple closed curve has lots of inscribed parallelograms and lots of inscribed rhombuses.

[Mark J. Nielsen, Rhombi inscribed in simple closed curves, Geometriae Dedicata 54: 245-254 (1995).]

• THEOREM C: Every simple closed curve has at least one inscribed rectangle.

[Proof due to Vaughan, included in the paper Balancing acts, Topology Proc. 6: 59-75 (1981) by Mark D. Meyerson.]

Finally, many interesting results can be proved about triangles inscribed in curves. This is, of course, a bit easier to deal with than squares, since the number of points to grapple with is only three.

• THEOREM D: If J is any simple closed curve and T is any triangle then J has an inscribed triangle similar to T.

[Mark D. Meyerson, Equilateral triangles and continuous curves, Fund. Math. 110: 1-9 (1980).]

• THEOREM E: Extending Theorem D, J has so many inscribed triangles similar to T that the vertices of all these inscribed triangles are “dense” in the curve J.

[Mark J. Nielsen, Triangles inscribed in simple closed curves, Geometriae Dedicata 43: 291-297 (1992).]

• THEOREM F: If T is any triangle and if J is a simple closed curve in 3-dimensional space R3 (instead of in the plane) that is differentiable (has a tangent line) at at least one point, then J has an inscribed triangle similar to T.

[Eric Rawdon and Jonathan Simon, unpublished(?) – correspondence with Professor Victor Klee.]

If you like geometry, you may enjoy reading a few of the proofs of the above theorems (just follow the links). For a more thorough introduction to the inscribed squares problem, as well as many more references to related papers, consult pp.58-65 and 137-144 in the excellent book Old and New Unsolved Problems in Plane Geometry and Number Theory (1991, Mathematical Association of America) by Victor Klee and Stan Wagon.

You may even feel inspired to try your own hand at chipping away toward a solution to the inscribed squares problem. Below you will find a few exercises to get you warmed-up, followed by some open-ended (and as-yet-unanswered) questions. Good luck – as they say in TV’s The X-files, “the truth is out there somewhere.”