Codeforces Round #589 (Div. 2)-E. Another Filling the Grid-容斥定理

Codeforces Round #589 (Div. 2)-E. Another Filling the Grid-容斥定理

---

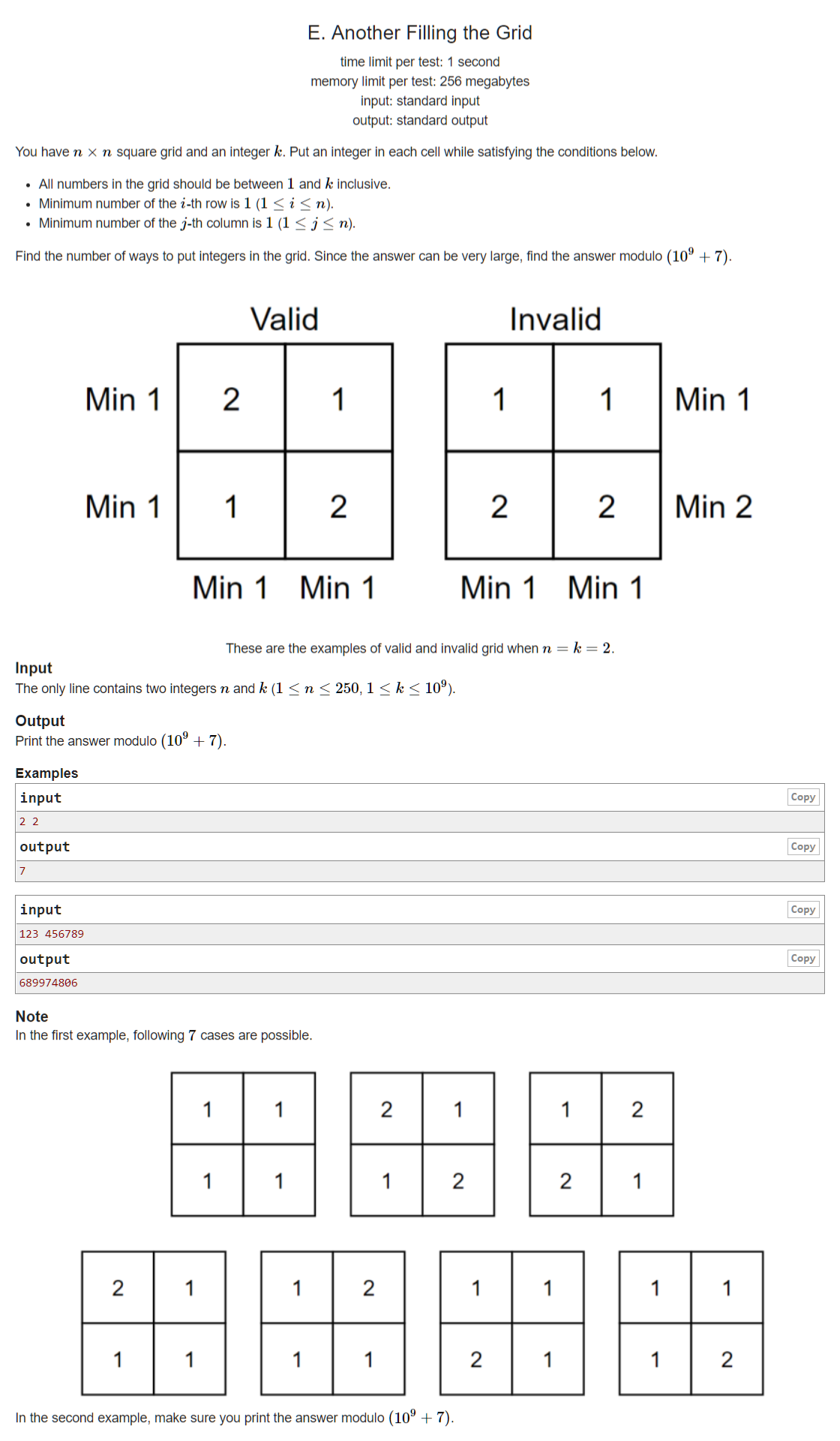
【Problem Description】

在\(n\times n\)的格子中填入\([1,k]\)之间的数字，并且保证每一行至少有一个\(1\)，每一列至少有一个\(1\)，问有多少种满足条件的填充方案。

【Solution】

令\(R[i]\)表示为第\(i\)行至少有一个\(1\)的方案数，\(C[i]\)表示第\(i\)列至少有一个\(1\)的方案数。则题目要求的就是\(\bigcap_{i=1}^nR[i]\cap C[i]\)。由容斥定理得：

\[\sum_{i=0}^{n} \sum_{j=0}^{n} (-1)^{i+j} \cdot {n\choose j} \cdot {n\choose i} \cdot k^{n^2 - n \cdot (i+j) + i \cdot j} \cdot (k-1)^{n \cdot (i+j) - i \cdot j}
\]

表示从\(n\)行中，选\(i\)行，从\(n\)列中选\(j\)列，选出\(n\cdot(i+j)-i\cdot j\)个格子不能放\(1\)，这些格子有\((k-1)^{n\cdot (i+j)-i\cdot j}\)种放置方案，剩余的\(n^2-n\cdot (i+j)+i\cdot j\)有\(k^{n^2-n\cdot (i+j)+i\cdot j}\)种放置方案。

---

【Code】

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef int Int;
#define int long long
#define maxn 1005
#define INF 0x3f3f3f3f
const int mod=1e9+7;
int bit[maxn][maxn];
int fpow(int a,int b){
	int ans=1;a%=mod;
	while(b){
		if(b&1) (ans*=a)%=mod;
		(a*=a)%=mod;
		b>>=1;
	}
	return ans;
}
Int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n,k;cin>>n>>k;
	for(int i=0;i<=n;i++) bit[i][0]=1;
	for(int i=1;i<=n;i++){ //预处理组合数
		for(int j=1;j<=i;j++){
			bit[i][j]=(bit[i-1][j]+bit[i-1][j-1])%mod;
		}
	}
	int ans=0;
	for(int i=0;i<=n;i++){ //直接套公式即可
		for(int j=0;j<=n;j++){
			ans+=((i+j)&1?-1:1)*bit[n][i]%mod*bit[n][j]%mod*fpow(k,n*n-n*(i+j)+i*j)%mod*fpow(k-1,n*(i+j)-i*j)%mod;
			ans%=mod;
		}
	}
	cout<<(ans+mod)%mod<<endl;
	return 0;
}