LCA的多种求法（超详细！！！）

倍增求LCA

(1)树上倍增法 预处理

设f[x,k]表示x的2^k辈祖先,即从x向根节点走2^k步到达的节点。特别地,若该节点不存在,则令f[x,k]=0。f[x,0]就是x的父节点。可以得出f[x][k]=f[f[x][k-1]][k-1]。

我们可以对树进行遍历,由此得到f[x,0]，再计算f数组所有值。

以上部分是预处理,时间复杂度为O(nlogn)。之后可以多次对不同的x,y计算LCA,每次询问的时间复杂度为O(logn)。

【代码实现】 预处理
void dfs(int u,int father) 
{
    Dep[u]=Dep[father]+;    
    for(int i=;i<=;i++)
    {
    if(!f[u][i)break;
    else f[u][i+]=f[f[u][i]][i];  
    }
    for(int e=first[u],v; v=go[e],e; e=next[e])    
    {        
        if(v==father) continue;    
        f[v][]=u;                       //v向上跳2^0=1就是u    
        dfs(v,u);    
    }    
} 

（2）基于f数组计算LCA(x,y)

分为以下几步:

1.设dep[x]表示x的深度。不妨设dep[x]≥dep[y](否则可交换x,y)。

2.用二进制拆分思想,把x向上调整到与y同一深度。具体来说,就是依次尝试从x向上走k= 2logn,…,21,20步,若到达的节点比y深,则令x=f[x,k]。

3.若此时x=y,说明已经找到了LCA,LCA就等于y。

4.若此时x≠y，依次尝试把x,y同时向上走 k= 2logn,…,21,20步,若f[x,k]≠f[y,k](即仍未相会),则令x=f[x,k],y=f[y,k]。

5.此时x,y必定只差一步就相会了,它们的父节点f[x,0]就是LCA。

【代码实现】 查询x,y的LCA
int LCA(int x,int y)                   
{    
    if(Dep[x]<Dep[y]) swap(x,y);  //让x深度较大   
    for(int i=;i>=;i--)        //先将x,y跳到一个深度，一定要倒着for    
      if(Dep[f[x][i]]>=Dep[y]) x=f[x][i];  //先跳到同一层    
    if(x==y) return x;           //如果相等直接返回
    for(int i=;i>=;i--)       //此时x,y已跳到同一层   
        if(f[x][i]!=f[y][i])     //如果f[x][i]和f[y][i]不同才跳  
          x=f[x][i],y=f[y][i];  
    return f[x][];       //x,y是深度最浅且不同的点，即lca的子结点 
} 

树链剖分求LCA

将静态树上的点按某种方式组织起来，剖分成为若干条链，形成若干个序列，则操作路径就会被拆分为几条链，也就是若干个完整序列

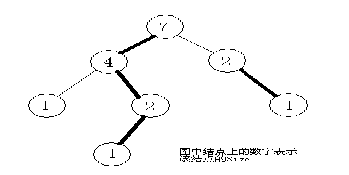
轻重边剖分： 我们将树中的边分成重边和轻边。如下图，加粗的边是重边，其余是轻边。 我们可以以任意点为根，然后记size[u]为以u为根的子树的结点个数，令 为v所有儿子中size值最大的一个儿子，则(u,v)为重边,v称为u的重儿子。 到其余儿子的边为轻边。

轻重边剖分的过程可以使用两次dfs来实现。

剖分过程中要计算如下5个值：

f[x]:x在树中的父亲

size[x]:x的子树结点数(子树大小)

dep[x]:x在树中的深度

son[x]:x的重儿子，即为重边

top[x]:x所在重路径的顶部结点(深度最小)

第一遍dfs计算前4个值， 第二遍dfs计算后1个值。

查询LCA:

1、找到x、y所在的链头

2、如果两个链头不相等，则选择链头深度大的往上跳

3、最后两个链头相等，说明在同一条重路径上，深度浅的就是LCA

看到这里勤奋好学的你一定已经摩拳擦掌、跃跃欲试了吧

那么我们来做一道简单的模板题

【例 1】点的距离

【题目描述】

给定一棵 n 个点的树，Q 个询问，每次询问点 x 到点 y两点之间的距离。

【输入】

第一行一个正整数 n，表示这棵树有 n 个节点； 接下来 n−1 行，每行两个整数 x,y表示 x,y 之间有一条连边； 然后一个整数 Q，表示有 Q个询问； 接下来 Q行每行两个整数 x,y 表示询问 x 到 y 的距离。

【输出】

输出 Q 行，每行表示每个询问的答案。

【输入样例】

6 1 2 1 3 2 4 2 5 3 6 2 2 6 5 6

【输出样例】

3 4

---（QAQ格式的问题我真的搞不nai）

---

解法一：倍增

解法二：树链剖分

如果还想进一步了解运用LCA，亲亲，这边建议您可以去AC这两道题题哦~

这是一个传送门...传送门2（才不是没有灵魂的可爱传送门呢QWQ）

蟹蟹资瓷，请顺手点个“推荐”吧~mua(づ￣3￣)づ╭❤～

（2019/8/17更：还想再bb一句，传送门什么的太累了不想做了，还是去首页找找吧，在标签里看“LCA”或者“树上倍增法”应该会有你想要的