浅入深出ETCD之【raft原理】

前言

这次我们来说说，有关于etcd原理的一些事情。之前我们已经了解到了etcd是一个分布式的k-v存储，那么它究竟是如何保证数据是如何复制到每个节点上面去的呢？又是如何保证在网络分区的情况下能正常工作下去？raft协议到底是什么？带着这些问题我们继续往下看。

raft选举策略

我们知道etcd使用raft协议来保证整个分布式的节点网络能正常的运转并且能正确的将数据复制到每个节点上面去。那么什么是raft协议嘞？

首先我们有这样一个背景：raft是想维护整一个网络，其中有一个领导人，这个领导人负责将收到的信息同步给网络中的其他所有节点，从而保证整个网络数据一致。

如果你有一定的英文基础，我建议直接查看下面这个网站，它用动画非常清楚的描述了raft选举的整个过程：http://thesecretlivesofdata.com/raft/

这个其实已经说明的超级棒了，如果你还看不懂，我下面会用最简单的几个要点来进行最简单的说明。

大多数理论

首先说明一个理论，叫做大多数理论，很简单，举个栗子：

有10个人，如果你将苹果给其中的6个人（大多数），那么你随机选择5个人，一定有一个人会有苹果。

在etcd中的应用：

选举中只要有大多数（超过半数的人给你投票）你肯定就是票数最多的了，不可能有人比你更多。
只需要将日志复制给大多数的节点，那么只要有一半的节点正常工作就能保证数据最新

选举状态

下面是一些选举过程中节点的状态
leader 表示选举最终产生的领导人
candidate 候选状态，表示当前正在参与选举
follower 表示选举最终自己不是领导人，那自己就是从属节点

选举过程与要点

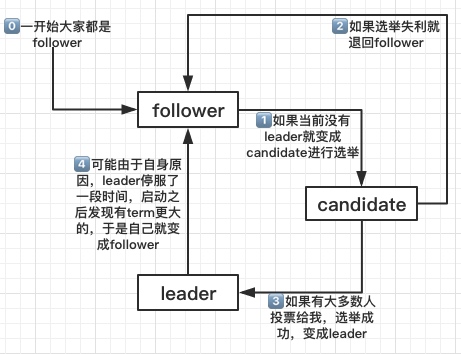
所有节点一开始都是follower状态
当节点处于follower状态时，每个节点随机经过一段时间，如果没有收到leader的消息就会进入candidate状态（证明当前没有leader节点需要重新进行选举），如果收到信息就会继续保持follower状态
当节点处于candidate就会要求别人给自己投票，收到大多数的节点的投票那就转变为leader状态，否则要么是别的节点成为了leader，要么就是因为特殊情况导致这次选举失败重新进行选举
每次选举举办的时候有一个term，在每一个term中，每个节点只能投票一次
投票的时候必须投给当前数据至少和自己一样的节点，并且term大的优先

日志复制规则

etcd是通过日志复制来实现数据同步的

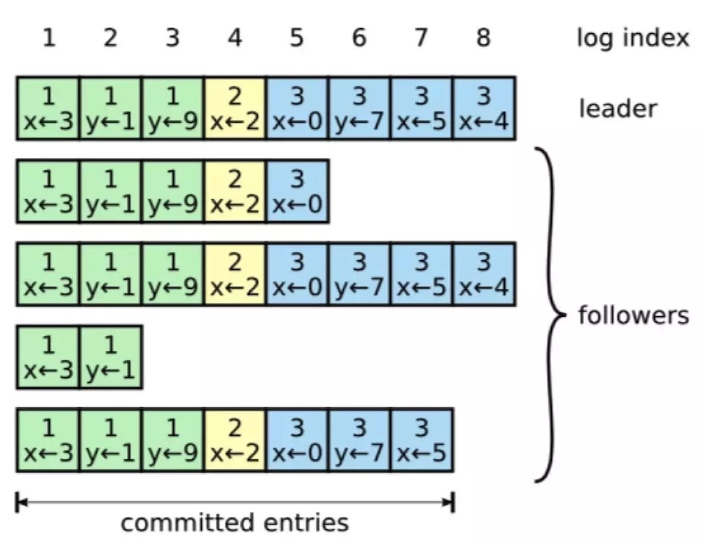
这个图网上也很多，说明的是日志复制的规则
每个节点都有一份自己的日志，有的节点多，有的节点少，日志最多的肯定是leader。
上图还有几个要点，我看别人没提到，我就提一下：

颜色代表term
第四行表示的这个节点，第一term下复制了两个日志就异常挂掉了
最终只有第三行这个follower和第一行的leader保持了同步

异常情况

raft之所以厉害因为即使出现一些特殊情况，整个网络在一定的时间之后也能自动恢复并正常工作。

一个节点的异常

首先最常见的情况就是一个节点出现异常，有可能是这个节点的服务器挂了，或者别的什么原因。

如果出现问题的这个节点是follower，那么没有关系，整个网络依旧能正常运行，当这个节点再次加入网络的时候也只需要同步后面的数据即可。
如果出现问题的是leader，有一点麻烦，因为网络中没有leader节点了，那么就会重新进行选举，重新找一个leader，当这个异常节点恢复之后发现当前网络中有leader了，而且term还比自己大，那么自己就退位称为follower。

网络分区

还有一种异常情况是由于网络导致的，网络出现异常，导致节点之间的通信存在异常，一部分节点与另一部分之间没有办法访问了。如下图所示：

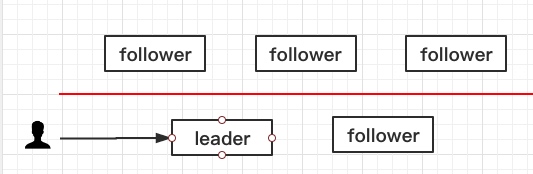
上面三个follower没有办法与下面的节点进行通信。

当客户端再次请求leader发送数据的时候，leader发现没有办法将数据同步给给大多数节点，它只能给自己和旁边的一个，此时leader没有办法给客户端反馈。
上面三个节点由于收不到leader的消息，那么会认为网络中没有leader存在，会重新进行选举操作，因为当前上面有三个节点存在（只要有超过半数的节点参与选举就行），所以可以重新选举成功，选出新的leader告诉客户端，客户端就会重新发送数据到新的leader。
当网络恢复之后又会找到最新的leader从而将数据同步至最新的状态。

总结

总的来说，只要整个网络中存在大多数节点正常运行，那么etcd就是可用的，并且能够保证数据正确。当网络恢复之后也能将数据调整到最新的状态。
raft强大的地方在于它能自动的进行状态的变化，自动进行选举，并且选举遵循一定的策略，进而保证整个网络的正常运转。同时保证数据的一致性。
了解etcd的这个原理有助于我们后续的使用以及源码的阅读。