[LeetCode] 119. Pascal's Triangle II 杨辉三角之二
Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal's triangle.
Note that the row index starts from 0.

In Pascal's triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 3
Output: [1,3,3,1]
Follow up:
Could you optimize your algorithm to use only O(k) extra space?
杨辉三角想必大家并不陌生,应该最早出现在初高中的数学中,其实就是二项式系数的一种写法。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
杨辉三角形第n层(顶层称第0层,第1行,第n层即第 n+1 行,此处n为包含0在内的自然数)正好对应于二项式 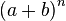 展开的系数。例如第二层 1 2 1 是幂指数为2的二项式
展开的系数。例如第二层 1 2 1 是幂指数为2的二项式 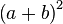 展开形式
展开形式 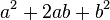 的系数。
的系数。
杨辉三角主要有下列五条性质:
- 杨辉三角以正整数构成,数字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
 行的数字个数为
行的数字个数为 个。
个。 - 第
 行的第
行的第 个数字为组合数
个数字为组合数 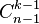 。
。 - 第
 行数字和为
行数字和为 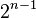 。
。 - 除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第
 行第
行第 个数字等于第
个数字等于第  行的第
行的第  个数字与第
个数字与第 个数字的和)。这是因为有组合恒等式:
个数字的和)。这是因为有组合恒等式: 。可用此性质写出整个杨辉三角形。
。可用此性质写出整个杨辉三角形。
由于题目有额外限制条件,程序只能使用 O(k) 的额外空间,那么这样就不能把每行都算出来,而是要用其他的方法, 我最先考虑用的是第三条性质,算出每个组合数来生成第n行系数,代码请参见评论区一楼。本地调试输出前十行,没啥问题,拿到 OJ 上测试,程序在第 18 行跪了,中间有个系数不正确。那么问题出在哪了呢,仔细找找,原来出在计算组合数那里,由于算组合数时需要算连乘,而整型数 int 的数值范围只有 -32768 到 32768 之间,那么一旦n值过大,连乘肯定无法计算。而丧心病狂的 OJ 肯定会测试到成百上千行,所以这个方法不行。那么我们再来考虑利用第五条性质,除了第一个和最后一个数字之外,其他的数字都是上一行左右两个值之和。那么我们只需要两个 for 循环,除了第一个数为1之外,后面的数都是上一次循环的数值加上它前面位置的数值之和,不停地更新每一个位置的值,便可以得到第n行的数字,具体实现代码如下:
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> res(rowIndex + );
res[] = ;
for (int i = ; i <= rowIndex; ++i) {
for (int j = i; j >= ; --j) {
res[j] += res[j - ];
}
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/119
类似题目:
参考资料:
https://leetcode.com/problems/pascals-triangle-ii/
https://leetcode.com/problems/pascals-triangle-ii/discuss/38420/Here-is-my-brief-O(k)-solution
LeetCode All in One 题目讲解汇总(持续更新中...)
[LeetCode] 119. Pascal's Triangle II 杨辉三角之二的更多相关文章
- [LeetCode] 119. Pascal's Triangle II 杨辉三角 II
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- [LeetCode] Pascal's Triangle II 杨辉三角之二
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- Leetcode#118. Pascal's Triangle(杨辉三角)
题目描述 给定一个非负整数 numRows,生成杨辉三角的前 numRows 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 5 输出: [ [1], [1,1], [1,2, ...
- LeetCode 118. Pascal's Triangle (杨辉三角)
Given numRows, generate the first numRows of Pascal's triangle. For example, given numRows = 5,Retur ...
- LeetCode 119 Pascal's Triangle II
Problem: Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Ret ...
- Leetcode 119 Pascal's Triangle II 数论递推
杨辉三角,这次要输出第rowIndex行 用滚动数组t进行递推 t[(i+1)%2][j] = t[i%2][j] + t[i%2][j - 1]; class Solution { public: ...
- LeetCode 119. Pascal's Triangle II (杨辉三角之二)
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- leetcode 119 Pascal's Triangle II ----- java
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- Java [Leetcode 119]Pascal's Triangle II
题目描述: Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return ...
随机推荐
- Java-100天知识进阶-JVM内存-知识铺(三)
知识铺: 致力于打造轻知识点,持续更新每次的知识点较少,阅读不累.不占太多时间,不停的来唤醒你记忆深处的知识点. Java内存模型(JMM) JVM内存模式是JVM的内存分区 Java内存模式是一种虚 ...
- 你不得不知的Golang线程模型 [转载]
原著:翟陆续(加多) 资深Java , 著Java并发编程之美 一.前言 本节我们来探讨Go的线程模型,首先我们先来回顾下常见的三种线程模型,然后在介绍Go中独特的线程模型. 二.三种线程模型 线程的 ...
- centos6 cgroup及cgred简介和简单使用
一.cgroup简介 Linux CGroup全称Linux Control Group, 是Linux内核的一个功能,用来限制,控制与分离一个进程组群的资源(如CPU.内存.磁盘输入输出等).这个项 ...
- [Flutter] Windows桌面程序开发
在今年5月的谷歌I/O 2019大会时, 谷歌就宣布了flutter已经支持全平台开发, 包括 android, ios, mac, linux, windows, web 等 . Flutter桌面 ...
- 【RT-Thread笔记】IO设备模型及GPIO设备
RTT内核对象--设备 RT-Thread有多种内核对象,其中设备device就是其中一种. 内核继承关系图如下: 设备继承关系图如下: device对象对应的结构体如下: 其中,设备类型type有如 ...
- 关联mysql失败_Server returns invalid timezone. Go to 'Advanced' tab and set 'serverTimezon' 时区错误
时区错误,MySQL默认的时区是UTC时区,比北京时间晚8个小时. 所以要修改mysql的时长 在mysql的命令模式下,输入: set global time_zone='+8:00'; 再次连接成 ...
- 2019-07-23 类的继承和final关键字的应用
我们称以存在的用来派生新类的类为基类,又称做父类,超类.由已存在的类派生出的新类称为派生类,又称为子类.从一个基类派生的继承称单继承,从多个基类派生的继承称为多继承.也就是说:一个类只能直接从一个类中 ...
- AT+CNUM获取不到手机号
原因是卡商没有写入SIM卡 解决办法 手动写入 1. 先确认SIM卡的本机号码 2. 选择电话本存储 /* AT+CPBS Select phonebook memory storage " ...
- springBoot添加日志管理
一. 近期自己的项目想要一个记录日志的功能,而springboot本身就内置了日志功能,然而想要输入想要的日志,并且输出到磁盘,然后按天归档,或者日志的切分什么的,自带的日志仅仅具有简单的功能,百度了 ...
- updataStateByKey算子的使用
updataStateByKeyApp.scala import org.apache.spark.SparkConf import org.apache.spark.streaming.{Secon ...
