2018SCin tsyzDay2 模拟赛-动态规划（简单的）

内心OS：简单？？？？？还是我太弱了。

期望得分：100+100+0+0+0+0+随机暴力的点==200

实际得分：0+100+10+0+10+0==120

您知道我第一题为什么错了嘛？？文件在混乱中被我注释掉了

mmp.

T1

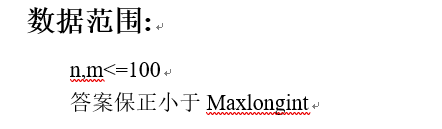
三月份考过这道题--记忆化搜索。

还写过题解，提醒这里样例给错了orz。

放上链接QAQ   http://www.cnblogs.com/nopartyfoucaodong/p/8589116.html

和滑雪一样，听说这是一道棋盘dp？ 不解。

§ 注意边界的处理，防止越界。
§ 因为是跳的次数，所以最后要减一。

code

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 int n,m,ans;
 int dx[]={-,,,};
 int dy[]={,,-,};
 int w[][];
 int f[][];
 int memory_search(int x,int y)
 {
     if(f[x][y]) return f[x][y];
     int tmp=;
     for(int i=;i<;i++)
     {
           int tx=x+dx[i];int ty=y+dy[i];
           if(w[tx][ty]>w[x][y]&&tx>=&&tx<=n&&ty>=&&ty<=m) tmp=max(memory_search(tx,ty)+,tmp);
     //      else continue;
     }
     f[x][y]=tmp;
     return f[x][y];
 }
 int main()
 {
     freopen("1.in","r",stdin);
     freopen("1.out","w",stdout);
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
      for(int j=;j<=m;j++)
        scanf("%d",&w[i][j]);
     for(int i=;i<=n;i++)
      for(int j=;j<=m;j++)
        ans=max(ans,memory_search(i,j));
     printf("%d",ans+);
     fclose(stdin);
     fclose(stdout);
     return ;
 }

T2

二进制优化多重背包裸题，二月考过。

T3

noip能量项链原题。

https://www.luogu.org/problemnew/show/P1063

Chemist没有做过能在考场上1A，%一%！！！

加强了对区间dp的理解！

一般地，我们在求解区间型动态规划时，会把一个个区间作为各个阶段。

一般地，需要用到三层循环进行枚举，外层为区间长度，其次为端点，最内层为断点。

另外，本题还需要断环成链，开long long。

code

 #include<cstdio>
 #include<algorithm>

 using namespace std;
 typedef long long ll;

 int n;
 ll a[];
 ll ans,f[][];

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         scanf("%d",&a[i]);
         a[i+n]=a[i];
     }
     for(int len=;len<=n+;len++)
      for(int i=;i+len-<=*n;i++)
      {
          int j=i+len-;
          for(int k=i+;k<=j-;k++)
          f[i][j]=max(f[i][j],f[i][k]+f[k][j]+a[i]*a[k]*a[j]),ans=max(ans,f[i][j]);
      }
     printf("%lld",ans);
     //fclose(stdin);
     //fclose
     return ;
 } 

T4

是一道典型的动态规划。

状态设计：  f[i][j]表示在前i个数中取j个的和的最大值。

《初始化1》我们从数据中可以发现，序列是有负数的。所以我们初始要把f数组和ans设为负无穷。

但是我们鬼畜地发现，用for循环不能进行初始化，必须得用memset（QAQ为什么呀）

memset(f,,sizeof(f))

这句可以赋为负无穷，0x3f可以赋为正无穷。

《初始化2》

对f数组进行初始化：在j为1时，不受选的个数限制。

for(int i=;i<=n;i++)
  for(int j=;j<=m;j++)
    f[i][]=max(f[i-][],a[i]);

转移方程：

f[i][j]=max( f[i-k][j-1]+a[i]  【取，受i>=k的限制】， f[i-1][j] 【不取】 ）

code

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<algorithm>

 using namespace std;

 int n,m,k,ans=-0x7fffffff;
 int a[],f[][];

 int main()
 {
     freopen("4.in","r",stdin);
     freopen("4.out","w",stdout);
     scanf("%d%d%d",&n,&m,&k);
     for(int i=;i<=n;i++) scanf("%d",&a[i]);
     //为什么for循环不行qaq
     //for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) f[i][j]=-0x7fffffff;
     memset(f,,sizeof(f));
     for(int i=;i<=n;i++)
      for(int j=;j<=m;j++)
       f[i][]=max(f[i-][],a[i]);
     for(int i=;i<=n;i++)
      for(int j=;j<=m;j++)
      {
           f[i][j]=max(f[i-][j],f[i][j]);
           if(i>=k) f[i][j]=max(f[i][j],f[i-k][j-]+a[i]);
      }
     printf("%d",f[n][m]);
     fclose(stdin);
     fclose(stdout);
     return ;
 }
  

T5

我们看一看官方的题解好了XD

感觉分析的很透彻呀

看完题目后，对题目分析可知，此题的最优解法就是动态规划。

当然，因为有两个坩锅，所以明显是一道双进程动态规划题目。因此，先用动态规划求解一个坩锅能达到的最大药效，把已用的药材去掉，再次动态规划的方法是不可行的！

1．分析最优子结构：

数据备注：

t1[i]表示第i种药材的起始时间

t2[i]表示第i种药材的结束时间

w[i]表示第i种药材的药效

time表示总时间 n表示药材总数

（为了让大家更好理解 先讲一种未优化的算法）

设动态规划数组 dp[i][j][k] 表示前i种药材放入两个坩锅，第一个坩锅达到时间j，第二个坩锅达到k时所能达到的最大药效。题目的解就是dp[n][time][time];

因为要知道在time时刻两个坩锅的效益和，则需要用到它的子结构的最优值。

分析子结构的最优值的取得条件：

对于第i种药材，放入两个坩锅，有三种处理方法：

1． 把它放入第一个坩锅；

2． 把它放入第二个坩锅；

3． 不放入任何坩锅

对1：

　　dp[i][j][k]=dp[i-1][t1[i]-1][k]+w[i];   条件：仅当j=t2[i];

对2：

　　dp[i][j][k]=dp[i-1][j][t1[i]-1]+w[i];   条件：仅当k=t2[i];

对3：

　　dp[i][j][k]=max{ dp[i-1][j][k],       无条件　　

　　dp[i][j-1][k],       条件 j>0

　　dp[i][j][k-1],       条件 k>0

因此 子结构dp[i][j][k]的取值就是对1，2，3种状态的最大值

即：

dp[i][j][k]=max{

　　dp[i-1][t1[i]-1][k]+w[i];   条件：仅当j=t2[i];      //  个人注释：减一的意思是在开始的前一秒

　　dp[i-1][j][t1[i]-1]+w[i];   条件：仅当k=t2[i];

　　dp[i-1][j][k],             无条件

　　dp[i][j-1][k],             条件 j>0

　　dp[i][j][k-1],             条件 k>0

}

 

2．解决后效性：

为了解决后效性，在这里，当且仅当j=t1[i]或k=t1[i]时，药材才会被放入坩锅内，且保证了同一种药品不会在以后被多次放入或者是同时放入二个坩锅，当然，仅仅是这样还是不能保证能求出最优解，因为在计算过程中，结构会被刷新，因此对于结束时间较晚的药材，若在结束时间较前的药材先被计算，则较前的药材就以为价值小而不会被记录，因此就应该在动态规划之前将数据按结束时间t2[i]升序排序。因此，我们完美的消除了后效性。

3.优化问题：

     1．时间复杂度的优化：

根据对称性，两个坩锅不计先后，且一摸一样，因此dp[i][j][k]等价于dp[i][k][j]，因此，在循环的时候可以令j<=k;然后加几个判断即可。具体方法不再赘述，请自行解决。

     2．空间复杂度的优化：

 在求解的过程中 即：dp[i][j][k]的值 只与 dp[i-1][…][…]的值有关，因此可以将数组降为2维 即：dp[j][k]，具体方法不再赘述。可以看标程，标程有两个，一个是优化过的，一个是未经过优化的。

因此，对于这道题目，

　　近似最优时间复杂度为O(n^3)

　　近似最优空间复杂度为O(n^2)

code

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 int T,n;
 int f[][];
 struct node{
     int t1,t2,w;
 }a[];

 bool cmp(node x,node y)
 {
     return x.t2<y.t2;
 }

 int main()
 {
     freopen("medic.in","r",stdin);
     freopen("medic.out","w",stdout);
     scanf("%d%d",&T,&n);
     for(int i=;i<=n;i++)
      scanf("%d%d%d",&a[i].t1,&a[i].t2,&a[i].w);
     sort(a+,a+n+,cmp);
     for(int i=;i<=n;i++)
      for(int j=T;j>=;j--)
       for(int k=T;k>=;k--)
        {
               if(j>=a[i].t2) f[j][k]=max(f[j][k],f[a[i].t1-][k]+a[i].w);
               if(k>=a[i].t2) f[j][k]=max(f[j][k],f[j][a[i].t1-]+a[i].w);
        }
     printf("%d",f[T][T]);
     fclose(stdin);
     fclose(stdout);
     return ;
 } 

小结，这几天做了好多动规（水题），遇到多维的时候，判断条件也会几层（循环层数），为了维持下去，可加入特判（如本题的if）