前k大金币(动态规划,递推)

/*
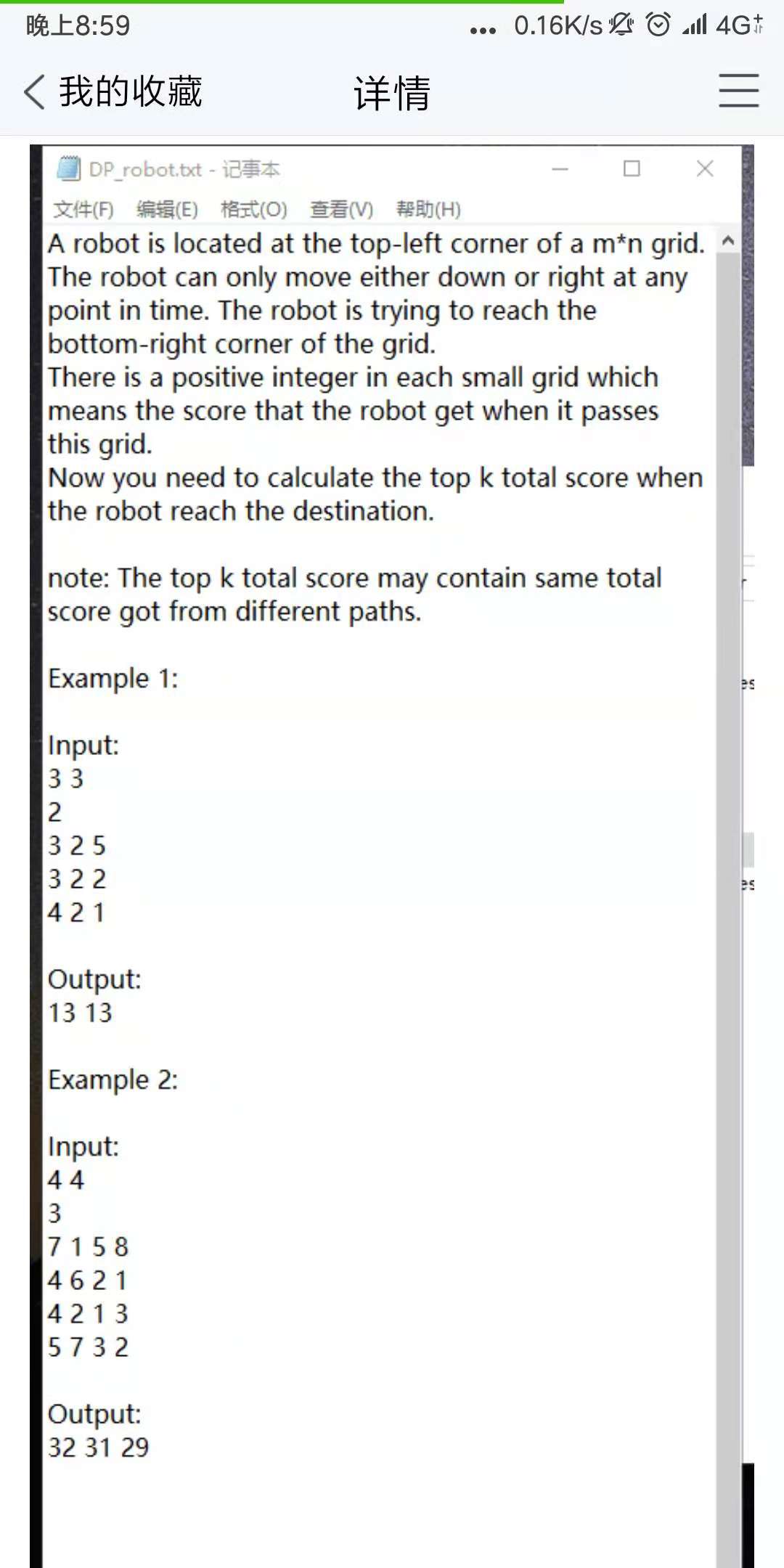
///题解写的很认真,如果您觉得还行的话可以顶一下或者评论一下吗?
思路:
这题复杂在要取前k大的结果,如果只是取最大情况下的金币和,直接
动态规划递归就可以,可是前k大并不能找出什么公式,所以在二元数组的基础上再并上一个vector
 
首先:初始化最左边和最上边(动态规划的边缘)
其次:找出关系,每个格的金币只可能来自上边或者右边(动态规划的状态方程)
然后:我们要找的是前k大金币总和而不是前1大,所以准备vector存更多情况
然后:每次处理时,当前格子除了拿上自己的金币外,还要接受前面或者上边送来
        的一袋袋金币这些金币,这些袋子有大有小,尽可能挑出前k大的袋子(如果没有
        k那么多就全部挑出来),然后当前格子最多接受k+k袋金币(上面的k和左边的k)
        接受时边接受边排序,那么下次当前格子附近的格子要调用这个格子的金币袋子
        情况时找出前k大即可
最后:f[m][n]这个最右下角的格子可能积累了一堆金币,从后往前(从大到小)挑出
        k个袋子即可
 
*/
//一个学长(栋神)出的题
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=;
vector<ll>f[maxn][maxn];//f向量用来存每个位置前k大的总金币
ll a[maxn][maxn];//a数组用来存入数据
int main()
{
///输入环节
    ll m,n,k;
    cin>>m>>n>>k;
    for(ll i=;i<=m;i++)
        for(ll j=;j<=n;j++)
            scanf("%lld",&a[i][j]);//输入金币情况
///处理环节
    f[][].push_back(a[][]);
        //先向f向量中添加初始金币
        //同样的,接下来两个for分别初始化向量左边和上面两个边界的金币数
    for(ll i=;i<=m;i++)
        f[i][].push_back(a[i][]+(f[i-][])[]);
    for(ll i=;i<=n;i++)
        f[][i].push_back(a[][i]+(f[][i-])[]);
        //因为到最左竖和最上横分别只有一条路径,所以很好处理
 
    ///接下来的向量f[i][j]会一直保持从小到大的排列顺序
    for(ll i=;i<=m;i++)
        for(ll j=;j<=n;j++)//两个for循环遍历剩下情况
        {
            //对f[i][j]的上面那格分析
            if(k<=f[i-][j].size())//如果要求的k比现在有的元素少
                //即如果k比当前vector内元素数目小的情况
            for(ll x=f[i-][j].size()-;x>=f[i-][j].size()-k;x--)
            {//从f[i-1][j]从后往前挑出k个数(也就是最大的k个数),分别加上a[i][j],塞入f[i][j]中
                //这让f[i][j]增加了新的元素,但f[i][j]依然是从小到大排序(为后面服务)
                (f[i][j]).insert(upper_bound(f[i][j].begin(),f[i][j].end(),(f[i-][j])[x]+a[i][j]),(f[i-][j])[x]+a[i][j]);
            }
            else//如果vector内元素数目小,还不够k多的情况
            for(ll x=f[i-][j].size()-;x>=;x--)
            {//同上
                (f[i][j]).insert(upper_bound(f[i][j].begin(),f[i][j].end(),(f[i-][j])[x]+a[i][j]),(f[i-][j])[x]+a[i][j]);
            }
            //对f[i][j]的左边那格分析
            ///第一个if else是配套的,只执行一个,这里又是一套if else,只执行一个
            //那么每次循环就处理一次上方,处理一次左边
            if(k<=f[i][j-].size())//类似于上面,不再叙述
            for(ll x=f[i][j-].size()-;x>=f[i][j-].size()-k;x--)
            {
                f[i][j].insert(upper_bound(f[i][j].begin(),f[i][j].end(),(f[i][j-])[x]+a[i][j]),(f[i][j-])[x]+a[i][j]);
            }
            else
            for(ll x=f[i][j-].size()-;x>=;x--)
            {
                f[i][j].insert(upper_bound(f[i][j].begin(),f[i][j].end(),(f[i][j-])[x]+a[i][j]),(f[i][j-])[x]+a[i][j]);
            }
        }
    for(ll i=f[m][n].size()-;i>=f[m][n].size()-k;i--)
        printf("%lld ",(f[m][n])[i]);
        //从后往前数k个数,分别输出(即在f[m][n]找出最大的k个数)
}