洛谷——P3576 [POI2014]MRO-Ant colony

P3576 [POI2014]MRO-Ant colony

题目描述

The ants are scavenging an abandoned ant hill in search of food.

The ant hill has nn chambers and n-1n−1 corridors connecting them.

We know that each chamber can be reached via a unique path from every other chamber.

In other words, the chambers and the corridors form a tree.

There is an entrance to the ant hill in every chamber with only one corridor leading into (or out of) it.

At each entry, there are gg groups of m_1,m_2,\cdots,m_gm​1​​,m​2​​,⋯,m​g​​ ants respectively.

These groups will enter the ant hill one after another, each successive group entering once there are no ants inside.

Inside the hill, the ants explore it in the following way:

• Upon entering a chamber with dd outgoing corridors yet unexplored by the group,the group divides into dd groups of equal size. Each newly created group follows one of the d corridors.If d=0d=0, then the group exits the ant hill.

• If the ants cannot divide into equal groups, then the stronger ants eat the weaker until a perfect division is possible.Note that such a division is always possible since eventually the number of ants drops down to zero.Nothing can stop the ants from allowing divisibility - in particular, an ant can eat itself, and the last one remaining will do so if the group is smaller than dd.

The following figure depicts mm ants upon entering a chamber with three outgoing unexplored corridors, dividing themselves into three (equal) groups of \left \lfloor m/3 \right \rfloor⌊m/3⌋ ants each.

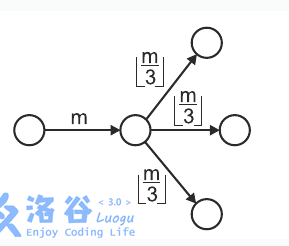
A hungry anteater dug into one of the corridors and can now eat all the ants passing through it.

However, just like the ants, the anteater is very picky when it comes to numbers.

It will devour a passing group if and only if it consists of exactly kk ants.

We want to know how many ants the anteater will eat.

给一棵树，对于每个叶子节点，都有g群蚂蚁要从外面进来，每群蚂蚁在行进过程中只要碰到岔路，就将平均地分成岔路口数-1那么多份，然后平均地走向剩下的那些岔路口，余下的蚂蚁自动消失，树上有一个关键边，假如有一群蚂蚁通过了这条边且数量恰好为k，这k只蚂蚁就被吃掉，问一共有多少只蚂蚁被吃掉

输入输出格式

输入格式：

The first line of the standard input contains three integers nn, gg, kk(2\le n,g\le 1\ 000\ 0002≤n,g≤1 000 000, 1\le k\le 10^91≤k≤10​9​​), separated by single spaces.

These specify the number of chambers, the number of ant groups and the number of ants the anteater devours at once. The chambers are numbered from 1 to nn.

The second line contains gg integers m_1,m_2,\cdots,m_gm​1​​,m​2​​,⋯,m​g​​ (1\le m_i\le 10^91≤m​i​​≤10​9​​), separated by single spaces, where m_im​i​​ gives the number of ants in the ii-th group at every entrance to the ant hill. The n-1n−1 lines that follow describe the corridors within the ant hill;the ii-th such line contains two integers a_ia​i​​,b_ib​i​​ (1\le a_i,b_i\le n1≤a​i​​,b​i​​≤n), separated by a single space, that indicate that the chambers no. a_ia​i​​ and b_ib​i​​ are linked by a corridor. The anteater has dug into the corridor that appears first on input.

输出格式：

Your program should print to the standard output a single line containing a single integer: the number of ants eaten by the anteater.

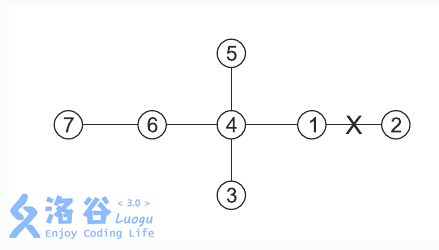
输入输出样例

输入样例#1：

7 5 3
3 4 1 9 11
1 2
1 4
4 3
4 5
4 6
6 7

输出样例#1：

21

说明

给一棵树，对于每个叶子节点，都有g群蚂蚁要从外面进来，每群蚂蚁在行进过程中只要碰到岔路，就将平均地分成岔路口数-1那么多份，然后平均地走向剩下的那些岔路口，余下的蚂蚁自动消失，树上有一个关键边，假如有一群蚂蚁通过了这条边且数量恰好为k，这k只蚂蚁就被吃掉，问一共有多少只蚂蚁被吃掉

树形dp

Ｏ(≧口≦)Ｏ做了一晚上、、、

我们会发现一个很严肃的问题，如果我们从子节点开始做的话会非常难处理（反正蒟蒻表示我不会、、、）

既然正着不会，我们就倒着搞吧、、其次他说的是通过一条边的数量为k，这k只蚂蚁都会被吃掉。然而我们如果直接用边来进行运算的话，既然这样我们直接将边改为这条边的两个节点，然后以这两个节点为根节点，将原来的树处理成两棵树。然后就可以在这两棵树上乱搞了

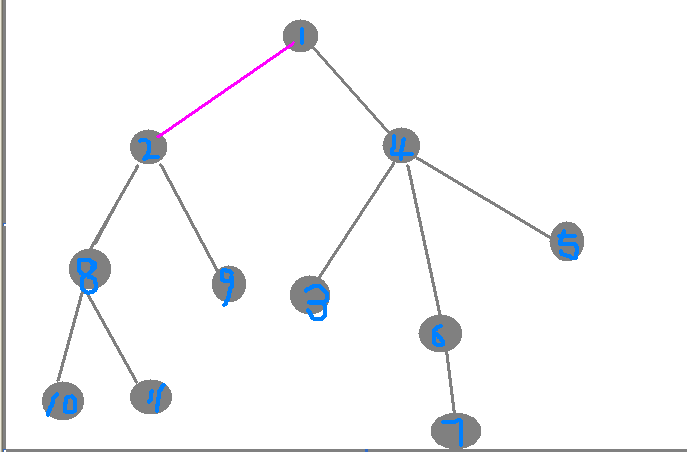如图所示：在1~2这条边上如果有k只蚂蚁经过的时候这k只蚂蚁会被吃掉

我们将上面的两棵树抽离成两颗一颗以1为根节点，一棵以2为根节点。

对于每一颗树我们从根节点开始往下进行搜索，更新每一个节点的父亲节点，如果这个点的父亲节点与他相连出去的节点不相同，那么将与他相连节点的父亲节点为当前节点。

我们看上面的图，如果要是蚂蚁经过1~2这条边上的时候蚂蚁的数量达到k时1号节点·与2好节点处的蚂蚁数量也就要为k。

然后我们在从这个各节点倒着计算他下面的节点蚂蚁的数量

我们知道进入蚂蚁的节点一定是子节点，然后每一个子节点往其他的分支那平分蚂蚁，他评分出来的蚂蚁一定是有一波要进入他的父亲节点。这样的话我们可以直接根据他的父亲节点的蚂蚁数目推出当前节点的蚂蚁数目，我们这个地方是不可能求出准确值的，因为他在平分的时候是下取整的。所以我们只能求出一个子节点的蚂蚁数目的范围。

子节点的蚂蚁的数目等于它的父节点的；连出去的边的条数*父节点的蚂蚁个数。

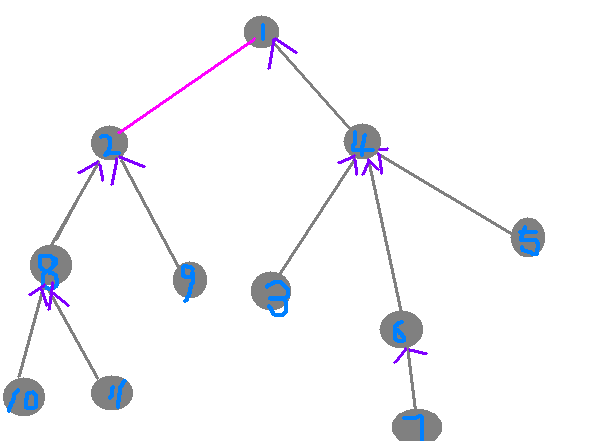看这个图，你可以发现一个规律它的父节点连出去的边的条数正好等于它的父节点的入读。我们可以在进行dfs的时候处理处每一个点的父亲节点以及该点的入读、

蚂蚁平分，子节点最少的蚂蚁的个数为他父亲节点的蚂蚁的数量*父亲节点的入读，也就是说没有蚂蚁被消灭。最多的蚂蚁的数量为还差一个蚂蚁就可以让每一个分支在多分一只蚂蚁了，极为maxn[t]=(sum[now]+1)*out[now]-1

然后dfs结束的条件的为他已经搜索到最后一层子节点了。当minn[to[i]]<=m[g]是说明还没有到达根节点。

然后我们可以处理处到达叶子节点的时候的蚂蚁的最多数量跟最少数量，然后在判断有多少组蚂蚁满足要求。

最后的可以吃到的蚂蚁的数量为k*满足条件的蚂蚁的组数

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 1100000
#define ll long long
using namespace std;
int n,g,k,x,y,sx,sy,tot;
int fa[N],in[N],head[N];
ll s[N],maxn[N],minn[N],ans;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
struct Edge
{
    int to,from,next;
}edge[N<<];
int add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].next=head[x];
    head[x]=tot;
}
int dfs(int now)
{
    for(int i=head[now];i;i=edge[i].next)
    {
        int t=edge[i].to;
        if(fa[now]!=t)
        {
            fa[t]=now;
            in[now]++;
         }
    }
    for(int i=head[now];i;i=edge[i].next)
    {
        int t=edge[i].to;
        if(fa[now]!=t)
        {
            minn[t]=minn[now]*in[now];
            maxn[t]=(maxn[now]+)*;
            maxn[t]=min(maxn[t],s[g]);
            if(minn[t]<=s[g]) dfs(t);
        }
    }
}
ll erfen(ll x)
{
    ,r=g,ans1=;
    while(l<=r)
    {
        ;
        if(s[mid]<x)
        {
            ans1=mid;
            l=mid+;
        }
        ;
    }
    return ans1;
}
int main()
{
    n=read(),g=read(),k=read();
    ;i<=g;i++) scanf("%lld",&s[i]);
    sort(s+,s++g);
    sx=read(),sy=read();
    ;i<n;i++)
    {
        x=read(),y=read();
        add(x,y),add(y,x);
    }
    minn[sx]=minn[sy]=maxn[sx]=maxn[sy]=k;
    dfs(sx),dfs(sy);
    ;i<=n;i++)
     if(!in[i])
      ans+=erfen(maxn[i]+)-erfen(minn[i]);
    printf("%lld",ans*k);
    ;
}