BZOJ 4815 数论

今年的重庆省选？

具体就是，对于每次修改，A[p,q]这个位置，  设d=gcd(p,q) ,则 gcd为d的每一个格子都会被修改，且他们之间有个不变的联系

A[p,q]/p/q==A[k,t]/k/t   所以只要记录对于gcd为d的所有格子，只要保存A[d][d]的值就可以了。

那么求前k行k列的值ans，则所有gcd(p,q)==d的A[p,q]对答案的贡献就是    {

　　　　　　设k'=k/d;  （下取整）  f[k']*A[p,q]/(p/d)/(q/d)

}

首先有个基本结论（当n>1时）：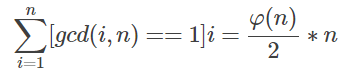

（ 若x与n互质，则n-x也与n互质 →  与n互质的数的平均数是n/2）

然后推得   f[n]=

代码如下：【BZOJ里最短了吧。。跑的也挺快】

 #include <bits/stdc++.h>
 #define LL long long
 using namespace std;
 const LL mo=;
 int S,n,m,k,t,p,q,a[],f[],op[][];
 LL d,x,ans;
 int gcd(int x,int y){ return y?gcd(y,x%y):x;}
 int main(){
     scanf("%d%d",&m,&n); f[]=;
     for (int i=;i<=n;++i){
         if (!a[i]) a[++t]=i,f[i]=i-;
         for (int j=;j<=t;++j){
             x=a[j]*i; if (x>n) break; a[x]=;
             if (!(i%a[j])) {f[x]=f[i]*a[j]; break; }else f[x]=f[i]*f[a[j]];
         }
     }
     for (int i=;i<=n;++i) f[i]=((LL)i*i%mo*f[i]+f[i-])%mo;
     for (int i=;i<=m;++i){
         scanf("%d%d%lld%d",&p,&q,&x,&k);
         d=gcd(p,q); p/=d; q/=d;
         op[i][]=d; op[i][]=(x/p/q-d*d)%mo;
         if (op[i][]<) op[i][]+=mo;
         ans=(LL)(+k)*k/%mo;
         ans=ans*ans%mo;
         for (int j=;j<=i;++j)
         if (op[j][]){
             if (j!=i&&op[j][]==d){ op[j][]=; continue;}
             ans+=(LL)f[k/op[j][]]*op[j][]%mo;
             if (ans>=mo) ans-=mo;
         }
         printf("%lld\n",ans);
     }
     return ;
 }

杀老师

然后附 查了一个下午的 智障错误。。

看第21行。x/p/q-d*d， 原来这个d是不开LL的。然而 d*d可能会爆int 所以，以前一直下意识的以为只要表达式把(LL)x放最前面 后面就会自动转成LL了 。现在看来是要留个心眼了。。