HDU 2845 Beans (两次线性dp)

Beans

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 3521    Accepted Submission(s): 1681

Problem Description

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect
the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.

Now, how much qualities can you eat and then get ?

 

Input

There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that
the quality of bean isn't beyond 1000, and 1<=M*N<=200000.

 

Output

For each case, you just output the MAX qualities you can eat and then get.

 

Sample Input

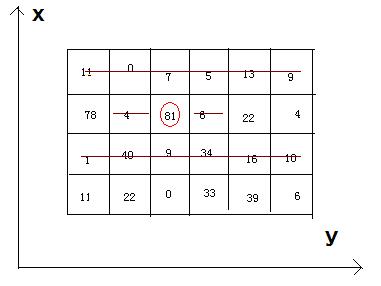
4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6

 

Sample Output

242

 

Source

2009 Multi-University Training Contest 4 -
Host by HDU



题目链接：

pid=2845">http://acm.hdu.edu.cn/showproblem.php?

pid=2845



题目大意：在一个矩阵中选择一些数，要求和最大，假设选择(x,y)位置的数。则(x, y+1)，(x,y-1)位置不可选。第x+1和第x-1行都不可选



题目分析：题目给了m*n的范围，就是不让你开二维开开心心切掉。只是不影响。一维照样做。先对于每一行dp一下，求出当前行能取得的最大值

tmp[j] = max(tmp[j - 1]，a[i + j - 1] + tmp[j - 2])第一个表示不选第i行第j列得数字。第二个表示选，取最大，则最后tmp[m]为当前行最大的

然后由于相邻两行不能同一时候取，我再对行做一次dp

 dp[i] = max(dp[i - 1], dp[i - 2] + row[i])，第一个表示不选第i行，第二个表示选第i行，取最大，则最后dp[cnt - 1]即为答案

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int const MAX = 2 * 1e5 + 5;
int row[MAX], a[MAX], dp[MAX], tmp[MAX];

int main()
{
    int n, m;
    while(scanf("%d %d", &n, &m) != EOF)
    {
        memset(tmp, 0, sizeof(tmp));
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= m * n; i++)
            scanf("%d", &a[i]);
        int cnt = 1;
        for(int i = 1; i <= m * n; i += m)
        {
            for(int j = 2; j <= m; j++)
            {
                tmp[1] = a[i];
                tmp[j] = max(tmp[j - 1], a[i + j - 1] + tmp[j - 2]);
            }
            row[cnt ++] = tmp[m];
        }
        dp[1] = row[1];
        for(int i = 2; i < cnt; i++)
            dp[i] = max(dp[i - 1], dp[i - 2] + row[i]);
        printf("%d\n", dp[cnt - 1]);
    }
}