POJ 2117 Electricity（割点求连通分量）

http://poj.org/problem?id=2117

题意：
求删除图中任意一个顶点后的最大连通分量数。

思路：

求出每个割点对应的连通分量数，注意这道题目中图可能是不连通的。

这道题目我wa了很多发，主要是我忘了根结点的连通分量数得减1。

为什么呢？因为如果我们用cut[]来记录每个结点对应的连通分量数的话，最后的答案还需要加1。

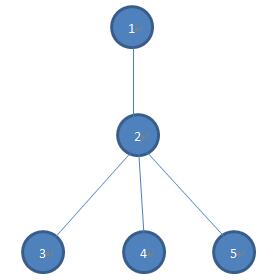
比如2结点，我们计算所得的cut[2]=3，因为它只计算了它的子树的情况，但是父亲结点并没有计算进去，所以最后需要+1，这个1也就是父亲结点方向也会产生一个连通分量，这是肯定的，因为父亲结点方向就这么一条边。那根结点是没有父亲结点的，所以根结点需要-1。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,ll> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;
 
 int n, m;
 int tot;
 int sum;
 int ans;
 int dfs_clock;
 int iscut[maxn];
 int pre[maxn];
 int head[maxn];
 
 struct node
 {
     int v;
     int next;
 }e[*maxn];
 
 void addEdge(int u, int v)
 {
     e[tot].v=v;
     e[tot].next=head[u];
     head[u]=tot++;
 }
 
 int dfs(int u, int fa)
 {
     int lowu=pre[u]=++dfs_clock;
     int child=;
     for(int i=head[u];i!=-;i=e[i].next)
     {
         int v=e[i].v;
         if(!pre[v])
         {
             child++;
             int lowv=dfs(v,u);
             lowu=min(lowu,lowv);
             if(lowv>=pre[u])   iscut[u]++;
         }
         else if(pre[v]<pre[u] && v!=fa)
         {
             lowu=min(lowu,pre[v]);
         }
     }
     if(fa< && child>=)   iscut[u]--;  //这儿很重要，根结点必须-1
     return lowu;
 }
 
 void solve()
 {
     sum=;
     ans=;
     memset(pre,,sizeof(pre));
     memset(iscut,,sizeof(iscut));
     for(int i=;i<n;i++)
     {
         if(!pre[i])
         {
             sum++;
             dfs_clock=;
             dfs(i,-);
         }
         ans=max(ans,iscut[i]);
     }
 }
 
 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n,&m))
     {
         if(n== && m==)  break;
         if(m==)  {printf("%d\n",n-);continue;}
         tot=;
         memset(head,-,sizeof(head));
         while(m--)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             addEdge(u,v);
             addEdge(v,u);
         }
         solve();
         printf("%d\n",sum+ans);
     }
     return ;
 }