python数据结构之树（二叉树的遍历）

树是数据结构中非常重要的一种，主要的用途是用来提高查找效率，对于要重复查找的情况效果更佳，如二叉排序树、FP-树。

本篇学习笔记来自：二叉树及其七种遍历方式、python遍历与非遍历方式实现二叉树

介绍：

树的遍历主要有两种，一种是深度优先遍历，像前序、中序、后序；另一种是广度优先遍历，像层次遍历。

在树结构中两者的区别还不是非常明显，但从树扩展到有向图，到无向图的时候，深度优先搜索和广度优先搜索的效率和作用还是有很大不同的。

深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。

以下面树图为例写代码实现：

'''
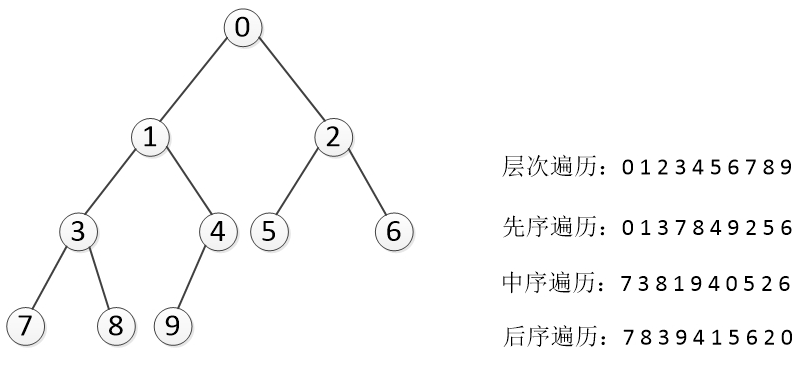
树的构造
1.递归实现先序遍历、中序遍历、后序遍历
2.堆栈实现先序遍历、中序遍历、后序遍历
3.队列实现层次遍历
'''
#节点类
class Node(object):
    __slots__ = 'item','lchild','rchild'

    def __init__(self,item=None,lchild=None,rchild=None):
        self.item = item
        self.lchild = lchild
        self.rchild = rchild

#树类
class Tree(object):
    def __init__(self):
        self.root = root
        self.myQueue = myQueue

    #添加树节点
    def add(self,item):
        node = Node(item)
        if self.root.item == None:  #空则赋值root
            self.root = node
            self.myQueue.append(self.root)
        else:
            treeNode = self.myQueue[0]  #该节点子树还没齐
            if treeNode.lchild == None:
                treeNode.lchild = node
                self.myQueue.append(treeNode.lchild)
            else:
                treeNode.rchild = node
                self.myQueue.append(treeNode.rchild)
                self.myQueue.pop(0)   #如果该节点在右子树，丢弃该节点

    #递归实现树的先序遍历
    def front_digui(self,root):
        if root == None:
            return None
        print(root.item)
        self.front_digui(root.lchild)
        self.front_digui(root.rchild)

    #递归实现树的中序遍历
    def middle_digui(self,root):
        if root == None:
            return None
        self.middle_digui(root.lchild)
        print(root.item)
        self.middle_digui(root.rchild)

    #递归实现树的后序遍历
    def later_digui(self,root):
        if root == None:
            return None
        self.later_digui(root.lchild)
        self.later_digui(root.rchild)
        print(root.item)

    #利用堆栈实现树的先序遍历
    def front_stack(self, root):
        if root == None:
            return
        myStack = []
        node = root
        while node or myStack:
            while node:    #从根节点开始，一直找它的左子树
                print（node.item）
                myStack.append(node)
                node = node.lchild
            node = myStack.pop()    #while结束表示当前节点node为空，即前一个节点没有左子树了
            node = node.rchild      #开始查看它的右子树

    #利用堆栈实现树的中序遍历
    def middle_stack(self, root):

        if root == None:
            return
        myStack = []
        node = root
        while node or myStack:
            while node:              #从根节点开始，一直找它的左子树
                myStack.append(node)
                node = node.lchild
            node = myStack.pop()        #while结束表示当前节点node为空，即前一个节点没有左子树了
            print node.item,
            node = node.rchild            #开始查看它的右子树

    #利用堆栈实现树的后序遍历
    def later_stack(self, root):

        if root == None:
            return
        myStack1 = []
        myStack2 = []
        node = root
        myStack1.append(node)
        while myStack1:               #这个while循环的功能是找出后序遍历的逆序，存在myStack2里面
            node = myStack1.pop()
            if node.lchild:
                myStack1.append(node.lchild)
            if node.rchild:
                myStack1.append(node.rchild)
            myStack2.append(node)
        while myStack2:                  #将myStack2中的元素出栈，即为后序遍历次序
            print(myStack2.pop().item)

    #利用队列实现树的层次遍历
    def level_queue(self, root):

        if root == None:
            return
        myQueue = []
        node = root
        myQueue.append(node)
        while myQueue:
            node = myQueue.pop(0)
            print node.item,
            if node.lchild != None:
                myQueue.append(node.lchild)
            if node.rchild != None:
                myQueue.append(node.rchild)

#测试
if __name__ == '__main__':
    items = range(10)           #生成十个数据作为树节点
    tree = Tree()          #新建一个树对象
    for item in items:
        tree.add(item)           #逐个添加树的节点

    print('队列实现层次遍历:')
    tree.level_queue(tree.root)

    print('\n\n递归实现先序遍历:')
    tree.front_digui(tree.root)
    print('\n递归实现中序遍历:')
    tree.middle_digui(tree.root)
    print('\n递归实现后序遍历:')
    tree.later_digui(tree.root)

    print('\n\n堆栈实现先序遍历:')
    tree.front_stack(tree.root)
    print('\n堆栈实现中序遍历:')
    tree.middle_stack(tree.root)
    print('\n堆栈实现后序遍历:')
    tree.later_stack(tree.root)

#输出结果

队列实现层次遍历:
0
1
2
3
4
5
6
7
8
9

递归实现先序遍历:
0
1
3
7
8
4
9
2
5
6

递归实现中序遍历:
7
3
8
1
9
4
0
5
2
6

递归实现后序遍历:
7
8
3
9
4
1
5
6
2
0

堆栈实现先序遍历:
0
1
3
7
8
4
9
2
5
6

堆栈实现中序遍历:
7
3
8
1
9
4
0
5
2
6

堆栈实现后序遍历:
7
8
3
9
4
1
5
6
2