WebGL编程指南高级技术篇（常见需求的处理）

一、鼠标控制模型旋转

实质的根据鼠标移动前后的位置比较得出x，y轴的旋转角度；

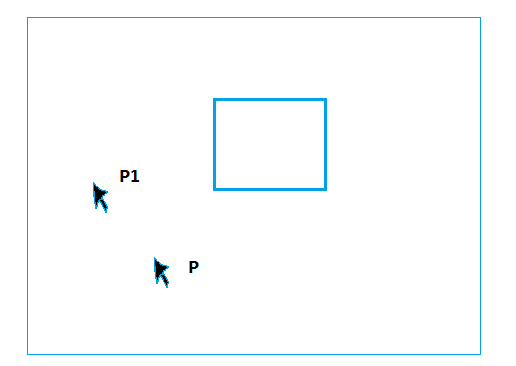
图中是一个屏幕，有一个模型（恩，他是一个模型），鼠标由P点移动到P1点，我们假定移动单位步长旋转β角度；

P（x1,y1）--->P1（x2,y2），x轴移动（x2-x1），y轴移动（y2-y1），所以x轴旋转 （x2-x1）β度，y轴旋转（y2-y1）β度：

二、判断物体被点击

当鼠标点击的时候，将物体颜色全置为红色，然后取鼠标点击坐标点的颜色，然后将物体颜色还原，再将之前获取的坐标点颜色做判断：

如果颜色为红色，那么就说明，点击到了物体。

点完之后，要将顶点着色器内判断是否点击的变量重置为false，从而使得重绘为正常颜色。

三、判断面被点击

前面我们知道，绘制面的时候，是通过告知这个面包含那几个顶点来进行绘制的：

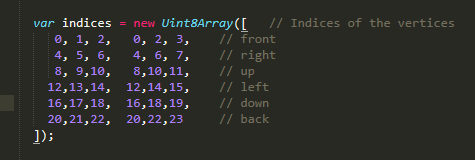
二在这里，为了实现判断面的点击，我们加入了面的序号这个概念，

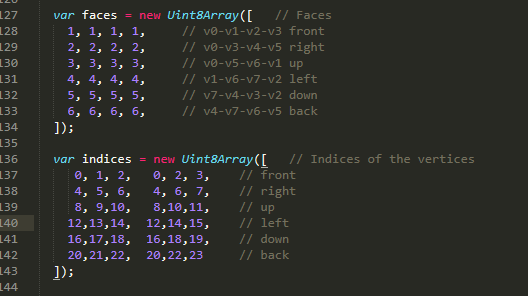
这样一来，每个顶点除了坐标、颜色，发向量之外，多了一个面序号的属性。当我们点击的时候：

直接就获取了点击位置的面编号，兵器将其传递给顶点着色器，进行判断并绘制：

四、HUD平视显示器/网页上方显示3D物体

就是在三维canvas（z-index = 1）上覆盖一个canvas（z-index = 2），用来显示2D信息（实时显示一些提示性消息），前置canvas的背景色为透明。

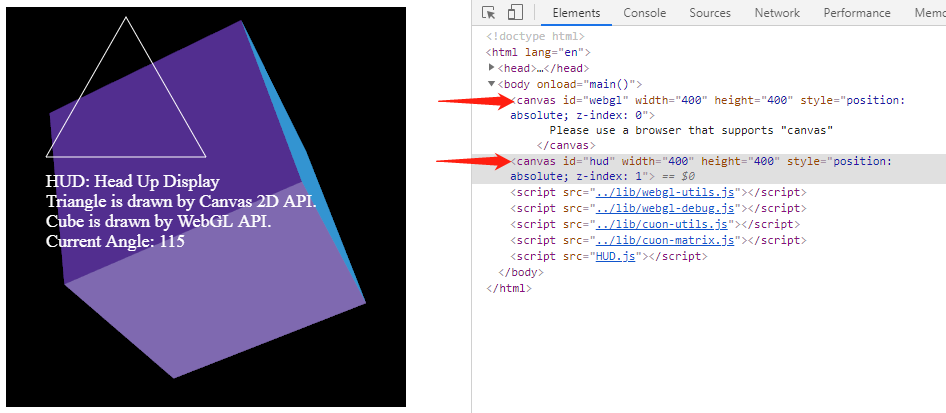
鼠标点击事件注册到2D的canvas上，因为两个canvas是重叠的，所以点击2D上的点，就相当于点击了WebGL上的点了。

后续该怎么绘制怎么绘制：

对于网页上方显示3D，道理相同，将3D的canvas，绝对定位在html上，或者指定节点位置，背景色透明。

五、雾化效果

六、绘制圆点

主要是在片元着色器中使用gl_PointCoord变量

七、α混合实现透明