Multi-target tracking by Lagrangian relaxation to min-cost network flow
Multi-target tracking by Lagrangian relaxation to min-cost network flow
读 “Multi-target tracking by lagrangian relaxation to min-cost network flow, CVPR,2013”小结。
昨晚老板让看一下这篇文章写几句总结给他,所以就看了看,今天顺便简单总结一下这篇文章。
这篇文章模型的核心依然是网络流算法,但和一般网络流算法不同点在于:一般方法在构建图时直接将每一个observation作为node,而observation之间的相互关系使用edge表示,这样每个edge表示的时相连node之间的相似度或者关联程度;而这篇文章所提模型中,在构建图时使用的是candidate pair作为node,然后pair of candidate pairs之间存在这edge,通过这种方式,能够将连续三帧之间的高阶信息,比如连续三帧之间速度近似恒定,融入到模型中。而正是由于不同的构图方式,导致必须引入一些附加的约束以满足多目标跟踪中 track-detection之间的一对一关系。对于提出的模型,通过适当的拉格朗日松弛可以转化为一般的网络流算法有效求解。
illustrative overview of proposed graph representation
使用一个简单的例子清楚的阐述了模型的构图方式。
假设现在有连续的三帧图像的observations。第一帧有3个表示为1,2,3,第二帧有两个表示为4,5,第三帧3个表示为6,7,8.一般网络流算法的构图方式如下(这里没有添加源点和汇点)
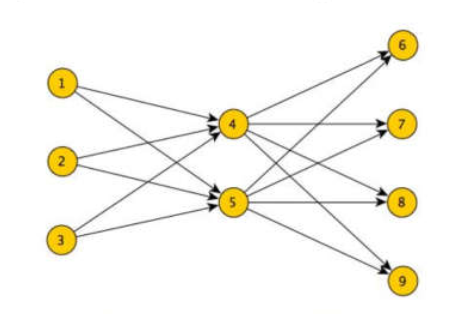
每条edge的流量是一个二值变量 , 网络流显然应该满足流量守恒约束,每条edge上的代价即相连两个不同帧间observations的匹配程度,然后可以使用最小费用流算法求解模型。
, 网络流显然应该满足流量守恒约束,每条edge上的代价即相连两个不同帧间observations的匹配程度,然后可以使用最小费用流算法求解模型。
上面模型中每条edge上的代价仅仅描述了两帧的相连observations之间的匹配程度,而MTT问题中更高阶的信息往往更加有用。于是作者提出了下面这种构图方式
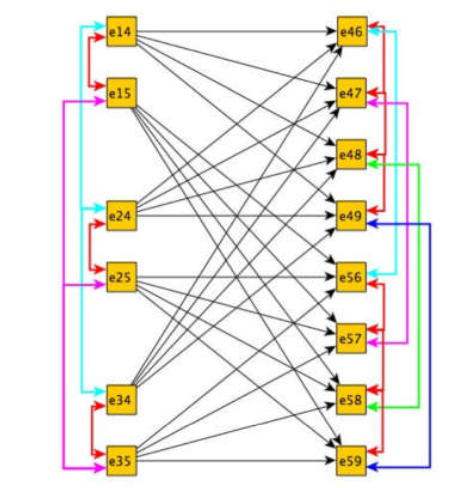
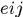 表示observations i 和j之间的连接关系,比如
表示observations i 和j之间的连接关系,比如 表示observations 1和4之间的连接关系。将连续两帧之间可能存在的匹配作为nodes,比如1,2两帧和2,3两帧的可能匹配都抽象为nodes,然后不同帧间的匹配如果存在公共点,则两个匹配之间存在edge,比如1,2两帧之间的匹配
表示observations 1和4之间的连接关系。将连续两帧之间可能存在的匹配作为nodes,比如1,2两帧和2,3两帧的可能匹配都抽象为nodes,然后不同帧间的匹配如果存在公共点,则两个匹配之间存在edge,比如1,2两帧之间的匹配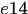 和2,3帧之间的匹配
和2,3帧之间的匹配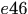 之间就存在edge。这样每个edge的cost就是两个匹配之间的相似度,匹配的信息可以包括连接的observations的相对速度和表观差异,这样edge的cost就可以包含相连三帧之间的observations的高阶信息。
之间就存在edge。这样每个edge的cost就是两个匹配之间的相似度,匹配的信息可以包括连接的observations的相对速度和表观差异,这样edge的cost就可以包含相连三帧之间的observations的高阶信息。
MTT中一般假设(当然现在好多方法去掉了这个约束):一条轨迹在任一帧中只能匹配一个observation,同样一个observation只能对应一条轨迹。所以提出的模型中就要对nodes添加额外约束以解决nodes之间的耦合关系,即上图中彩色连线连接的nodes,只能多选一,比如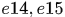 ,由于两个都经过observation 1,为了满足一一对应约束,必须只能二选一。
,由于两个都经过observation 1,为了满足一一对应约束,必须只能二选一。
problem formulation
形式化表述模型。
现有长度为 的图像序列,第
的图像序列,第 帧中有
帧中有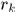 个observations,其集合表示为
个observations,其集合表示为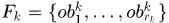 ,
, 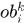 表示第k帧的第i个目标。
表示第k帧的第i个目标。
相邻帧之间可能的匹配对是一个二元组,表示为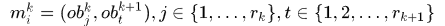 ,这些可能的匹配可以由表观相似度,距离相似度等获得。 帧k与k+1之间所有可能的匹配个数表示为
,这些可能的匹配可以由表观相似度,距离相似度等获得。 帧k与k+1之间所有可能的匹配个数表示为 ,其集合表示为
,其集合表示为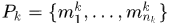 。 那么整个序列中nodes个数为
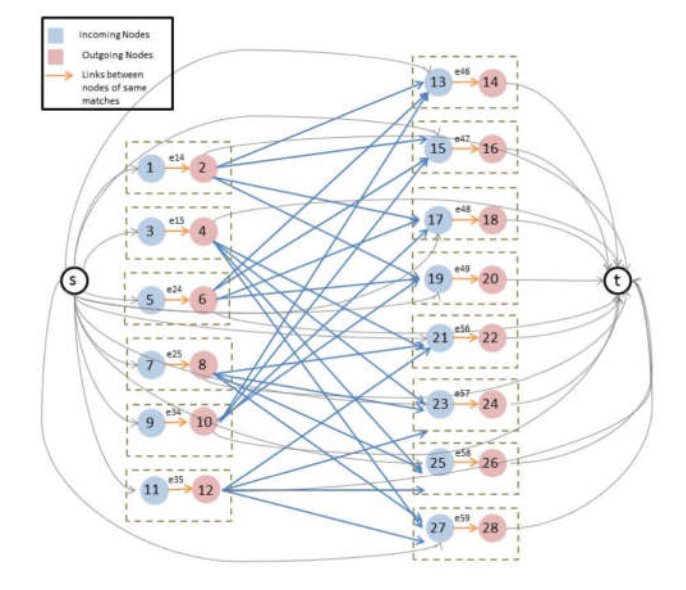
。 那么整个序列中nodes个数为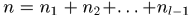 ,其总的集合表示为
,其总的集合表示为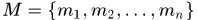 .
.
由图2进一步细化的图如下:G=(V,E),其中V包含源点s和汇点t,以及每一个match链接的两个observations,称为incoming node和outgoing node。 .
.
将每个match表示成两个nodes有两个好处:
1.由于每条边的流量最大为1和流量平衡约束,那么离开outgoing点的流量最多只能为1,因为只有一条进入的link
2.这么做可以将一般网络流算法中unary和binary约束直接添加到match内部的link上,而高阶信息都放在了match与match之间deges上了。
注意这里一直在说连续3帧图像,起始强调3帧只是为了融合高阶信息。像遮挡这种问题就不一定非要是连续帧,通过非连续帧构造类似的图一样可以求解。
整个模型表示如下
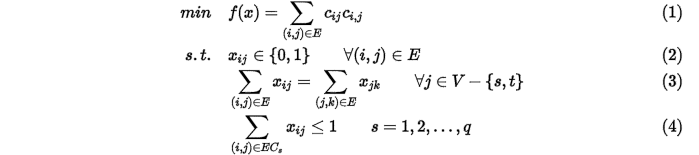
其中 表示边ij的代价,(1)表示最小代价,(2)表示二值约束,(3)表示流量平衡约束,(4)表示附加的用于一一对应的约束。(1)(2)(3)就是一般的网络流算法模型,针对于约束(4),
表示边ij的代价,(1)表示最小代价,(2)表示二值约束,(3)表示流量平衡约束,(4)表示附加的用于一一对应的约束。(1)(2)(3)就是一般的网络流算法模型,针对于约束(4), 表示第s个由outgoing和incoming点重合的matches构成的集合,整个序列总共有q个这种集合。
表示第s个由outgoing和incoming点重合的matches构成的集合,整个序列总共有q个这种集合。
为了求解该模型,将约束(4)通过拉格朗日松弛放到目标式中,然后就可以转换为一般的网络流算法模型进行求解。

其中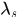 表示拉格朗日乘子
表示拉格朗日乘子
stopping criteria
因为一些约束可能本身过强,始终不可能满足,所以迭代过程可能一直不收敛,这是采用限制最大迭代次数的方式终止算法。
对迭代得到的结果进一步后处理:
连接选中的matches组成tracks
将存在冲突的track拎出来放到一个“competing tracks”的list中
在conflicted tracks中选择lowest cost的track作为正确的track取出
针对于conflicted tracks剩下的tracks,剔除冲突的match看其是否依然能够满足轨迹的条件,比如前后光滑,长度等,满足则创建新的轨迹,不满足就扔掉。
Experiments
文中分别在psu,TUD和ETHMS数据库上进行了实验,具体实验结果参见论文。
conclusion
1.该模型相对于一般的网络流算法使用了更高阶的信息
2.但这里的更高阶也仅仅是3阶的信息,现在有一些利用更高阶信息的方法提出,比基于如张量秩一近似的多目标跟踪。
3.模型通过拉格朗日松弛可以有效的转化为一般的网络流算法求解。
4.针对于算法不收敛的情形,采用了一种贪婪算法作为强制算法结束的补
Multi-target tracking by Lagrangian relaxation to min-cost network flow的更多相关文章
- min cost max flow算法示例
问题描述 给定g个group,n个id,n<=g.我们将为每个group分配一个id(各个group的id不同).但是每个group分配id需要付出不同的代价cost,需要求解最优的id分配方案 ...
- LeetCode算法题-Min Cost Climbing Stairs(Java实现)
这是悦乐书的第307次更新,第327篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第176题(顺位题号是746).在楼梯上,第i步有一些非负成本成本[i]分配(0索引). ...
- [Swift]LeetCode746. 使用最小花费爬楼梯 | Min Cost Climbing Stairs
On a staircase, the i-th step has some non-negative cost cost[i] assigned (0 indexed). Once you pay ...
- Geeks面试题:Min Cost Path
Min Cost Path Given a cost matrix cost[][] and a position (m, n) in cost[][], write a function tha ...
- Min Cost Climbing Stairs - LeetCode
目录 题目链接 注意点 解法 小结 题目链接 Min Cost Climbing Stairs - LeetCode 注意点 注意边界条件 解法 解法一:这道题也是一道dp题.dp[i]表示爬到第i层 ...
- Leetcode 746. Min Cost Climbing Stairs 最小成本爬楼梯 (动态规划)
题目翻译 有一个楼梯,第i阶用cost[i](非负)表示成本.现在你需要支付这些成本,可以一次走两阶也可以走一阶. 问从地面或者第一阶出发,怎么走成本最小. 测试样例 Input: cost = [1 ...
- 746. Min Cost Climbing Stairs@python
On a staircase, the i-th step has some non-negative cost cost[i] assigned (0 indexed). Once you pay ...
- LN : leetcode 746 Min Cost Climbing Stairs
lc 746 Min Cost Climbing Stairs 746 Min Cost Climbing Stairs On a staircase, the i-th step has some ...
- LeetCode 746. 使用最小花费爬楼梯(Min Cost Climbing Stairs) 11
746. 使用最小花费爬楼梯 746. Min Cost Climbing Stairs 题目描述 数组的每个索引做为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i].(索引从 0 ...
随机推荐
- linux 图形界面的安装
本文内容主要摘自:http://blog.csdn.net/hotday_kevin/article/details/8310054 文中图形的安装和卸载都给了两种方式,貌似是因为都是版本的问题而不同 ...
- [转载]ViewState使用小结
ViewState是.Net中提出的状态保存的一种新途径,web程序保存状态的方式有这样几种:1.Application:保存在Application中的数据是全局有效的:Application里面存 ...
- web前端----html基础
一.初始html 1.web服务本质 import socket sock=socket.socket(socket.AF_INET,socket.SOCK_STREAM) sock.bind((&q ...
- Spring Boot 踩坑之路之 Configuration Annotation Proessor not found in classpath
1. 出现spring boot Configuration Annotation Proessor not found in classpath的提示是在用了@ConfigurationProper ...
- Python 技术点
1.文件操作 1-1 遍历文件夹和文件 import os rootDir = "/path/to/root" for parent, dirnames, filenames in ...
- 20145104张家明 《Java程序设计》第7周学习总结
20145104张家明 <Java程序设计>第7周学习总结 教材学习内容总结 第13章 简单认识时间和日期 -时间的度量:GMT.UT.TAI.UTC.Unix.epoch. -UTC:保 ...
- Python3基础 函数 未指定返回值,返回NONE
Python : 3.7.0 OS : Ubuntu 18.04.1 LTS IDE : PyCharm 2018.2.4 Conda ...
- Linux虚拟内存和物理地址的理解【转】
本文转载自:http://blog.csdn.net/dlutbrucezhang/article/details/9058583 在多任务操作系统中的每一个进程都运行在一个属于它自己的内存沙盘中.这 ...
- 51NOD 1066 Bash游戏
1066 Bash游戏 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 有一堆石子共有N个.A B两个人轮流拿,A先拿.每次最少拿1颗,最多拿K颗,拿到最后1颗石子的 ...
- [JavaScript] - form表单转json的插件
jquery.serializejson.js 之前好像记录过,做项目又用到了再记下 在页面中引入js后就可以使用了 示例: //点击设置微信信息的form表单提交按钮后,执行wxConfig的con ...
