github之无命令可视化界面操作——GitHub DeskTop

　　Git是Linuxs之父Lunus用C语言写的一个非常好用的分布式版本控制系统。

　　GitHub可以给我们提供免费的代码仓库，并用Git可以在上面提交代码并进行版本控制。使用Git一般要安装Git ，并用Git命令进行相关操作，每次修改都要add——commit——push。如果不想使用纯命令的操作可以下载GitHub DeskTop桌面软件，进行无命令的可视化界面操作。

      这里介绍一下GitHub DeskTop的基本操作及需要注意的地方。

 

　　下载并安装GitHub DeskTop （下载链接https://desktop.github.com）。

　

　　安装之后会有一个 GitHub桌面软件和一个Git Shell终端。

　    　　　　　

　　Git Shell的用法和Git Bash 差不多，这里着重介绍GitHub桌面软件。

　　打开用你的GiHub DeskTop并用GitHub帐号密码登录。现在是里面内容是空的，需要手动新建本地仓库或者，导入已有本地仓库，再或者从远程克隆仓库。登陆后的界面如下

　　会看到有个"+"按钮。

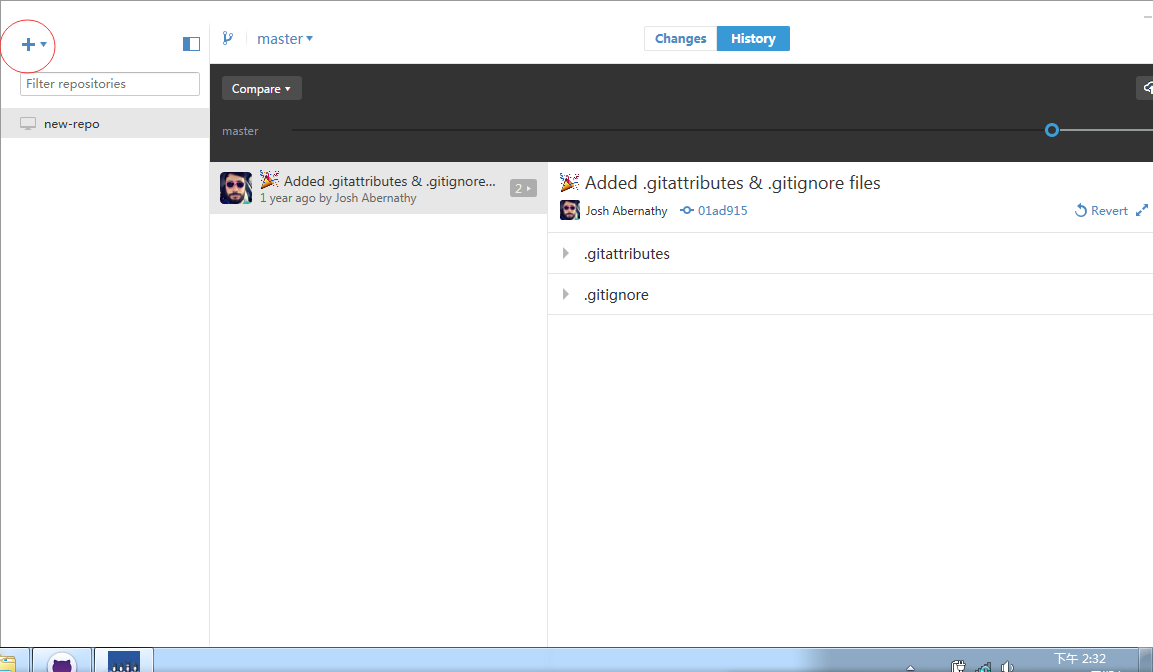
　　"+"和GitHub网页上的功能差不多。不过GitHub上的是创建远程版本库，这里的"+"是针对与本地版本库的。可以添加（导入）本地已有版本库，创建本地版本库，clone远程版本库。点击"+"按钮可以看到对应三个功能的三个选项分别是：add create clone。

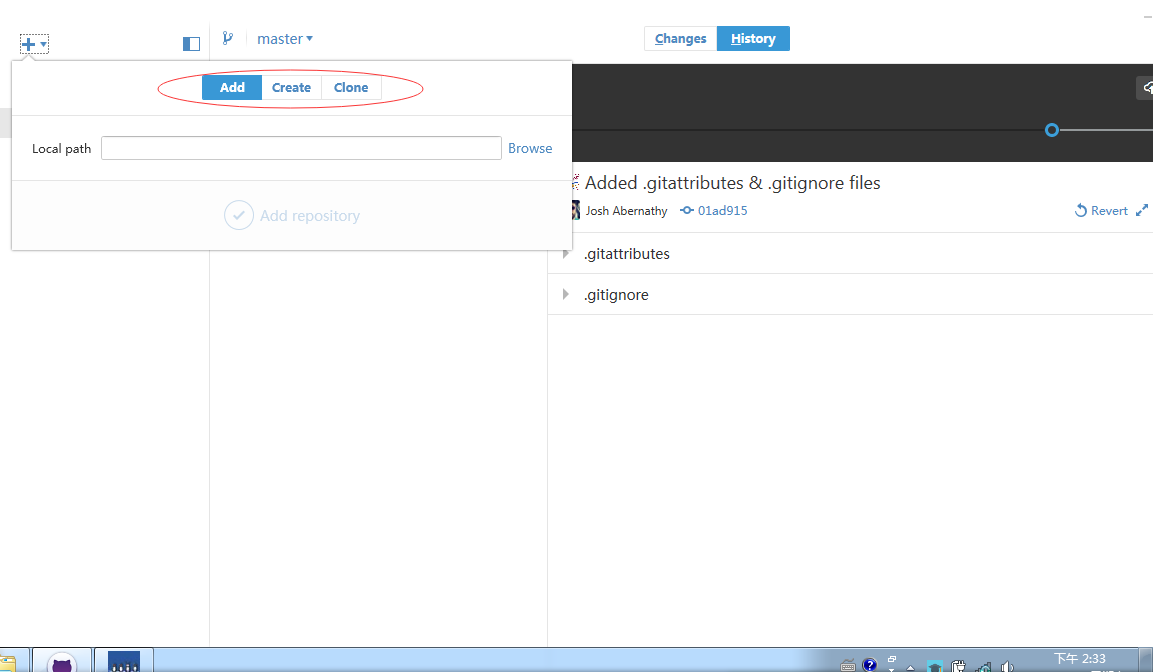
　　1.add——添加本地版本库

　　（这里添加DaisyWang88.github.io最好是通过GitHub DeskTop创建的版本库，而不是本地远程分开创建Git Bash连接的版本库，否则commit会失败）

　　添加之后会发现界面不再为空，在"History"下显示了当前版本库相关的历史信息。

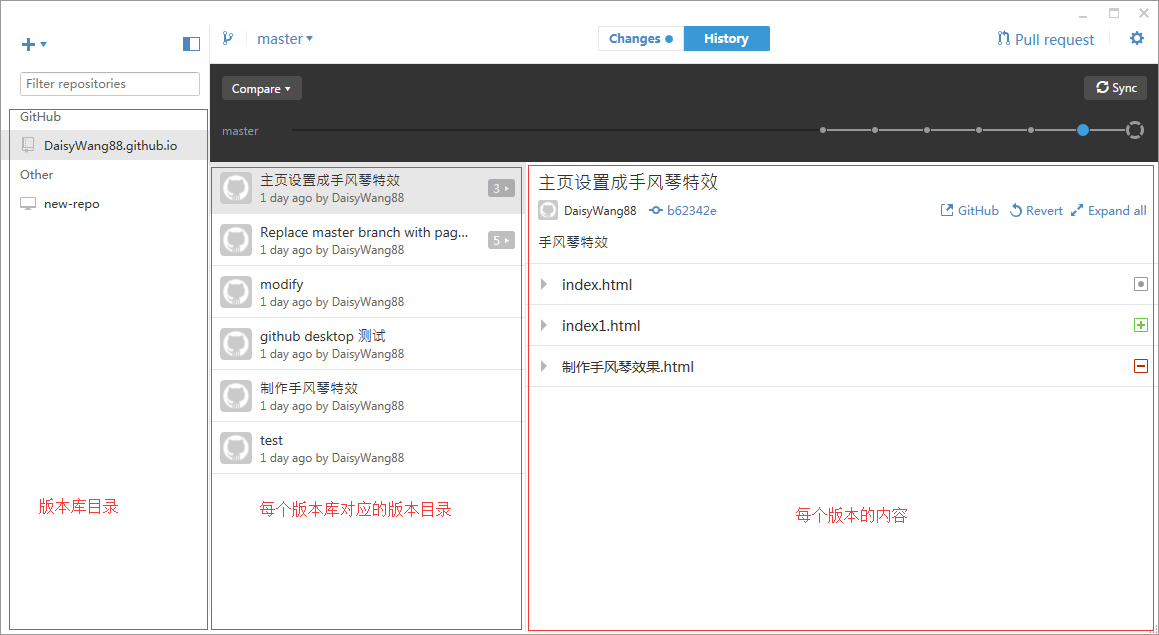
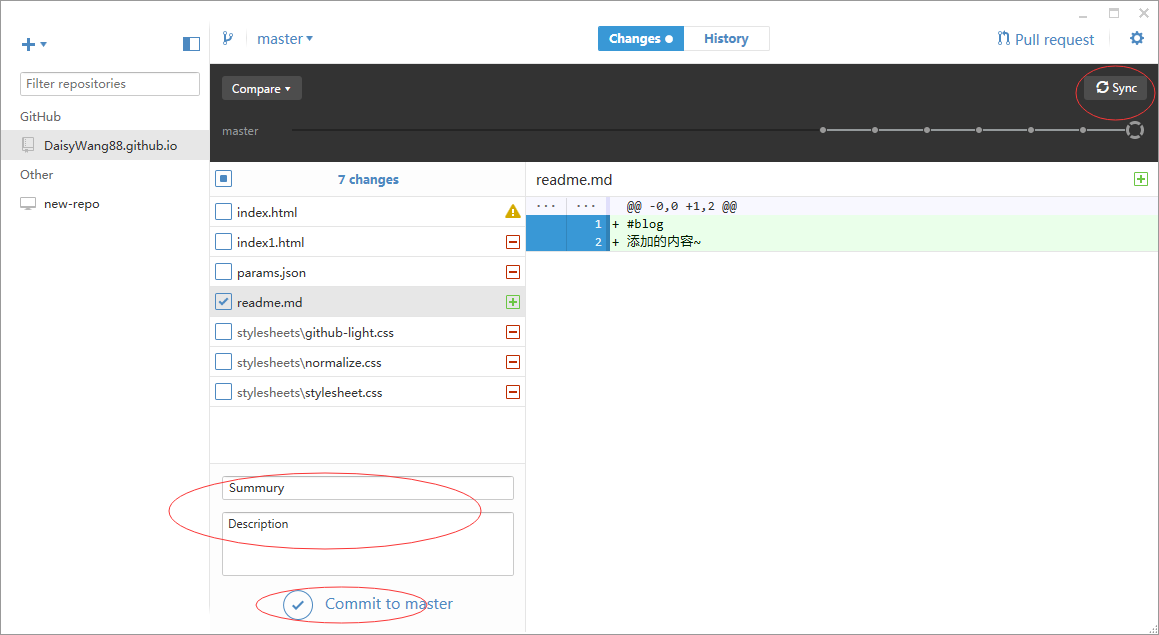
　　现在在本地的DaisyWang88.github.io中的文件进行修改，在"Changes选项下"立马可以看到有所变动的文件目录和内容。文件标题后面有+ 表示文件是新建的，- 表示文件被删除了，！表示文件存在冲突。

　　可以对有所变动的文件勾选，然后commit——Sycn至此修改就提交到远程的GitHub上去了，可以在GitHub网页上看到修改内容。

2.create——创建本地版本库

　　如下，路径是包含路径，下图是指在e:\\gitHub\路径下建一个名为test的本地仓库。

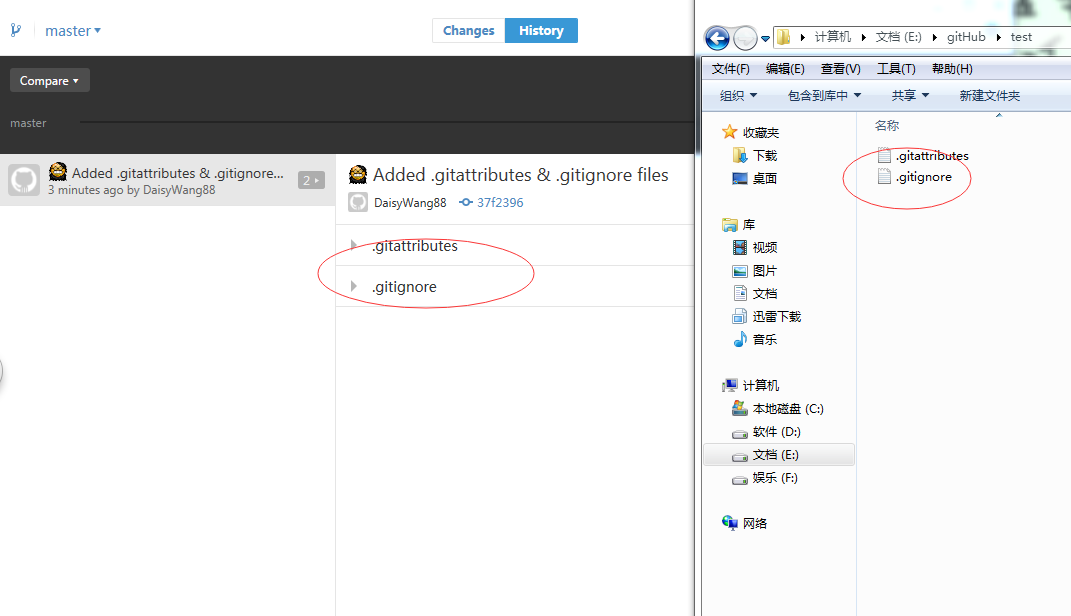
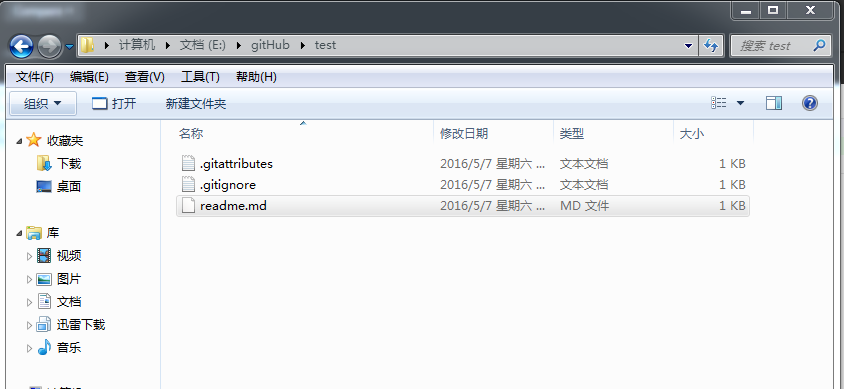
　　  此时打开本地的test文件会发现默认有两个文件 .gitattributes 和.gitignore两个文件，create本地仓库的时候就默认有这两个文件。

  　　此时在test文件里面添加一个readme.md文件写入“##这是一个测试文件”，如图点击蓝色的“Changes”按钮会同步显示，你在本地test文件当中做的修改，左边是修改的文件（我这里是添加了一个readme.md文件），右边同步显示文件修改之后的内容。

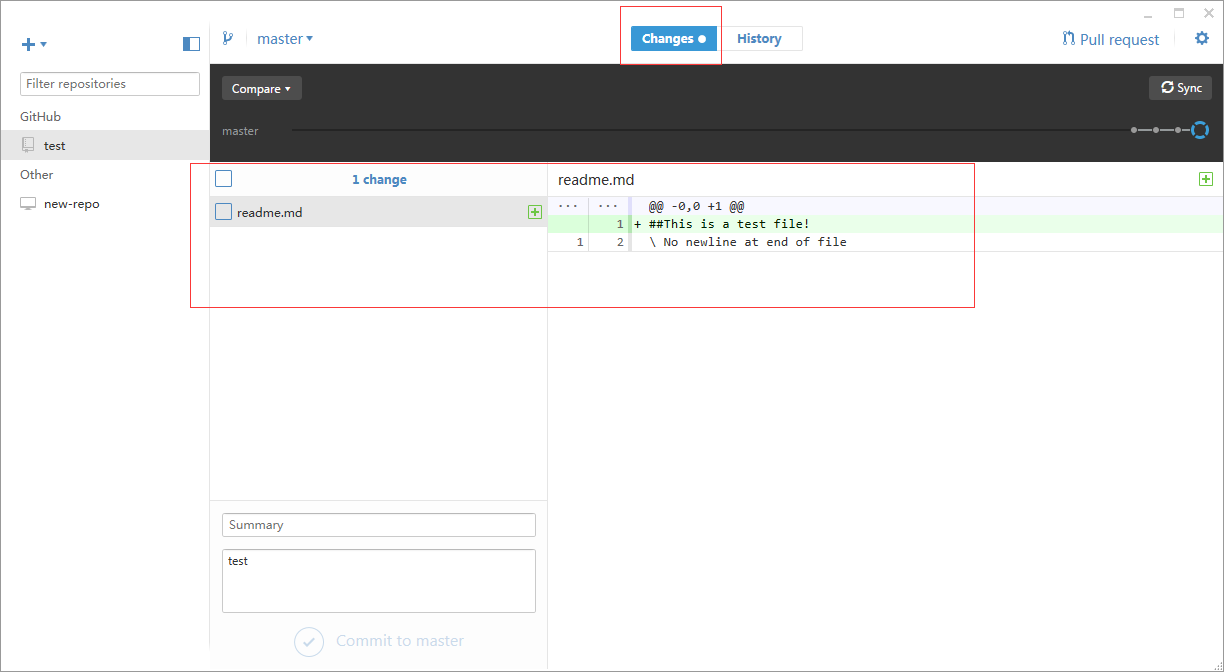
　　在左边文件栏里勾选你需要提交的文件，填写Summary和Description之后commit然后Sycn。然后你就可以在你的GitHub网页上看到新建的test仓库和里面添加的内容。

3.clone——clone版本库到本地

　　克隆很简单，如图点击"clone",会显示你远程仓库列表（注意这里是远程仓库的不是本地仓库）。

　　选中要clone的仓库，点击下方的"clone"按钮，会弹出一个文件窗口，选择从远程clone版本库的存放目录。

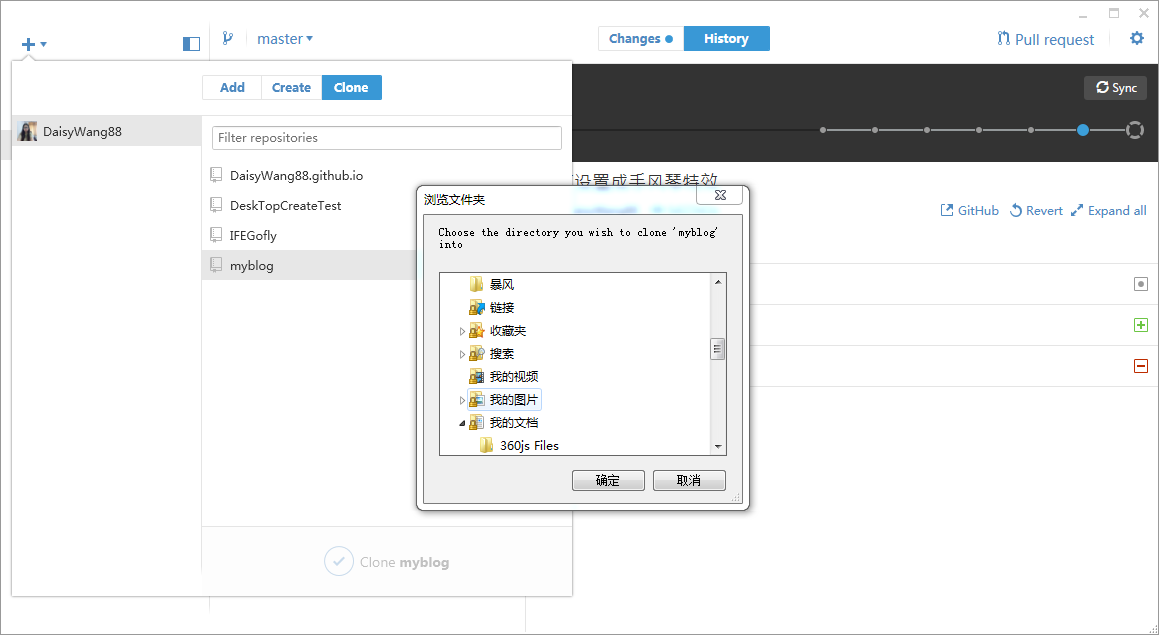
　　去查看你所选的目录会看到clone的版本库已经存在。

总结

　　GitHub DeskTop装起来比较慢，而且用起来经常卡，Git Bash比较轻量级速度比较快。用哪个根据个人喜好，但是最好不要混用，否则可能产生冲突，或者出错。比如，用Git Bash创建并连接的版本库，如果 add到GitHub DeskTop 修改文件之后commit就会失败。在如，用GitHub DeskTop  创建的版本库， add commit 都没有问题，因为这些都是在本地。push的时候会要求输入用户名，密码，输入之后依然出错。重新配置用户名和邮箱，再测试依然如此。