CORDIC算法（1）：圆周旋转模式下计算三角函数和模值

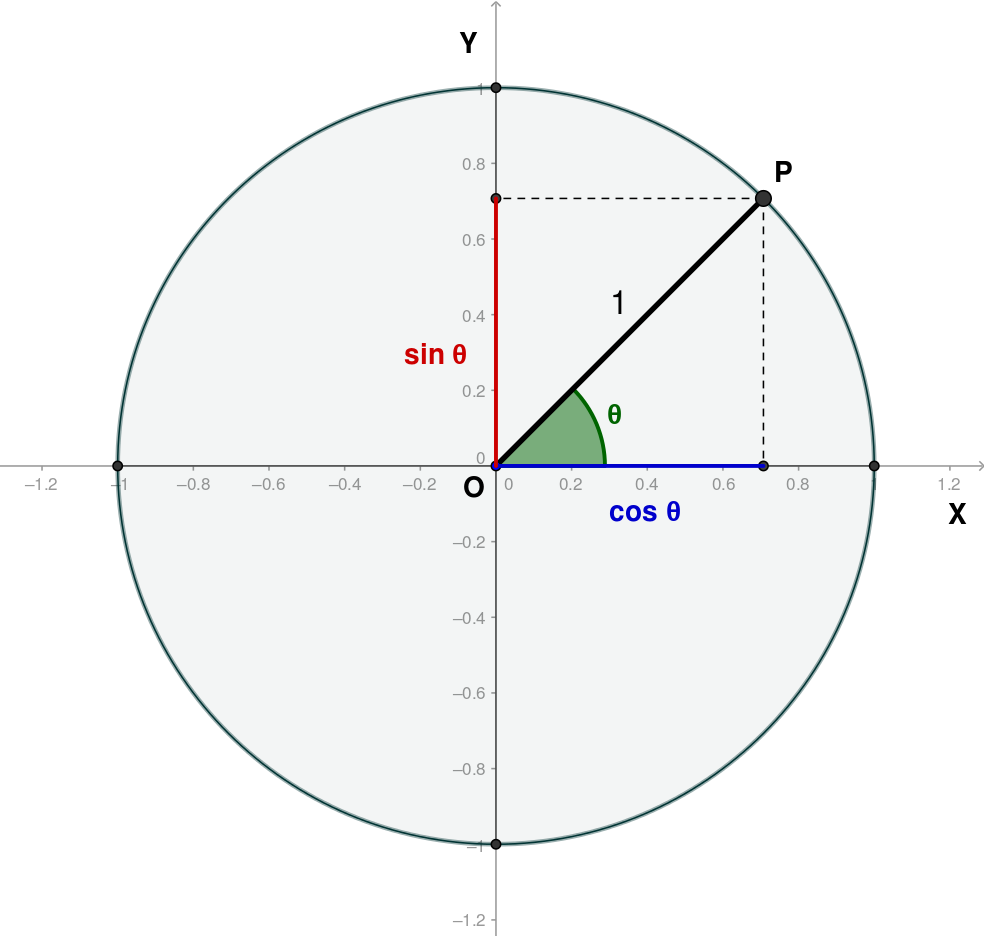
CORDIC（Coordinate Rotation Digital Computer）坐标旋转数字计算机，是数学与计算机技术交叉产生的一种机器算法，用于解决计算机的数学计算问题。发展到现在，CORDIC算法及其扩展算法大致有三种计算模式：圆周旋转模式、线性旋转模式和双曲线旋转模式，分别用来实现不同的数学运算。

本文介绍圆周旋转模式下的CORDIC算法原理及实现过程，另两种模式将分期介绍。

简单来讲，CORDIC利用近似逼近的思想，将计算机中三角函数、开根号、求对数等复杂运算，转化为简单的加减和移位操作。

对于实际只会识别0和1的计算机来说，加减和移位是它能轻松实现的操作，因此利用CORDIC算法将大大提升计算机对复杂运算的计算效率。目前，尽管计算机的运行速度已经足够使得大多数开发者不用太多考虑计算效率的问题，但在一些实时数据流比较大的场合（如通信、多媒体处理等），CORDIC算法依然是实现高速运算的关键。

类似CORDIC实现的数学思想早在1624年就由Henry Briggs提出并发表，但直到1956年，CORDIC算法才真正被美国工程师Jack E.Volder发现并运用，当时他正在寻找提高计算器计算精度和实时性的算法。直到1959年，Volder的算法才为公众所知，并在计算器上大行其道。

算法描述

1. 数学背景

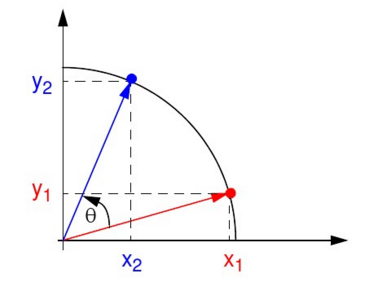
如图，XY平面中一点(x1,y1)经圆周旋转θ角度，得到点(x2,y2)。经简单的三角函数关系，可得到：

通过提出因数cosθ，可得：

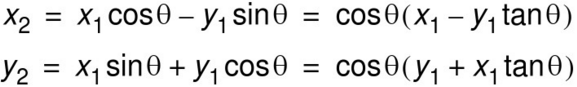
如果不考虑cosθ，得到“伪旋转”方程：

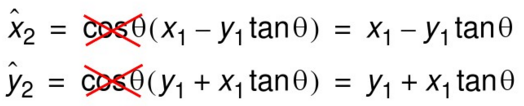
伪旋转仅实现了正确的角度旋转，但向量模值变为原来的1/cosθ。

2. CORDIC方法

若使得tanθ = 2^(-i)，i为自然数，则上式变为：

注意!上式已经仅剩加减和移位运算。

如果我们把所有tanθi = 2^(-i)对应的角度和正切值制成一张表，如下所示：

……

可以确定的是，任意旋转角度θ，都可以由上表中的大小不同θi进行多次旋转得到。CORDIC正是利用这一点，将θ角度的旋转分解为从大到小、逐次逼近真实旋转角度的一组旋转，而这些旋转的实现又都可以由加减和移位运算来完成。θi可以预先制成表格，供计算机查找使用。

算法实现

1. 已知坐标(x,y)，求其向量对应的相角θ（反正切）和模值

思想: 把原向量逐次向X正轴进行伪旋转逼近，整个过程的累计旋转角度即为θ，而旋转后的x坐标补偿模值增益K后即为原向量模值。

每次迭代的方程为：

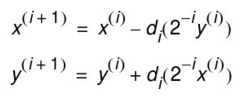
模值总增益K为：

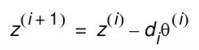
其中d决定旋转方向为逆时针还是顺时针，z为角度累加值。

注意！查找表中所有θi的总和约为99度，因此能实现计算的角度在-99~99度之间。实际算法实现时，我们可预先判断坐标象限，人为将其转化为第一象限内的计算，并在事后补偿为真实值。

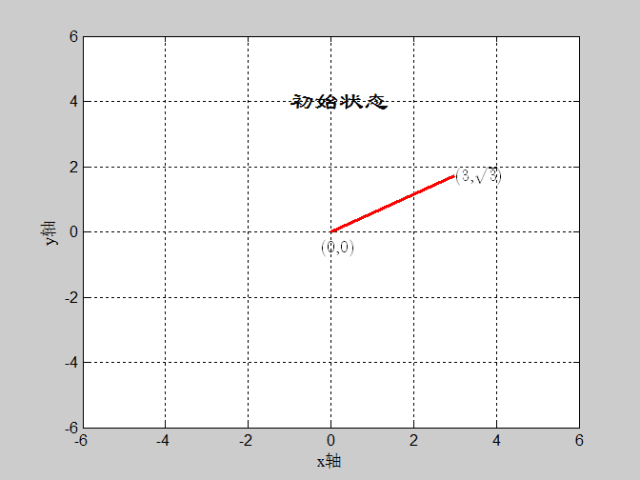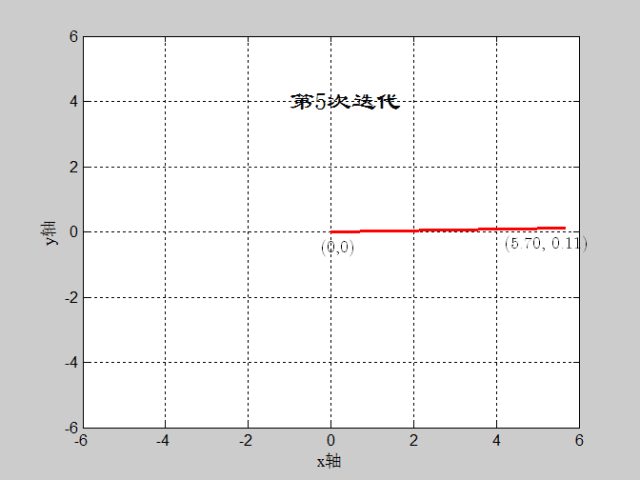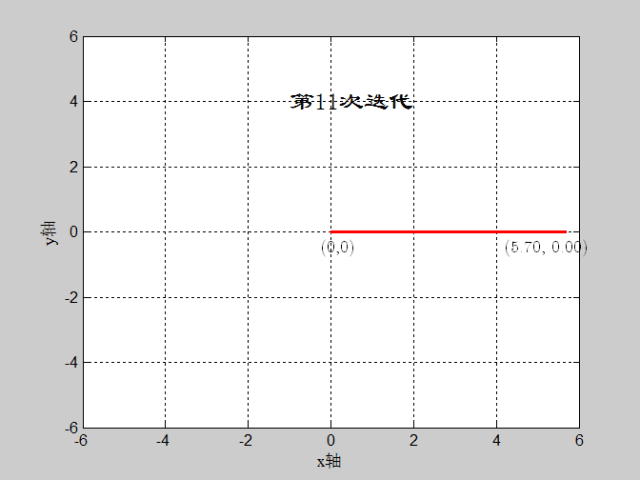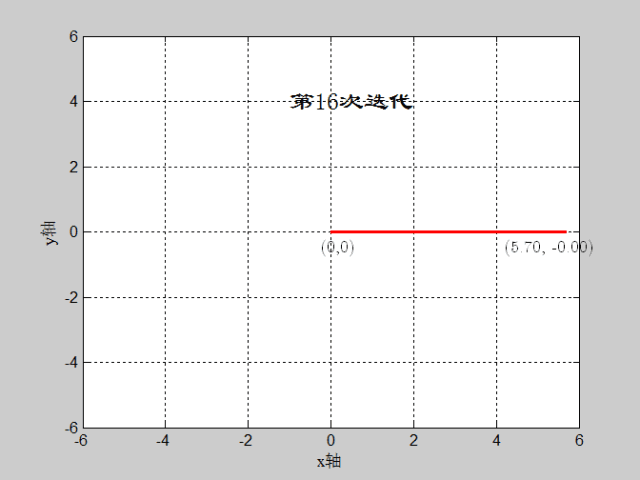
如图：(x,y)=(3,sqrt(3))，迭代深度=16，CORDIC算法实现过程

matlab代码如下：

%% ***********************************************************************************
%     已知坐标，用cordic算法计算相角和幅值。基本公式如下：
%     x(k+) = x(k) - d(k)*y(k)*^(-k)
%     y(k+) = y(k) + d(k)*x(k)*^(-k)
%     z(k) = z(k) - d(k)*actan(^(-k))
%% ***********************************************************************************  

clear;close all;clc;
% 初始化----------------------------------------
N = ;  %迭代次数
tan_table = .^-( : N-);
angle_LUT = atan(tan_table);  

K = ;
for k =  : N-
    K = K*(/sqrt( + ^(-*k)));
end  

x = ;
y = sqrt();
angle_accumulate = ;  

% cordic算法计算-------------------------------
if (x== && y==)
    radian_out = ;
    amplitude_out = ;
else  % 先做象限判断，得到相位补偿值
    if (x > )
        phase_shift = ;
    elseif (y < )
        phase_shift = -pi;
    else
        phase_shift = pi;
    end  

    for k =  : N-   % 迭代开始
        x_temp = x;
        if (y < )  % d(k)=，逆时针旋转
            x = x_temp - y*^(-k);
            y = y + x_temp*^(-k);
            angle_accumulate = angle_accumulate - angle_LUT(k+);
        else          % d(k)=-，顺时针旋转
            x = x_temp + y*^(-k);
            y = y - x_temp*^(-k);
            angle_accumulate = angle_accumulate + angle_LUT(k+);
        end
        radian_out = angle_accumulate + phase_shift; %弧度输出
    end  

    amplitude_out = x*K;  %幅值输出
end  

angle_out = radian_out*/pi;  %相角输出

2. 已知角度θ，求正弦sinθ和余弦cosθ

思想: 若向量模值为1，则其x坐标就是余弦值，y坐标就是正弦值。利用这一点，从(K,0)处迭代旋转至θ处的单位矢量即可。

迭代方程及K的计算同第一小节。同时也要注意预先对象限的判断和补偿。

如图：θ=60度，迭代深度=16，CORDIC算法实现过程

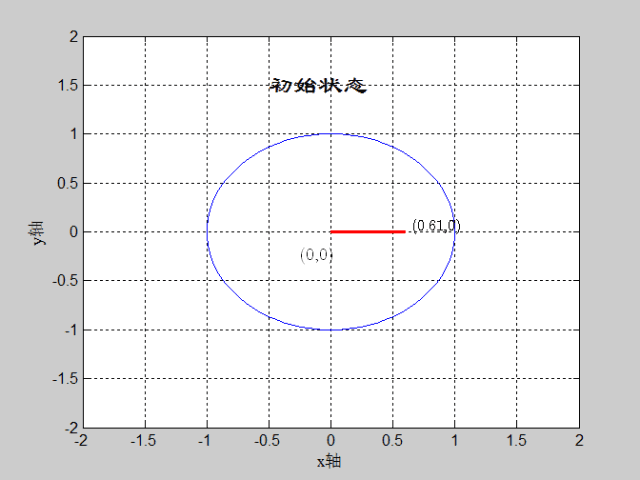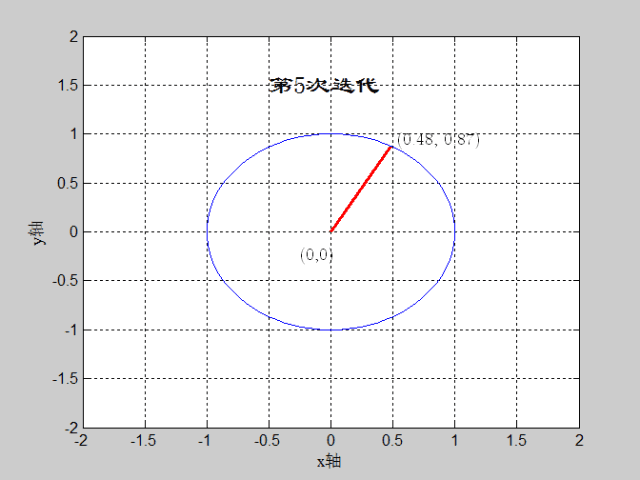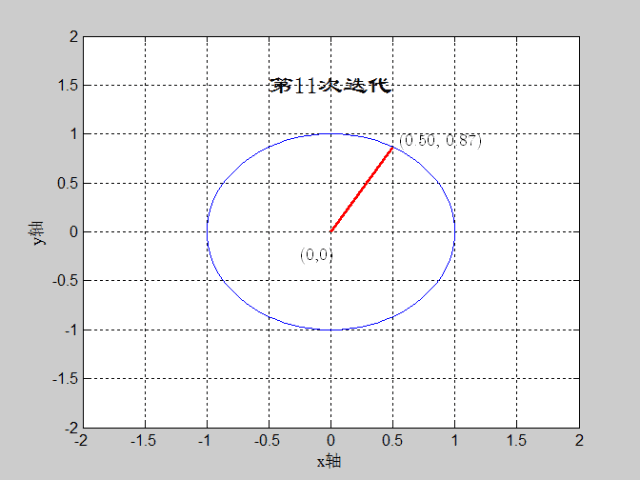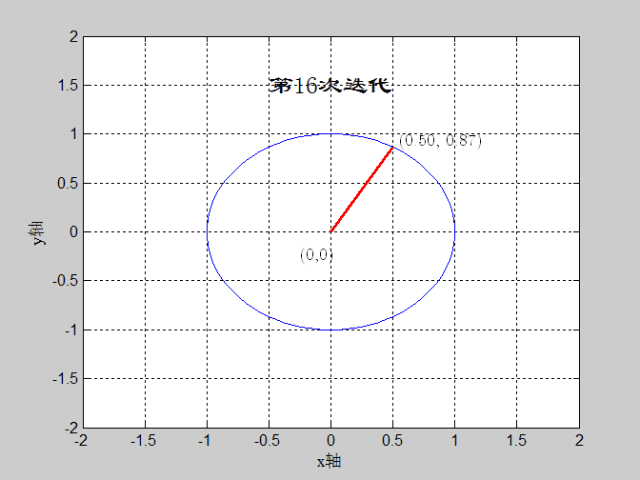
matlab代码如下：

%% ***********************************************************************************
%     已知相角theta，计算其正弦和余弦值。基本公式如下：
%     x(k+) = x(k) - d(k)*y(k)*^(-k)
%     y(k+) = y(k) + d(k)*x(k)*^(-k)
%     z(k) = z(k) - d(k)*actan(^(-k))
%% ***********************************************************************************
clear;close all;clc;  

% 初始化----------------------------------------
N = ;  %迭代次数
tan_table = .^-( : N-);
angle_LUT = atan(tan_table);  

K = ;
for k =  : N-
    K = K*(/sqrt( + ^(-*k)));
end  

theta = -;
x = ;
y = ;
phase_accumulate = theta/*pi;  %转化为弧度  

% cordic算法计算-------------------------------
if (phase_accumulate > pi/)  % 先做象限判断，得到相位补偿值
    phase_accumulate = phase_accumulate - pi;
    sign_x = -;
    sign_y = -;
elseif (phase_accumulate < -pi/)
    phase_accumulate = phase_accumulate + pi;
    sign_x = -;
    sign_y = -;
else
    sign_x = ;
    sign_y = ;
end  

 for k =  : N-   % 迭代开始
        x_temp = x;
        if (phase_accumulate > )  % d(k)=，逆时针旋转
            x = x_temp - y*^(-k);
            y = y + x_temp*^(-k);
            phase_accumulate = phase_accumulate - angle_LUT(k+);
        else                                     % d(k)=-，顺时针旋转
            x = x_temp + y*^(-k);
            y = y - x_temp*^(-k);
            phase_accumulate = phase_accumulate + angle_LUT(k+);
        end
end  

cos_out = sign_x*x*K;  %余弦输出
sin_out = sign_y*y*K;   %正弦输出

参考文献/资料

【1】https://en.wikipedia.org/wiki/CORDIC

【2】Xilinx CORDIC算法(非常经典)——百度文库

【3】ANDRAKA R. A Survey of CORDIC Algorithms for FPGA Based Computers[C] ，1998

·END·

欢迎来我的微信公众号做客：信号君

专注于信号处理知识、高性能计算、现代处理器&计算机体系

技术成长 | 读书笔记 | 认知升级

幸会~