最短路径——floyd(多源最短路径)
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <malloc.h> using namespace std; const int VERTEX_NUM = 20;
const int INFINITY = 0x7fffffff; bool vis[VERTEX_NUM];
int dist[VERTEX_NUM][VERTEX_NUM]; class Graph {
public:
int vexNum;
int edgeNum;
int vex[VERTEX_NUM];
int arc[VERTEX_NUM][VERTEX_NUM];
}; void createGraph(Graph &G)
{
cout << "please input vexNum and edgeNum: ";
cin >> G.vexNum >> G.edgeNum;
for (int i = 0; i != G.vexNum; ++i) {
cout << "please input no" << i+1 << " vertex: ";
cin >> G.vex[i]; // 自定义顶点序号
}
for (int i = 0; i != G.vexNum; ++i) {
for (int j = 0; j != G.vexNum; ++j) {
if (i == j) G.arc[i][j] = 0;
else G.arc[i][j] = INFINITY;
}
}
for (int k = 0; k != G.edgeNum; ++k) {
cout << "please input the vertex of edge(vi, vj) and weight: ";
int i, j, w;
cin >> i >> j >> w;
G.arc[i][j] = w;
G.arc[j][i] = G.arc[i][j];
}
} // Floyd算法
void floyd(Graph &G)
{
memset(dist, INFINITY, VERTEX_NUM);
for (int k = 0; k != G.vexNum; ++k) {
for (int i = 0; i != G.vexNum; ++i) {
for (int j = 0; j != G.vexNum; ++j) {
if (G.arc[i][j] > G.arc[i][k] + G.arc[k][j] && G.arc[i][k] < INFINITY && G.arc[k][j] < INFINITY) {
G.arc[i][j] = G.arc[i][k] + G.arc[k][j];
}
}
}
}
} int main()
{
Graph G;
createGraph(G);
floyd(G);
for (int i = 0; i != G.vexNum; ++i) {
for (int j = 0; j != G.vexNum; ++j) {
if (i == j) continue;
cout << "源点" << i << "到点" << j << "的距离为" << G.arc[i][j] << endl;
}
}
return 0;
}
时间复杂度:O(n3)
测试及结果:
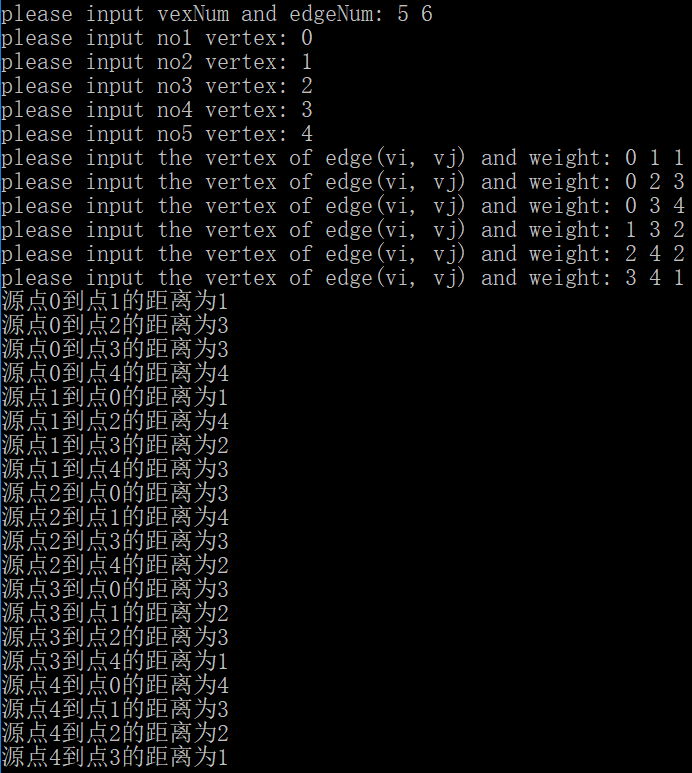
最短路径——floyd(多源最短路径)的更多相关文章
- 单源最短路径Dijkstra算法,多源最短路径Floyd算法
1.单源最短路径 (1)无权图的单源最短路径 /*无权单源最短路径*/ void UnWeighted(LGraph Graph, Vertex S) { std::queue<Vertex&g ...
- 经典贪心算法(哈夫曼算法,Dijstra单源最短路径算法,最小费用最大流)
哈夫曼编码与哈夫曼算法 哈弗曼编码的目的是,如何用更短的bit来编码数据. 通过变长编码压缩编码长度.我们知道普通的编码都是定长的,比如常用的ASCII编码,每个字符都是8个bit.但在很多情况下,数 ...
- 图->最短路径->多源最短路径(弗洛伊德算法Floyd)
文字描述 求每一对顶点间的最短路径,可以每次以一个顶点为源点,重复执行迪杰斯特拉算法n次.这样,便可求得每一对顶点之间的最短路径.总的执行时间为n^3.但是还有另外一种求每一对顶点间最短路径的方法,就 ...
- 多源最短路径Floyd算法
多源最短路径是求图中任意两点间的最短路,采用动态规划算法,也称为Floyd算法.将顶点编号为0,1,2...n-1首先定义dis[i][j][k]为顶点 i 到 j 的最短路径,且这条路径只经过最大编 ...
- 多源最短路径算法—Floyd算法
前言 在图论中,在寻路最短路径中除了Dijkstra算法以外,还有Floyd算法也是非常经典,然而两种算法还是有区别的,Floyd主要计算多源最短路径. 在单源正权值最短路径,我们会用Dijkstra ...
- [C++]多源最短路径(带权有向图):【Floyd算法(动态规划法)】 VS n*Dijkstra算法(贪心算法)
1 Floyd算法 1.1 解决问题/提出背景 多源最短路径(带权有向图中,求每一对顶点之间的最短路径) 方案一:弗洛伊德(Floyd算法)算法 算法思想:动态规划法 时间复杂度:O(n^3) 形式上 ...
- 多源最短路径算法:Floyd算法
前言 由于本人太菜,这里不讨论Floyd的正确性. 简介 多源最短路径,解决的是求从图中任意两点之间的最短路径的问题. 分析 代码短小精悍,主要代码只有四行,直接放上: for(int k=1;k&l ...
- 多源最短路径,一文搞懂Floyd算法
前言 在图论中,在寻路最短路径中除了Dijkstra算法以外,还有Floyd算法也是非常经典,然而两种算法还是有区别的,Floyd主要计算多源最短路径. 在单源正权值最短路径,我们会用Dijkstra ...
- Johnson 全源最短路径算法
解决单源最短路径问题(Single Source Shortest Paths Problem)的算法包括: Dijkstra 单源最短路径算法:时间复杂度为 O(E + VlogV),要求权值非负: ...
- Floyd-Warshall 全源最短路径算法
Floyd-Warshall 算法采用动态规划方案来解决在一个有向图 G = (V, E) 上每对顶点间的最短路径问题,即全源最短路径问题(All-Pairs Shortest Paths Probl ...
随机推荐
- shell编程基础-01
1.1 前言 1.1.1 为什么学Shell Shell脚本语言是实现Linux/UNIX系统管理及自动化运维所必备的重要工具Linux/UNIX系统的底层及基础应用软件的核心大都涉及Shell脚本的 ...
- canvas 将html绘制图片 生成图片链接
废话不多说,直接上代码 其中图片地址换成你的,自己玩儿去吧 <!DOCTYPE html> <html> <head> <meta charset=" ...
- ASP.NET Core学习网站推荐
跟大家推荐一个不错的学习.NET Core 的网站,这个网站的视频是付费的,但是录视频的都是.NET Core的大佬们,个人觉得很不错推荐出来 video.jessetalk.cn
- git创建使用1https://blog.csdn.net/Hanani_Jia/article/details/77950594
这篇文章是我自己写的关于GitHub的内容,从我刚听到这个直到设置成功每一步都有详细的步骤来解释,其中有一些截图或者代码来自于网上. 首先,我先对GitHub来一个简单的介绍,GitHub有一个很强大 ...
- django创建第一个子应用-3
在Web应用中,通常有一些业务功能模块是在不同的项目中都可以复用的,故在开发中通常将工程项目拆分为不同的子功能模块,各功能模块间可以保持相对的独立,在其他工程项目中需要用到某个特定功能模块时,可以将该 ...
- MySQL集群-PXC搭建以及使用innobackupex工具进行全局备份和增量备份
环境:centos7 vm1:10.154.47.236 vm2:10.154.52.189 vm3:10.105.12.50 目的:pxc使用三个节点构建mysql集群,使用innobackupex ...
- 『Python基础-4』字符串
# 『Python基础-4』字符串 目录 1.什么是字符串 2.修改字符串 2.1 修改字符串大小 2.2 合并(拼接)字符串 2.3 使用乘号'*'来实现字符串的叠加效果. 2.4 在字符串中添加空 ...
- Java8 Lambda表达式实战之方法引用(一)
方法的引用 方法引用是用来直接访问类或者实例的已经存在的方法或者构造方法,方法引用提供了一种引用而不执行方法的方式,如果抽象方法的实现恰好可以使用调用另外一个方法来实现,就有可能可以使用方法引用 方法 ...
- Caliburn.Micro 杰的入门教程2 ,了解Data Binding 和 Events(翻译)
Caliburn.Micro 杰的入门教程1(翻译)Caliburn.Micro 杰的入门教程2 ,了解Data Binding 和 Events(翻译)Caliburn.Micro 杰的入门教程3, ...
- java生成PDF,并下载到本地
1.首先要写一个PDF工具类,以及相关工具 2.PDF所需jar包 iText是一种生成PDF报表的Java组件 freemarker是基于模板来生成文本输出 <dependency> & ...
