POJ 1921 Paper Cut（计算几何の折纸问题）

Description

Still remember those games we played in our childhood? Folding and cutting paper must be among the most popular ones. Clever children will always search for something new, even when they play games like cutting paper. Now, Carol, a smart girl, asks her brother Mike to solve a puzzle. However, as always, Mike cannot find the solution, therefore he turns to you for help.

Carol's puzzle is simple to state. She folds the paper in a certain manner and then uses a knife to cut through the folded paper. What Mike needs to do is to tell how many pieces the folded paper will turn into after it is cut. To eliminate the ambiguity, we can coordinate the paper as [0, 1] * [0, 1], with the coordinates of lower left corner (0, 0). A fold is denoted by two points (x1, y1) and (x2, y2) on the folding line, with which, the direction of the line is determined by from (x1, y1) to (x2, y2). Carol will always fold the paper from left to right relative to the directed line given (see Figure-1). The cut is determined by the two points on the cut line. Please note that the points given to determine the fold or the cut are not necessarily on the paper.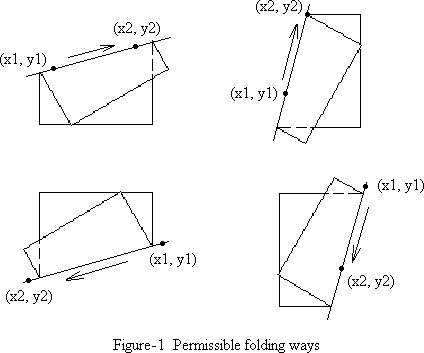 

Input

The first line of the input contains one integer t, the number of test cases. Then t cases follow. For each test case, the first line consists of an integer N (0 <= N <= 20), the number of folds, and the following N lines give two points on each fold line as x1, y1, x2, y2. The following line gives two points on the cut line in the same way.

Output

For each test case, output one line containing the number of pieces the paper will turn into after the cut.

 

题目大意：给一张正方形的纸，沿给出的n条线折叠n次，然后沿一条线切开，问切开后有多少张纸。（估计在折痕上切也可以把折痕切开）

思路：参考http://dumbear.com/blog/?p=249

主要是要理解上面所说的 本质不同的点。所谓本质不同的点，包括有两点虽然拥有同一个坐标，但是它们实际上是这张纸不同的点。

还有上面没有提到的，关于切割的时候，再折叠一次再切。

 

PS：好难……

 

代码（16MS）：

 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <iostream>
 #include <cmath>
 #include <vector>
 #include <map>
 using namespace std;
 typedef long long LL;
 typedef pair<int, int> PII;

 const double PI = acos(-1.0);
 const double EPS = 1e-;

 inline int sgn(double x) {
     return (x > EPS) - (x < -EPS);
 }

 struct Point {
     double x, y;
     Point() {}
     Point(double x, double y): x(x), y(y) {}
     void read() {
         scanf("%lf%lf", &x, &y);
     }
     Point operator + (const Point &rhs) const {
         return Point(x + rhs.x, y + rhs.y);
     }
     Point operator - (const Point &rhs) const {
         return Point(x - rhs.x, y - rhs.y);
     }
     Point operator * (double t) const {
         return Point(x * t, y * t);
     }
     double length() const {
         return sqrt(x * x + y * y);
     }
     Point unit() const {
         double l = length();
         return Point(x / l, y / l);
     }
 };

 double dist(const Point &p1, const Point &p2) {
     return (p1 - p2).length();
 }

 Point rotate(const Point &p, double angle, const Point &o = Point(, )) {
     Point t = p - o;
     double x = t.x * cos(angle) - t.y * sin(angle);
     double y = t.y * cos(angle) + t.x * sin(angle);
     return Point(x, y) + o;
 }

 double cross(const Point &a, const Point &b) {
     return a.x * b.y - a.y * b.x;
 }

 double cross(const Point &sp, const Point &ep, const Point &op) {
     return cross(sp - op, ep - op);
 }

 struct Seg {
     Point st, ed;
     Seg() {}
     Seg(Point st, Point ed): st(st), ed(ed) {}
     void read() {
         st.read(); ed.read();
     }
 };
 typedef Seg Line;
 //return Ax + By + C =0 's A, B, C
 void Coefficient(const Line &L, double &A, double &B, double &C) {
     A = L.ed.y - L.st.y;
     B = L.st.x - L.ed.x;
     C = L.ed.x * L.st.y - L.st.x * L.ed.y;
 }
 //point of intersection
 Point operator * (const Line &a, const Line &b) {
     double A1, B1, C1;
     double A2, B2, C2;
     Coefficient(a, A1, B1, C1);
     Coefficient(b, A2, B2, C2);
     Point I;
     I.x = - (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1);
     I.y =   (A2 * C1 - A1 * C2) / (A1 * B2 - A2 * B1);
     return I;
 }

 double Point_to_Line(const Point &p, const Line &L) {
     return fabs(cross(p, L.st, L.ed)/dist(L.st, L.ed));
 }

 Point reflection(const Point &p, const Line &l) {
     Point t = rotate(l.ed - l.st, -PI / );
     return p + t.unit() * ( * Point_to_Line(p, l));
 }

 vector<Point> p_vec, p_buf;

 struct Poly {
     vector<int> id;
     void add(int i) {
         id.push_back(i);
     }
     Point& operator [] (int i) const {
         return p_vec[id[i]];
     }
 };

 vector<Poly> pol_vec, pol_buf;
 map<PII, int> edge_map;

 Point paper[] = {Point(, ), Point(, ), Point(, ), Point(, )};

 void reflection(const Poly &pol, const Line &l) {
     for(int i = ; i < int(pol.id.size()); ++i)
         if(pol.id[i] < int(p_buf.size())) p_buf[pol.id[i]] = reflection(pol[i], l);
 }

 int intersection(int id1, int id2, const Point &p1, const Point &p2) {
     map<PII, int>::iterator it = edge_map.find(make_pair(id1, id2));
     if(it == edge_map.end()) {
         p_vec.push_back(Line(p_vec[id1], p_vec[id2]) * Line(p1, p2));
         edge_map[make_pair(id1, id2)] = edge_map[make_pair(id1, id2)] = p_vec.size() - ;
         return p_vec.size() - ;
     } else return it->second;
 }

 void fold(const Point &p1, const Point &p2, const Poly &pol) {
     Poly res1, res2;
     int last_s = sgn(cross(p1, pol[], p2));
     for(int i = ; i < int(pol.id.size()); ++i) {
         int now_s = sgn(cross(p1, pol[i], p2));
         if(now_s == ) {
             res1.add(pol.id[i]);
             res2.add(pol.id[i]);
         } else if(now_s < ) {
             if(last_s > ) {
                 int k = intersection(pol.id[i - ], pol.id[i], p1, p2);
                 res1.add(k);
                 res2.add(k);
             }
             res1.add(pol.id[i]);
         } else if(now_s > ) {
             if(last_s < ) {
                 int k = intersection(pol.id[i - ], pol.id[i], p1, p2);
                 res1.add(k);
                 res2.add(k);
             }
             res2.add(pol.id[i]);
         }
         last_s = now_s;
     }
     if(res1.id.size() > ) {
         res1.add(res1.id[]);
         reflection(res1, Line(p1, p2));
         reverse(res1.id.begin(), res1.id.end());
         pol_buf.push_back(res1);
     }
     if(res2.id.size() > ) {
         res2.add(res2.id[]);
         pol_buf.push_back(res2);
     }
 }

 void fold(const Point &p1, const Point &p2) {
     p_buf = p_vec;
     edge_map.clear();
     pol_buf.clear();
     for(int i = ; i < int(pol_vec.size()); ++i)
         fold(p1, p2, pol_vec[i]);
     pol_vec = pol_buf;
     for(int i = ; i < int(p_buf.size()); ++i)
         p_vec[i] = p_buf[i];
 }

 void dfs(vector<bool> &vis, int id, const Line &l) {
     vis[id] = true;
     Poly &pol = pol_vec[id];
     for(int i = ; i < int(pol.id.size() - ); ++i) {
         if(sgn(cross(l.ed, pol[i], l.st)) ==  && sgn(cross(l.ed, pol[i + ], l.st)) == ) continue;
         int id1 = pol.id[i], id2 = pol.id[i + ];
         for(int j = ; j < int(pol_vec.size()); ++j) {
             if(vis[j]) continue;
             for(int k = ; k < int(pol_vec[j].id.size() - ); ++k) {
                 if(pol_vec[j].id[k] == id1 && pol_vec[j].id[k + ] == id2) {
                     dfs(vis, j, l);
                     break;
                 }
             }
         }
     }
 }

 int cut(const Line &l) {
     int ret = ;
     vector<bool> vis(p_vec.size());
     for(int i = ; i < int(pol_vec.size()); ++i) {
         if(!vis[i]) {
             dfs(vis, i, l);
             ++ret;
         }
     }
     return ret;
 }

 int main() {
     int T;
     scanf("%d", &T);
     Poly init_pol;
     for(int i = ; i <= ; ++i) init_pol.add(i & );
     while(T--) {
         int n;
         scanf("%d", &n);
         p_vec.clear();
         pol_vec.clear();
         for(int i = ; i < ; ++i) p_vec.push_back(paper[i]);
         for(int i = ; i <= ; ++i) pol_vec.push_back(init_pol);
         Point p1, p2;
         for(int i = ; i <= n; ++i) {
             p1.read(), p2.read();
             fold(p1, p2);
         }
         printf("%d\n", cut(Line(p1, p2)));
     }
 }