leetcode 343. Integer Break(dp或数学推导)

Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.

For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).

Note: you may assume that n is not less than 2.

Hint:

1. There is a simple O(n) solution to this problem.
2. You may check the breaking results of n ranging from 7 to 10 to discover the regularities.

题意：给一个n(n>=2),求相加等于n且乘积最大的一组整数的积。

题解：

这其实就是一道高中数学题，但是leetcode上的数据比较水，导致完全不用数学推导的O(n²)的dp也可以过。

解法一（纯dp）：

令dp[n]为n对应的最大积。

那么递推方程就是：dp[n]=max(i*dp[n-i],i*(n-i))(其中i从1到n-1)。

边界:dp[2]=1;

时间复杂度：O(n²)

class Solution {
public:
    int integerBreak(int n) {
        int dp[n];
        dp[]=;
        dp[]=;
for(int i=;i<=n;i++){
            dp[i]=-;
            for(int j=;j<i;j++){
                dp[i]=max(j*dp[i-j],max(dp[i],j*(i-j)));
            }
        }
        return dp[n];
    }
};

解法二（当成数学题来做就好）：

由均值不等式(n个数的算术平均数大于等于它们的几何平均数)：

    >=   

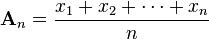得：当把输入的n拆分成几个相等的数时它们的积最大。

那么问题来了，拆分成几个呢？

为了方便使用导数，我们先假设我们可以把n拆分成实数。那么设每一个数为x,则一共有n/x个数。

设它们的积为f(x),则f(x)=x^(n/x)，那么怎么求f(x)最大值呢？求导数！

f′(x)=(n/x²)  *  x^(n/x)  * (1-lnx)

当x=e时取极大值。

而我们题目里规定x为整数，那么我们只需要取的x越靠近e越好。那么2<e<3，而且e=2.71828...，所以取3是最好的，如果取不到3就取2。

幂运算复杂度为O(lgn)，所以这个算法复杂度为O(lgn)。

class Solution {
public:
    int integerBreak(int n) {
        if(n == )
            return ;
        else if(n == )
            return ;
        else if(n% == )
            return pow(, n/);
        else if(n% == )
            return  *  * pow(, (n - ) / );
        else
            return  * pow(, n/);
    }
};