图连通性【tarjan点双连通分量、边双联通分量】【无向图】

根据 李煜东大牛：图连通性若干拓展问题探讨 ppt学习。

有割点不一定有割边，有割边不一定有割点。

理解low[u]的定义很重要。

1.无向图求割点、点双联通分量：

如果对一条边（x，y），如果low[y]>=dfn[x]，表示搜索树中y为根的子树必须要通过x才能到达树的上端，则x必为割点。

x属于多个点双联通分量，所以出栈的时候保留x（所以栈出到y就好！否则可能会把其他支路的节点一起出栈）。

附上一个小例子。

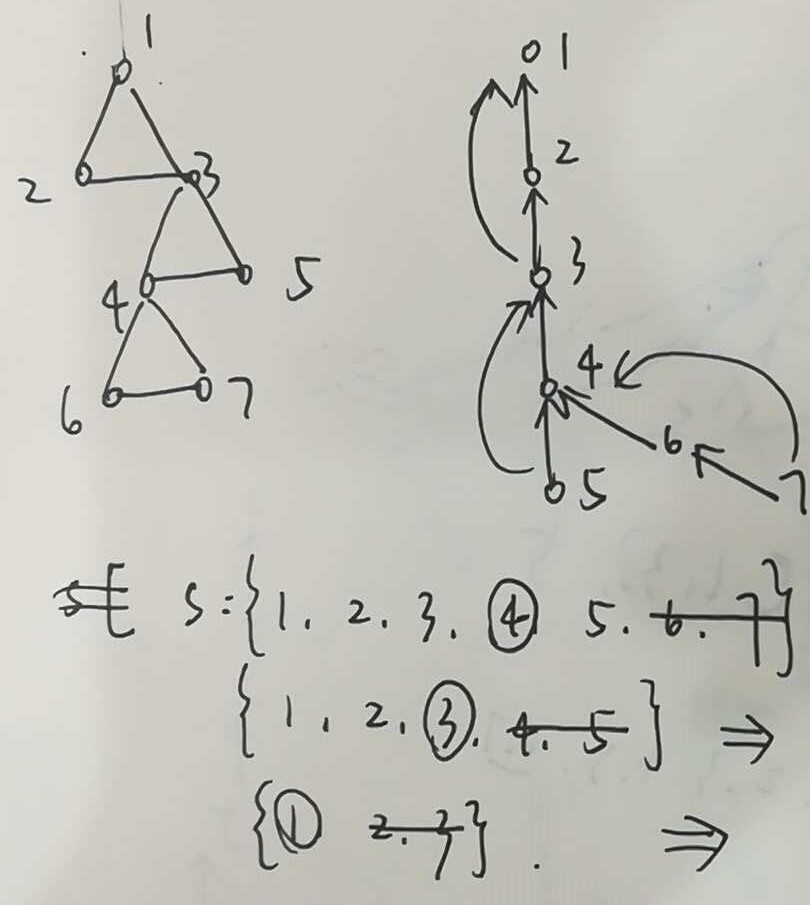
这个打个模板吧。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int N=;
 int n,m,al,cnt,num,sl,dfn[N],low[N],vis[N],s[N],first[N],b[N][];
 struct node{int x,y,next;}a[N*];

 void ins(int x,int y)
 {
     a[++al].x=x;a[++al].y=y;
     a[al].next=first[x];first[x]=al;
 }

 int minn(int x,int y){return x<y ? x:y;}

 void tarjan(int x)
 {
     dfn[x]=low[x]=++num;
     s[++sl]=x;
     for(int i=first[x];i;i=a[i].next)
     {
         int y=a[i].y;
         if(!dfn[y])
         {
             tarjan(y);
             low[x]=minn(low[x],low[y]);
             if(low[y]>=dfn[x])//key
             {
                 cnt++;
                 b[cnt][++b[cnt][]]=x;
                 while()
                 {
                     int z=s[sl--];
                     b[cnt][++b[cnt][]]=z;
                     if(z==y) break;
                 }
             }
         }
         else low[x]=minn(low[x],low[y]);
     }
 }

 int main()
 {
     freopen("a.in","r",stdin);
     scanf("%d%d",&n,&m);
     al=;
     memset(first,,sizeof(first));
     num=;cnt=;sl=;
     memset(dfn,,sizeof(dfn));
     memset(vis,,sizeof(vis));
     memset(b,,sizeof(b));
     for(int i=;i<=m;i++)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         ins(x,y);ins(y,x);
     }
     for(int i=;i<=n;i++)
         if(!dfn[i]) tarjan(i);
     for(int i=;i<=cnt;i++)
     {
         for(int j=;j<=b[i][];j++)
             printf("%d ",b[i][j]);
         printf("\n");
     }
     return ;
 }

2.无向图求割边、边双联通分量：

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int N=;
 int n,m,al,cnt,num,sl,dfn[N],low[N],vis[N],s[N],first[N],b[N][];
 struct node{int x,y,next,tmp;}a[N*];

 void ins(int x,int y)
 {
     a[++al].x=x;a[al].y=y;a[al].tmp=;
     a[al].next=first[x];first[x]=al;
 }

 int minn(int x,int y){return x<y ? x:y;}

 void tarjan(int x)
 {
     dfn[x]=low[x]=++num;
     s[++sl]=x;
     for(int i=first[x];i;i=a[i].next)
     {
         if(a[i].tmp) continue;
         a[i].tmp=;
         a[(i%)== ? i-:i+].tmp=;//key
         int y=a[i].y;
         if(!dfn[y])
         {
             tarjan(y);
             low[x]=minn(low[x],low[y]);
             if(low[y]>dfn[x])//key
             {
                 cnt++;
                 while()
                 {
                     int z=s[sl--];
                     b[cnt][++b[cnt][]]=z;
                     if(z==y) break;
                 }
             }
         }
         else low[x]=minn(low[x],low[y]);//前提：x->y不是搜索树上的边，故前面应该把走过的边的反向边去掉。
     }
 }

 int main()
 {
     //freopen("a.in","r",stdin);
     scanf("%d%d",&n,&m);
     al=;
     memset(first,,sizeof(first));
     num=;cnt=;sl=;
     memset(dfn,,sizeof(dfn));
     memset(vis,,sizeof(vis));
     memset(b,,sizeof(b));
     for(int i=;i<=m;i++)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         ins(x,y);ins(y,x);
     }
     for(int i=;i<=n;i++)
     {
         if(!dfn[i])
         {
             tarjan(i);
             if(sl) //key
             {
                 cnt++;
                 b[cnt][]=sl;
                 for(int j=;j<=sl;j++) b[cnt][j]=s[j];
                 sl=;
             }
         }
     }
     for(int i=;i<=cnt;i++)
     {
         for(int j=;j<=b[i][];j++)
             printf("%d ",b[i][j]);
         printf("\n");
     }
     return ;
 }