[SRM568]DisjointSemicircles

题意：$2n$个位置排成一列，有一些位置已经填了数字（$0\cdots n-1$中每个数字出现$0$次或$2$次），问是否存在一种填数方案使得用$n$个不相交的半圆可以把相同的数字连起来

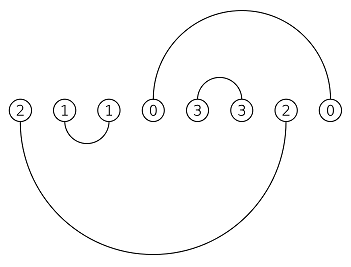
首先把所有已经填了的数字的半圆画出来，如果两个半圆相交那么它们必须在异侧，在相交的半圆之间连边，如果不是二分图那么就无解

我们用$-1$代表未填数的位置，给$-1$的位置分配$1$代表这个位置向上连线，$0$代表这个位置向下连线

朴素的想法是：对于每个半圆$[l,r]$，枚举它在上方还是在下方，如果在上方，那么$[l,r]$中必须有偶数个$1$，如果在下方，那么$[l,r]$中必须有偶数个$0$（用$-1$的个数减去$0$的个数即可得到$1$的个数），并且因为对于每个不是$-1$的位置$i$，因为不能给它分配$1$，所以$[i,i]$中必须有偶数个$0$，最后，显然所有位置上必须有偶数个$1$

现在问题变为：给定一些区间$[l,r]$和对其中$1$的个数的奇偶性要求，问是否能满足，求异或前缀和后就变成对一些变量的异或值限制，直接dfs一遍看是否冲突即可

但是这样会很慢，考虑优化

如果一个半圆$[l,r]$不与其他半圆相交，当区间长度为偶数时，它放在上或下都要求区间中$1$的个数是偶数，当区间长度为奇数时，放在上或下可以使得区间中$1$的个数是奇数或是偶数，又因为它和其他半圆互不影响，所以我们这样处理：如果区间长度为奇数，不管它，如果区间长度为偶数，那么我们不用枚举它放在上还是下，直接令区间中$1$的个数是偶数即可

所以我们只用对二分图中大小$\geq2$的连通块枚举它的两半分别在上还是下，因为最多有$\frac n2$个半圆，所以最多有$\frac n4$个大小$\geq2$的连通块，所以总时间复杂度为$O(n2^{\frac n4})$

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<vector>
#include<string>
using namespace std;
struct seg{
	int l,r;
	seg(int a=0,int b=0){l=a;r=b;}
}e[30];
bool ints(seg a,seg b){
	if(a.l>b.l)swap(a,b);
	return b.l<a.r&&b.r>a.r;
}
vector<int>vt[30][2];
vector<int>sg;
int cnt;
struct graph{
	int h[30],nex[610],to[610],M,n;
	void reset(){
		M=0;
		memset(h,0,sizeof(h));
	}
	void ins(int a,int b){
		M++;
		to[M]=b;
		nex[M]=h[a];
		h[a]=M;
	}
	void add(int a,int b){
		ins(a,b);
		ins(b,a);
	}
	int c[30];
	bool dfs(int x,int f){
		if(~c[x])return c[x]==f;
		vt[cnt][f].push_back(x);
		c[x]=f;
		for(int i=h[x];i;i=nex[i]){
			if(!dfs(to[i],f^1))return 0;
		}
		return 1;
	}
	bool gao(int n){
		sg.clear();
		memset(c,-1,sizeof(c));
		cnt=0;
		for(int i=1;i<=n;i++){
			if(c[i]==-1){
				if(h[i]){
					vt[cnt][0].clear();
					vt[cnt][1].clear();
					if(!dfs(i,0))return 0;
					cnt++;
				}else
					sg.push_back(i);
			}
		}
		return 1;
	}
}g;
struct graph2{
	int h[60],nex[210],to[210],v[210],M;
	void reset(){
		M=0;
		memset(h,0,sizeof(h));
	}
	void ins(int a,int b,int c){
		M++;
		to[M]=b;
		v[M]=c;
		nex[M]=h[a];
		h[a]=M;
	}
	void add(int a,int b,int c){
		ins(a,b,c);
		ins(b,a,c);
	}
	int c[60];
	bool dfs(int x,int f){
		if(~c[x])return c[x]==f;
		c[x]=f;
		for(int i=h[x];i;i=nex[i]){
			if(!dfs(to[i],f^v[i]))return 0;
		}
		return 1;
	}
	bool gao(int n){
		memset(c,-1,sizeof(c));
		for(int i=0;i<=n;i++){
			if(c[i]==-1&&!dfs(i,0))return 0;
		}
		return 1;
	}
}g2;
int a[60],s[60];
class DisjointSemicircles{
	public:
		string getPossibility(vector<int>v){
			int n,i,j,M;
			n=v.size();
			M=0;
			for(i=1;i<=n;i++){
				a[i]=v[i-1];
				s[i]=s[i-1]+(a[i]==-1);
				if(~a[i]){
					for(j=1;j<i;j++){
						if(a[j]==a[i])break;
					}
					if(i!=j)e[++M]=seg(j,i);
				}
			}
			g.reset();
			for(i=1;i<M;i++){
				for(j=i+1;j<=M;j++){
					if(ints(e[i],e[j]))g.add(i,j);
				}
			}
			if(!g.gao(M))return"IMPOSSIBLE";
			for(i=0;i<1<<cnt;i++){
				g2.reset();
				for(int x:sg){
					if((e[x].r-e[x].l)&1)g2.add(e[x].l-1,e[x].r,0);
				}
				for(j=0;j<cnt;j++){
					for(int x:vt[j][i>>j&1])g2.add(e[x].l-1,e[x].r,0);
					for(int x:vt[j][~i>>j&1])g2.add(e[x].l-1,e[x].r,(s[e[x].r]-s[e[x].l-1])&1);
				}
				for(j=1;j<=n;j++){
					if(~a[j])g2.add(j-1,j,0);
				}
				g2.add(0,n,0);
				if(g2.gao(n))return"POSSIBLE";
			}
			return"IMPOSSIBLE";
		}
};
/*
int main(){
	int x;
	DisjointSemicircles cl;
	vector<int>v;
	for(scanf("%d",&x);x!=-2;scanf("%d",&x))v.push_back(x);
	puts(cl.getPossibility(v).c_str());
}
*/