C语言复习---迭代法，牛顿迭代法，二分法求根

一：用迭代法求 x=√a。求平方根的迭代公式为：X(n+1)=(Xn+a/Xn) /2。

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main()
{
    double x1, x2;
    float a;
    scanf("%f", &a);
    x2 = 1.0;
    do
    {
        x1 = x2;
        x2 = (x1 + a / x1) / 2;
    } while (fabs(x1-x2)>pow(10,-5));
    printf("value:%lf", x2);
    system("pause");
    return ;
}

二：用牛顿迭代法求方程在1.5附近的根（2x³-4x²+3x-6=0）

例：方程求根牛顿迭代法 求方程 f(x)=x3+x2-3x-3=0在1.5附近的根

f(x)=x^+x^-3x-
f'(x)=3x^2+2x-3
x(n+)=xn-f(xn)/f'(xn)
令x1=1.5
x2=1.777778
x3=1.733361
x4=1.732052
x5=1.732051
x6=1.732051
如果精确到0.,则x=1.732051
准确值=根号3

重要公式

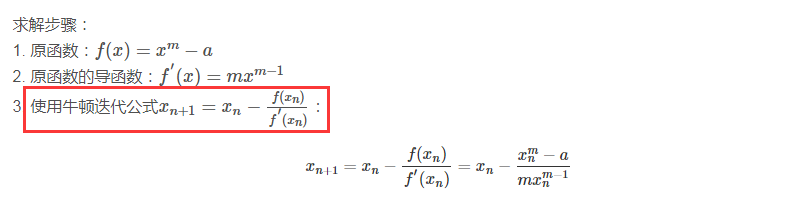
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main()
{
    double x1=, x2;
    double fx1, fx2;
    x2 = 1.5;
    while (fabs(x1 - x2)>=1e-)
    {
        x1 = x2;
        fx1 =  * x1*x1*x1 -  * x1*x1 +  * x1 - ;　　//f(xn)
        fx2 =  * x1*x1 -  * x1 + ;　　　　　　　　　　　//f(xn)'
        x2 = x1 - fx1 / fx2;
    }
    printf("value:%lf", x2);
    system("pause");
    return ;
}

三：二分法求方程的根

给定精确度ξ,用二分法求函数f(x)零点近似值的步骤如下:
 确定区间[a,b],验证f(a)·f(b)<0（这是前提，选取的区间必须满足这个条件）,给定精确度ξ.
 求区间(a,b)的中点c.
 计算f(c).

() 若f(c)=,则c就是函数的零点;
() 若f(a)·f(c)<,则令b=c;
() 若f(c)·f(b)<,则令a=c.
() 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double fx(double x)
{
    return  * x*x*x -  * x*x +  * x - ;
}

int main()
{
    double x1 , x2;
    double fx1, fx2;
    double e = 1e-;

    do
    {
        printf("enter (x1,x2):\n");
        scanf("%lf", &x1);
        scanf("%lf", &x2);
        if (x1>x2)
        {
            double temp = x1;
            x1 = x2;
            x2 = temp;
        }
        fx1 = fx(x1);
        fx2 = fx(x2);
    } while (fx1*fx2>);

    if (fabs(fx1) < e)
        printf("solution1:%lf\n", x1);
    else if (fabs(fx2) < e)
        printf("solution2:%lf\n", x2);
    else
    {
        while (fabs(x1 - x2) >= e)
        {
            double mid = (x1 + x2) / ;
            if (fx(mid)*fx2 < )
                x1 = mid;
            else
                x2 = mid;
        }
        printf("solution3:%lf", x2);
    }
    system("pause");
    return ;
}