2018.11.05 bzoj3124: [Sdoi2013]直径（树形dp）

传送门

一道sbsbsb树形dpdpdp

第一问直接求树的直径。

考虑第二问问的边肯定在同一条直径上均是连续的。

因此我们将直径记下来。

然后对于直径上的每一个点，dpdpdp出以这个点为根的子树中不走与直径上的节点能得到的最大深度来求出那一段合法边的范围。

那么有些什么情况呢？

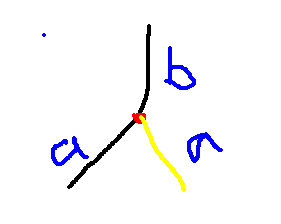
1. 分出了一条跟这个点下面那段直径一样长的那么满足条件的区域最下端不能低于这个点。
2. 分出了一条跟这个点上面那段直径一样长的那么满足条件的区域最上端不能高于这个点。
   
   代码：

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int ans=0;
	char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
	return ans;
}
typedef long long ll;
const int N=2e5+5;
int n,cnt=0,first[N],bg=0,ed=0,fa[N],line[N],tot=0,down=-0x3f3f3f3f,up=0x3f3f3f3f;
bool vis[N];
ll dis[N],Dis[N];
struct edge{int v,next;ll w;}e[N<<1];
inline void add(int u,int v,ll w){e[++cnt].v=v,e[cnt].w=w,e[cnt].next=first[u],first[u]=cnt;}
void dfs1(int p,int pre){
	for(int i=first[p];i;i=e[i].next){
		int v=e[i].v;
		if(v==pre)continue;
		dis[v]=dis[p]+e[i].w,dfs1(v,p);
	}
	if(dis[p]>dis[bg])bg=p;
}
void dfs2(int p){
	for(int i=first[p];i;i=e[i].next){
		int v=e[i].v;
		if(v==fa[p])continue;
		fa[v]=p,dis[v]=dis[p]+e[i].w,dfs2(v);
	}
	if(dis[p]>dis[ed])ed=p;
}
void dfs3(int p,int pre){
	Dis[p]=dis[p];
	for(int i=first[p];i;i=e[i].next){
		int v=e[i].v;
		if(v==pre||vis[v])continue;
		dfs3(v,p),Dis[p]=max(Dis[p],Dis[v]);
	}
}
int main(){
	n=read();
	for(int i=1,u,v,w;i<n;++i)u=read(),v=read(),w=read(),add(u,v,(ll)w),add(v,u,(ll)w);
	dfs1(1,0),dis[bg]=0,dfs2(bg);
	for(int i=ed;i;i=fa[i])vis[line[++tot]=i]=1;
	for(int i=1;i<=tot;++i){
		dfs3(line[i],0);
		if(Dis[line[i]]==dis[line[1]])down=max(down,i);
		if(Dis[line[i]]==dis[line[i]]*2)up=min(up,i);
	}
	cout<<dis[ed]<<'\n'<<up-down;
	return 0;
}