HGOI20180904（NOIP2018模拟sxn出题）

sol

输入n和H表示n个人，选H个人gcd最大
抓住排列，是x[1,n]的正整数，是连续的整数，
假设现在最大的公因数是k其中k一定是在[1,n]那么在排列中最多出现的个数为w
那么kw是最大的含有因数k的数字满足kw<=n所以k<=n/w
显然w越小答案k越大而w取值范围是[H,n]所以w=H时答案最大
所以 k(max)=n/H
由于选的序号最小那么for一遍按顺序输出即可
复杂度O（n）

# include <bits/stdc++.h>
using namespace std;
const int MAXN=;
int a[MAXN];
int main()
{
    freopen("dst.in","r",stdin);
    freopen("dst.out","w",stdout);
    int n,k;
    scanf("%d%d",&n,&k);
    for (int i=;i<=n;i++) scanf("%d",&a[i]);
    int temp=n/k; printf("%d\n",temp);
    int cnt=;
    for (int i=;i<=n;i++)
     if (!(a[i]%temp)) {
         printf("%d ",i),cnt++;
         if (cnt==k) break;
     }
    return ;
}

sol

设F[i]为斐波那契数列的第i项，显然f[i]=f[i-2]+f[i-1]
一个有趣的结论 gcd(f[a],f[b])=f[gcd([a],[b])]
证明：
设n<m，设第f(n)与f(n+1)为a,b，则有：
首先 证明：gcd(F[n+1],F[n])=1;
辗转相减法：
gcd(F[n+1],F[n])
=gcd(F[n+1]-F[n],F[n])
=gcd(F[n],F[n-1])
=gcd(F[2],F[1])
=1

x     f(x)

5
...
n      a
n+1    b
n+   a+b
n+   a+2b
n+   2a+3b
n+   3a+5b
...
m     f[m-n-1]a+f[m-n]b

因为gcd(m,n)=gcd(n,m%n)

所以 gcd(f(m),f(n))=gcd(f(n),f(m)%f(n))=gcd(a,f(m-n)b)

a,b相邻 gcd(a,b)=1;

f(n)=a【逃这应该看得出来吧】
gcd(f(m),f(n))=gcd(f(n),f(m-n)）
辗转相减法 就是gcd(f(n),f(m%n))
辗转相除法 就是f(gcd(n,m))
对于20%的数据，0＜n,m＜100000 随便线性推一推就行
对于60%的随机数据 ，找到规律线性递推求斐波那契数列即可
对于100%的数据 n,m＜=10^14，找到规律，用矩阵快速幂优化递推就行
单位矩阵这样的：

f[i-] f[i-]             f[i] f[i-]
                                  

复杂度O（log n）

# include <bits/stdc++.h>
using namespace std;
typedef  long long ll;
const int mo=,MAXN=;
struct Node{
    ll m[][];
};
Node tt;
ll gcd(ll a,ll b)
{
    return b==?a:gcd(b,a%b);
}
Node mul(Node a,Node b)
{
    Node t;
    for (int i=;i<=;i++)
     for (int j=;j<=;j++)
      {
          ll sum=;
          for (int k=;k<=;k++)
          sum=(sum+a.m[i][k]*b.m[k][j]%mo)%mo;
          t.m[i][j]=sum%mo;
      }
    return t;
}
Node pow(Node x,ll n)
{
    if (n==) return tt;
    Node t=pow(x,n/);
    t=mul(t,t);
    if (n%==) t=mul(t,x);
    return t;
}
int main()
{
    freopen("st.in","r",stdin);
    freopen("st.out","w",stdout);
    /*
     f[] a,b g=gcd(a,b);
     f[g]=gcd[f[a],f[b]];
    */
    ll n,m; scanf("%lld%lld",&n,&m);
    if (n>m) swap(n,m);
    ll g=gcd(n,m);
    if (g==1ll||g==2ll) {
        printf("1\n");
        return ;
    }
    Node k;
    k.m[][]=,k.m[][]=;
    k.m[][]=;k.m[][]=;
    tt=k;
    Node w=pow(k,n-);
    printf("%lld\n",w.m[][]%mo);
    return ;
}

sol

错排问题的模板问题
假设A...为信封，a...为信件
我假设把a放B里，显然是一个错放，在这里我们可以看到这个错误出现的类型有两大类：（
就是导致这个错放的原因）

• b错放到A里，此时，b错放到A；a错放到B；后面的C..和A,B没有关系了，后面n-2个信封全错排 就是f(n-2)
• b错放到除了A、B之外的一个信封，剩下的n-1个信封全错排就能符合条件放法总数为f(n-1)

　　总而言之，在a错放到B里，共有错放法：f(n-2)+f(n-1)这么多种，
在a错放到C，错放到D……(n－1)种可能的情况下，同样有f(n-2)+f(n-1)种错放法，因此得出错放总数为
　　 f(n)=(n-1){f(n-2)+f(n-1)}

复杂度O(n)

# include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mo=1e9+,MAXN=;
ll f[MAXN];
int main()
{
    freopen("jdt.in","r",stdin);
    freopen("jdt.out","w",stdout);
    int n;
    while(~scanf("%d",&n)) {
        f[]=;f[]=;
        for (int i=;i<=n;i++)
         f[i]=(i-)*((f[i-]+f[i-])%mo)%mo;
        printf("%lld\n",f[n]);
    }
    return ;
}

二项式反演

上个公式：

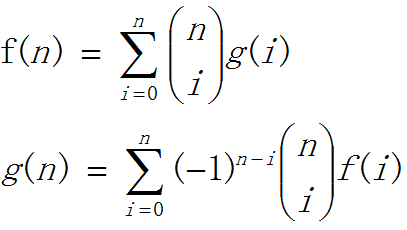
f(n)表示n个数的全排列，即 f(n)=n!
g(i)有n个信封中有i个信封错排，g(n)就是我们要求的结果。

f(n)= C(n,0)g(0) + C(n,1) g(1) ….+C(n,n) * g(n)
从n里面选0,1,2...n错排总数和就是全排列
因为对于全排列有2种可能：
1.正确摆放 （1）
2.有i个错误摆放 (0<i<=n)
归纳一下就是有i个错误摆放 (0=<i<=n)

反演一下就ok
g(n)=∑(-1)^(n-i) * C(n,i) * i! (从0到n)
C(n,i)的时候暴力搞一下逆元。

复杂度O(n)

std是这种方法：

#include <cstdio>
#include <algorithm>
#include <iostream>
#define LL long long
using namespace std;
int n;
const LL MOD=1e9+;
const int MAXN=;
LL f[MAXN],t[MAXN];
void fff(){
    freopen("jdt.in","r",stdin);
    freopen("jdt.out","w",stdout);
}
void fction(){
    f[]=;
    for (int i=;i<=;i++)f[i]=(f[i-]*i)%MOD;
    t[]=t[]=;
    for (int i=;i<=;i++)t[i]=((MOD-MOD/i)%MOD)*(t[MOD%i]%MOD)%MOD;
    for (int i=;i<=;i++) t[i]=(t[i]*t[i-])%MOD;
}
int main(){
    fff();
    fction();
    while (scanf("%d",&n)!=EOF){
        LL ans=;
        LL flag=n&?-:;
        for (int i=;i<=n;i++){
            ans=(ans+(flag*1ll*((f[n]%MOD)*t[n-i])%MOD))%MOD;
            flag=-flag;
        }
        ans=(ans+MOD)%MOD;
        printf("%lld\n",ans);
    }
}