【中文分词】条件随机场CRF

之前介绍的MMEM存在着label bias问题，因此Lafferty et al. [1] 提出了CRF (Conditional Random Field). BTW：比较有意思的是，这篇文章的二作与三作同时也是MEMM的作者。

1. 前言

本节将遵从tutorial [2] 的论文结构，从概率模型（Probabilistic Models）与图表示（Graphical Representation）两个方面引出CRF。

概率模型

Naïve Bayes（NB）是分类问题中的生成模型（generative model），以联合概率\(P(x,y)=P(x|y)P(y)\)建模，运用贝叶斯定理求解后验概率\(P(y|x)\)。NB假定输入\(x\)的特征向量\((x^{(1)},x^{(2)},\cdots,x^{(j)},\cdots, x^{(n)})\)条件独立（conditional independence），即

\begin{equation}

P(x|y) P(y) = P(y) \prod _{j} P(x^{(j)}|y)

\label{eq:nb}

\end{equation}

HMM是用于对序列数据\(X\)做标注\(Y\)的生成模型，用马尔可夫链（Markov chain）对联合概率\(P(X,Y)\)建模：

\begin{equation}

P(X,Y) = \prod_t P(y_t|y_{t-1}) P(x_t|y_t)

\label{eq:hmm}

\end{equation}

然后，通过Viterbi算法求解\(P(Y|X)\)的最大值。LR (Logistic Regression)模型是分类问题中的判别模型（discriminative model），直接用logistic函数建模条件概率\(P(y|x)\)。实际上，logistic函数是softmax的特殊形式（证明参看ufldl教程），并且LR等价于最大熵模型（这里给出了一个简要的证明），完全可以写成最大熵的形式：

\begin{equation}

P_w(y|x) = \frac{exp \left( \sum_i w_i f_i(x,y) \right)}{Z_w(x)}

\label{eq:me}

\end{equation}

其中，\(Z_w(x)\)为归一化因子，\(w\)为模型的参数，\(f_i(x,y)\)为特征函数（feature function）——描述\((x,y)\)的某一事实。

CRF便是为了解决标注问题的判别模型，于是就有了下面这幅张图（出自 [3]）：

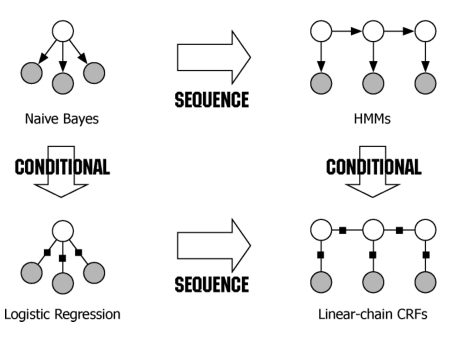
图表示

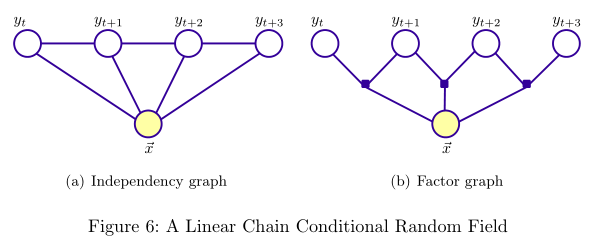
概率模型可以用图表示变量的相关（依赖）关系，所以概率模型常被称为概率图模型（probabilistic graphical model, PGM）。PGM对应的图有两种表示形式：independency graph, factor graph. independency graph直接描述了变量的条件独立，而factor graph则是通过因子分解（ factorization）的方式暗含变量的条件独立。比如，NB与HMM所对应的两种图表示如下（图出自[2]）：

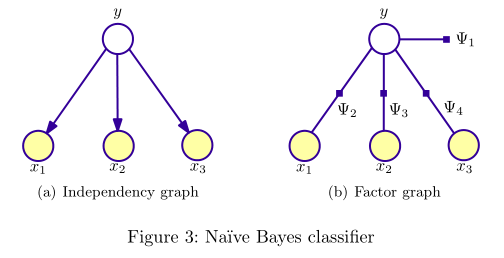
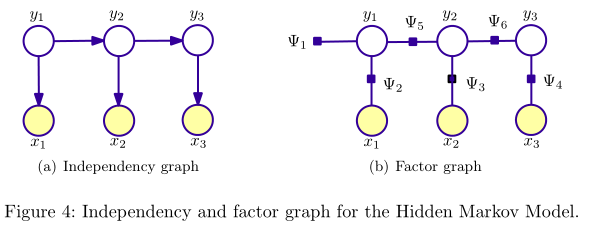
可以看出，NB与HMM所对应的independency graph为有向图，图\((V, E)\)所表示的联合概率\(P(\overrightarrow{v})\)计算如下：

\[P(\overrightarrow{v}) = \prod_k P(v_k|v_k^p)
\]

其中，\(v_k\)为图\((V, E)\)中一个顶点，其parent节点为\(v_k^p\)。根据上述公式，则上图中NB模型的联合概率:

\[P(y,x_1, x_2, x_3) = P(y)P(x_1|y)P(x_2|y)P(x_3|y)
\]

有别于NB模型，最大熵则是从全局的角度来建模的，“保留尽可能多的不确定性，在没有更多的信息时，不擅自做假设”；特征函数则可看作是人为赋给模型的信息，表示特征\(x\)与\(y\)的某种相关性。有向图无法表示这种相关性，则采用无向图表示最大熵模型：

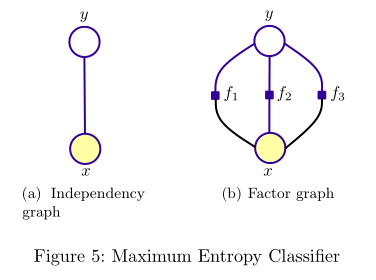
最大熵模型与马尔可夫随机场（Markov Random Field, MRF）所对应factor graph都满足这样的因子分解：

\begin{equation}

P(\overrightarrow{v}) = \frac{\prod_C \Psi_C(\overrightarrow{v_C})}{Z}

\label{eq:mrf}

\end{equation}

其中，\(C\)为图的团（即连通子图），\(\Psi_C\)为势函数（ potential function）。在最大熵模型中，势函数便为\(exp(w_i f_i(x,y))\)的形式了。

2. CRF

前面提到过，CRF（更准确地说是Linear-chain CRF）是最大熵模型的sequence扩展、HMM的conditional求解。CRF假设标注序列\(Y\)在给定观察序列\(X\)的条件下，\(Y\)构成的图为一个MRF，即可表示成图：

根据式子\eqref{eq:mrf}，则可推导出条件概率：

\[P(Y|X) = \frac{\prod_j \Psi_j(\overrightarrow{x}, \overrightarrow{y})}{Z(\overrightarrow{x})}
\]

同最大熵模型一样，因子\(\Psi_j(\overrightarrow{x}, \overrightarrow{y})\)亦可以写成特征函数的exp形式：

\[\Psi_j(\overrightarrow{x}, \overrightarrow{y}) = \exp \left( \sum_i \lambda_i f_i(y_{j-1}, y_j, \overrightarrow{x}) \right)
\]

特征函数之所以定义成\(f_i(y_{j-1}, y_j, \overrightarrow{x})\)而非$ f_i(y_j, \overrightarrow{x})$，是因为Linear-chain CRF对随机场做了Markov假设。那么，CRF建模的式子可改写为

\[\begin{aligned}
P(Y|X) & = \frac{\exp \left( \sum_{i,j} \lambda_i f_i(y_{j-1}, y_j, \overrightarrow{x}) \right)}{Z(\overrightarrow{x})} \\
& = \frac{1}{Z(\overrightarrow{x})} \prod_j \exp \left( \sum_{i} \lambda_i f_i(y_{j-1}, y_j, \overrightarrow{x}) \right)
\end{aligned}
\]

MMEM也是用最大熵模型建模\(P(Y|X)\)， 不同于CRF的是其采用有向图模型，只考虑\(x_j\)对\(y_j\)的影响，而没有把\(x\)作为整体来考虑，导致的是本地归一化：

\[P(Y|X) = \prod_j \frac{\exp \left( \sum_{i} \lambda_i f_i(y_{j-1}, y_j, \overrightarrow{x}) \right)}{Z(y_{j-1},\overrightarrow{x})}
\]

而CRF做的则是全局的归一化，避免了label bias的问题。

3. 开源实现

Genius是一个基于CRF的开源中文分词工具，采用了Wapiti做训练与序列标注。

import genius

text = "深夜的穆赫兰道发生一桩车祸，女子丽塔在车祸中失忆了"
seg_list = genius.seg_text(text)
print('/'.join([w.text for w in seg_list]))
# 深夜/的/穆赫兰道/发生/一/桩/车祸/，/女子/丽塔/在/车祸/中/失忆/了  [CRF]
# 深夜/的/穆赫/兰/道/发生/一/桩/车祸/，/女子/丽塔/在/车祸/中/失忆/了  [2-HMM]
# 深夜/的/穆赫兰道/发生/一桩/车祸/，/女子丽塔/在/车祸/中/失忆/了  [HMM]

可以看出，CRF在处理未登录词比HMM的效果是要好的。当然，你可以用CRF++自己撸一个中文分词器。正好，52nlp的有一篇教程教你如何撸，用的是bakeoff2005 的训练语料 msr_training.utf8。

---

Footnote: CRF原论文 [1] 与李航老师的《统计学习方法》关于CRF的推导引出，显得比较突兀。相反，tutorial [2] 将NB、HMM、maxent (LR)与CRF串联在一起，从Probabilistic Models、Graphical Representation的角度论述，非常容易理解——CRF是如何在考虑\(Y\)的相关性时对条件概率\(P(Y|X)\)建模的；为一篇不得不读的经典的CRF tutorial。

4. 参考资料

[1] Lafferty, John, Andrew McCallum, and Fernando Pereira. "Conditional random fields: Probabilistic models for segmenting and labeling sequence data." Proceedings of the eighteenth international conference on machine learning, ICML. Vol. 1. 2001.

[2] Klinger, Roman, and Katrin Tomanek. Classical probabilistic models and conditional random fields. TU, Algorithm Engineering, 2007.

[3] Sutton, Charles, and Andrew McCallum. "An Introduction to Conditional Random Fields." Machine Learning 4.4 (2011): 267-373.

[4] shinchen2, 统计模型之间的比较. （为转载链接）

[5] KevinXU, 如何理解马尔可夫随机场里因子的表达？