广度优先(bfs)和深度优先搜索(dfs)的应用实例

广度优先搜索应用举例：计算网络跳数

图结构在解决许多网络相关的问题时直到了重要的作用。

比如，用来确定在互联网中从一个结点到另一个结点（一个网络到其他网络的网关）的最佳路径。一种建模方法是采用无向图，其中顶点表示网络结点，边代表结点之间的联接。使用这种模型，可以采用广度优先搜索来帮助确定结点间的最小跳数。

如图1所示，该图代表Internet中的6个网络结点。以node1作为起点，有不止1条可以通往node4的路径。<node1,node2,node4>，<node1,node3,node2,node4>，<node1,node3,node5,node4>都是可行的路径。广度优先搜索可以确定最短路径选择，即<node1,node2,node4>，一共只需要两跳。

我们以bfs作为广度优先搜索的函数名（见示例1及示例2）。该函数用来确定互联网中两个结点之间的最小跳数。这个函数有3个参数：graph是一个图，在这个问题中就代表整个网络；start代表起始的顶点；hops是返回的跳数链表。函数bfs会修改图graph，因此，如果有必要的话在调用该函数前先对图创建拷贝。另外，hops中返回的是指向graph中实际顶点的指针，因此调用者必须保证只要访问hops，graph中的存储空间就必须保持有效。

graph中的每一个顶点都是一个BfsVertex类型的结构体（见示例1），该结构体有3个成员：data是指向图中顶点的数据域指针，color在搜索过程中维护顶点的颜色，hops维护从起始顶点开始到目标顶点的跳数统计。

match函数是由调用者在初始化graph时作为参数传递给graph_init的。match函数应该只对BfsVertex结构体中的data成员进行比较。

bfs函数将按照前面介绍过的广度优先搜索的方式来计算。为了记录到达每个顶点的最小跳数，将每个顶点的hop计数设置为与该顶点邻接的顶点的hop计数加1。对于每个发现的顶点都这样处理，并将其涂成灰色。每个顶点的颜色和跳数信息都由邻接表结构链表中的BfsVertex来维护。最后，加载hops中所有跳数未被标记为-1的顶点。这些就是从起始顶点可达的顶点。

bfs的时间复杂度为O（V+E），这里V代表图中的顶点个数，E是边的个数。这是因为初始化顶点的颜色属性以及确保起始顶点存在都需要O（V）的运行时间，广度优先搜索中的循环的复杂度是O（V+E），加载跳数统计链表的时间为O（V）。

示例1：广度优先搜索的头文件

/*bfs.h*/
#ifndef BFS_H
#define BFS_H

#include "graph.h"
#include "list.h"

/*定义广度优先搜索中的顶点数据结构*/
typedef struct BfsVertex_
{
    void *data;
    VertexColor color;
    int hops;
}BfsVertex;

/*函数接口定义*/
int bfs(Graph *graph, BfsVertex *start, List *hops);

#endif // BFS_H

示例2：广度优先搜索的实现

/*bfs.c*/
#include <stdlib.h>
#include "bfs.h"
#include "graph.h"
#include "list.h"
#include "queue.h"

/*bfs */
int bfs(Graph *graph, BfsVertex *start, List *hops)
{
    Queue     queue;
    AdjList   *adjlist, *clr_adjlist;
    BfsVertex *clr_vertex, *adj_vertex;
    ListElmt  *element, *member;

    /*初始化图中的所有结点为广度优先结点*/
    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        clr_vertex = ((AdjList *)list_data(element))->vertex;
        if(graph->match(clr_vertex,start))
        {
            /*初始化起始顶点*/
            clr_vertex->color = gray;
            clr_vertex->hops  = ;
        }
        else
        {
            /*初始化非起始顶点*/
            clr_vertex->color = white;
            clr_vertex->hops = -;
        }
    }
    /*初始化队列，并将起始顶点的邻接表入队*/
    queue_init(&queue,NULL);
        /*返回起始顶点的邻接表，存储到clr_adjlist*/
    if(graph_adjlist(graph,start,&clr_adjlist) != )
    {
        queue_destroy(&queue);
        return -;
    }
        /*将顶点的邻接表入队到队列*/
    if(queue_enqueue(&queue,clr_adjlist) !=  )
    {
        queue_destroy(&queue);
        return -;
    }

    /*执行广度优先探索*/
    while(queue_size(&queue) > )
    {
        adjlist = queue_peek(&queue);

        /*遍历邻接表中的每一个顶点*/
        for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(member))
        {
            adj_vertex = list_data(member);

            /*决定下一个邻接点的颜色*/
            if(graph_adjlist(graph,adj_vertex,&clr_adjlist) != )
            {
                queue_destroy(&queue);
                return -;
            }
            clr_vertex = clr_adjlist->vertex;

            /*把白色的顶点标成灰色，并把它的邻接顶点入队*/
            if(clr_vertex->color == white)
            {
                clr_vertex->color = gray;
                clr_vertex->hops = ((BfsVertex *)adjlist->vertex)->hops + ;

                if(queue_enqueue(&queue,clr_adjlist) != )
                {
                    queue_destroy(&queue);
                    return -;
                }
            }
        }

        /*将当前顶点邻接表从队列中移除并涂成黑色*/
        if(queue_dequeue(&queue,(void **)&adjlist) == )
        {
            ((BfsVertex *)adjlist->vertex)->color = black;
        }
        else
        {
            queue_destroy(&queue);
            return -;
        }
    }

    queue_destroy(&queue);

    /*返回每一个顶点的hop计数到一个链表中*/
    list_init(hops,NULL);

    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        /*跳过那些没有被访问到的节点（hops = -1）*/
        clr_vertex = ((AdjList *)list_data(element))->vertex;
        if(clr_vertex->color != -)
        {
            if(list_ins_next(hops,list_tail(hops),clr_vertex) != )
            {
                list_destroy(hops);
                return -;
            }
        }
    }
    return ;
}

深度优先搜索的应用举例：拓扑排序

有时候，我们必须根据各种事物间的依赖关系来确定一种可接受的执行顺序。比如，在大学里必须满足一些先决条件才能选的课程，或者一个复杂的项目，其中某个特定的阶段必须在其他阶段开始之前完成。要为这一类问题建模，可以采用优先级图，其采用的是有向图的思路。在优先级图中，顶点代表任务，而边代表任务之间的依赖关系。以必须先完成的任务为起点，以依赖于此任务的其他任务为终点，画一条边即可。

如下图所示，它表示7门课程及其先决条件组成的一份课程表：S100没有先决条件，S200需要S100，S300需要S200和M100，M100没有先决条件，M200需要M100，M300需要S300和M200，并且S150没有先决条件同时也不是先决条件。

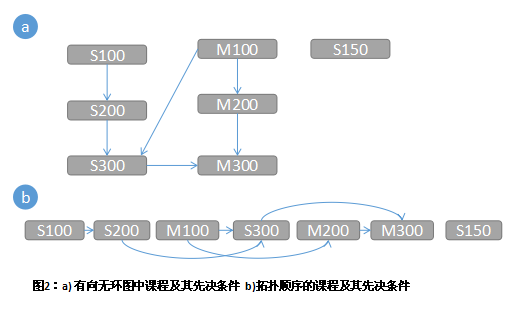
通过对这些课程执行拓扑排序，深度优先搜索有助于确定出一中可接受的顺序。

拓扑排序将顶点排列为有向无环图，因此所有的边都是从左到右的方向。正规来说，有向无环图G=(V,E)的拓扑排序是其顶点的一个线性排序，以便如果G中存在一条边（u，v），那么线性顺序中u出现在v的前面，在许多情况下，满足此条件的顺序有多个。

下面的代码示例实现了函数dfs，即深度优先搜索。该函数在这里用来对任务做拓扑排序。dfs有两个参数：graph代表图，在这个问题中则代表需要排序的任务；而参数ordered是完成拓扑排序后返回的顶点链表。调用该函数会修改图graph，因此如果有必要需要在调用前先对graph创建一个副本。另外，函数返回后链表ordered中保存了指向图graph中顶点的指针，因此调用者必须保证，一旦访问ordered中的元素就必须保证graph中的存储空间保持有效。graph中的每一个顶点都是一个DfsVertex结构体，该结构体拥有两个成员：data是指向顶点数据域部分的指针；而color在搜索过程中负责维护顶点的颜色信息。match函数是由调用者在初始化graph时通过参数传递给graph_init的，该函数应该只对DfsVertex结构体中的data成员进行比较。

dfs按照深度优先的方式进行搜索。dfs_main是实际执行搜索的函数。dfs中的最后一个循环保证对图中所有未相连的元素完成了检索。在dfs_main中逐个完成顶点的搜索并将其涂黑，然后插入链表ordered的头部。最后，ordered就包含完整拓扑排序后的顶点。

dfs的时间复杂度是O（V+E），V代表图中的顶点个数，而E代表边的个数。这是因为初始化顶点的颜色信息需要O（V）的时间，而dfs_main的时间复杂度为O（V+E）。

示例3：深度优先搜索的头文件

/*dfs.h*/
#ifndef DFS_H
#define DFS_H

#include "graph.h"
#include "list.h"

/*为深度优先搜索中的所有节点定义一个结构体*/
typedef struct DfsVertex_
{
    void *data;
    VertexColor color;
}DfsVertex;

/*公共接口*/
int dfs(Graph *graph,List *ordered);

#endif // DFS_H

 示例4：深度优先搜索的函数实现

/*dfs.c*/
#include <stdlib.h>

#include "dfs.h"
#include "graph.h"
#include "list.h"

/*dfs_main*/
static int dfs_main(Graph *graph, AdjList *adjlist, List *ordered)
{
    AdjList   *clr_adjlist;
    DfsVertex *clr_vertex, *adj_vertex;
    ListElmt  *member;

    /*首先，将起始顶点涂成灰色，并遍历它的邻接顶点集合*/
    ((DfsVertex *)adjlist->vertex)->color = gray;

    for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(member))
    {
        /*决定下一个集合顶点的颜色*/
        adj_vertex = list_data(member);

        if(graph_adjlist(graph,adj_vertex,&clr_adjlist) != )
        {
            return -;
        }

        clr_vertex = clr_adjlist->vertex;
        /*如果当前顶点是白色，则递归搜索它的邻接点*/
        if(clr_vertex->color == white)
        {
            if(dfs_main(graph,clr_adjlist,ordered) != )
                return -;
        }
    }

    /*把当前顶点涂成“黑”色，并加入到链表头部*/
    ((DfsVertex *)adjlist->vertex)->color = black;

    if(list_ins_next(ordered, NULL, (DfsVertex *)adjlist->vertex) != )
        return -;

    return ;
}

/*dfs*/
int dfs(Graph *graph, List *ordered)
{
    DfsVertex *vertex;
    ListElmt  *element;

    /*初始化图中的所有顶点*/
    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        vertex = ((AdjList *)list_data(element))->vertex;
        vertex->color = white;
    }

    /*执行广度优先搜索*/
    list_init(ordered,NULL);

    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        /*确保图中的每个顶点都能被检索到*/
        vertex = ((AdjList *)list_data(element))->vertex;

        if(vertex->color == white)
        {
            if(dfs_main(graph, (AdjList *)list_data(element), ordered) != )
            {
                list_destroy(ordered);
                return -;
            }
        }
    }

    return ;
}