深度优先搜索DFS和广度优先搜索BFS简单解析（新手向）

深度优先搜索DFS和广度优先搜索BFS简单解析

与树的遍历类似，图的遍历要求从某一点出发，每个点仅被访问一次，这个过程就是图的遍历。图的遍历常用的有深度优先搜索和广度优先搜索，这两者对于有向图和无向图均适用。

一.深度优先搜索

1.理解分析

首先，让我们来看一看更些简单的深度优先搜索DFS。顾名思义，这个搜索方法是以深度优先，也就是先一条路走到黑，撞到南墙再回头。我们可以看做是一棵树，优先走到根部，然后换一根继续走到最后。下面给出一张图便于理解。

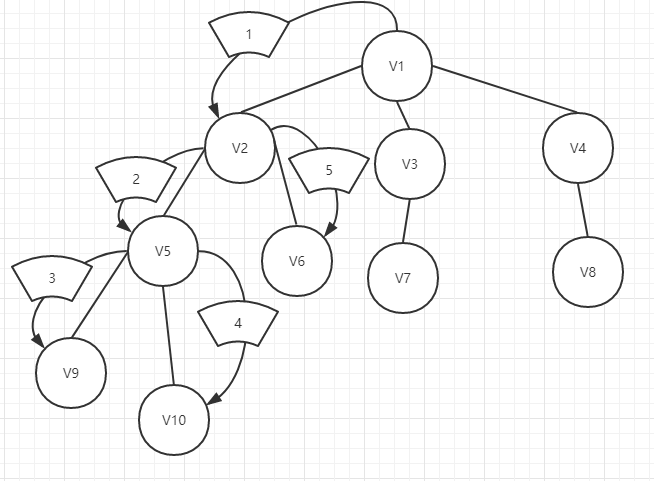
我们可以看到，我们先从V1出发前往V2，然后继续往更深的地方出发，前往V5，V9，然后由于V9是根的最深处，于是我们返回上一层（V5所在），发现还有一个V10没有搜索，所以我们前往V10，然后由于V10是最深的地方，接着往回上一层（V5所在），看看是否还有没有访问搜索的点，发现没有，接着返回上一层（V2所在），发现还有一个V6没有访问，于是搜索访问V6。如此重复，这样就是深度优先搜索。

我们来仔细思考下这个过程，有没有发现和递归有着类似之处？

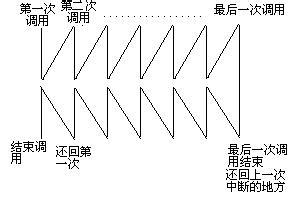
我们来看一看，第一次调用，我们可以理解为目前处于第二层搜索V2节点，第二次调用，我们可以理解为DFS里搜索该节点下的第三层节点，调用完成后结束调用可以看做返回第一层，这样，其中一条V2及以下都已经被遍历过，重复过程，改变参数，我们可以使得所有都被遍历过一次。所以，我们一般采用递归的方法来实现DFS。

2.例题分析

https://vjudge.net/problem/HDU-1241

油田问题可以说是经典的使用DFS解决的问题了。

Input：

Output:

2

输入的第一行是油田行数和列数，@符号代表油田，我们要求的是的 @ 符号连成一块地（横竖斜相连都算），能有几块这样的油田地。

下面给出代码：

#include<iostream>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
int map[150][150];//用来记录该地是否被查询过，0代表没有
int x, y;
char p[150][150];//存放油田
int find(int a, int m, int n)
{
	if (map[m][n] != 0|| p[m][n] != '@')//当不是油田（也就是搜索到头了），并且被找过了，则返回0
		return 0;
	else
	{
		map[m][n] = a;
        //下面这些就是递归部分，写成这样分开便于理解
		//先一直往横坐标加1，往右侧不断查询，以下同理
		find(a, m + 1, n);
		find(a, m + 1, n + 1);
		find(a, m + 1, n - 1);
		find(a, m, n + 1);
		find(a, m, n - 1);
		find(a, m - 1, n + 1);
		find(a, m - 1, n);
		find(a, m - 1, n - 1);
	}
	return 0;
}
int oilPocket(int a)
{
	int i, j;
	for (i = 0; i < x; i++)
	{
		for (j = 0; j < y; j++)
		{
			if (map[i][j] == 0 && p[i][j] == '@')
			{   //当遇到一块油田没有被遍历过，则以这个点进行深度优先搜索
				find(a, i, j);//a代表这块大油田地是第几块，ij就是坐标
				a++;
			}
		}
	}
	return a;
}
int main()
{
	int ans;
	while (scanf("%d %d", &x, &y) != EOF)
	{
		if (x == 0 || y == 0) break;
		memset(p, '*', sizeof(p));
		for (int i = 0; i < x; i++)
		{
			cin.get();//存回车
			for (int j = 0; j < y; j++)
			{
				scanf("%c", &p[i][j]);
			}
		}
		memset(map, 0, sizeof(map));
		ans = oilPocket(1) - 1;
		printf("%d\n", ans);
	}
	return 0;
}

这段代码主要是find函数部分，我们可以看到，每次递归都是一开始往右侧找，找到头后往下找，每次都是有着固定的方向，一路寻找到头，然后才会改变方向。这样，我们就使用DFS成功地求得连接在一起的油田数量。

• 有一点在写深度优先搜索时容易犯错误，那就是注意要判断该点是否查询过，反复查询会导致无限递归从而程序出现错误。

二.广度优先搜索

1.理解分析

和深度优先搜索不同的是，我们先访问的是同一层未被搜索过的点，当该层搜索完毕后，我们才会往下一层进发，开始下一层的搜索。

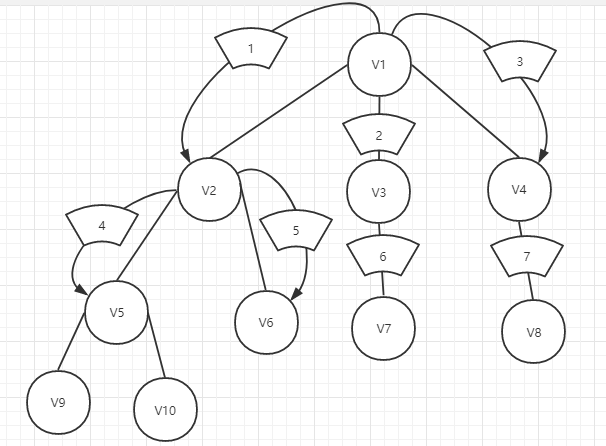
由图我们可以看到我们从V1开始，选择搜索V2，接下来并没有同深度优先搜索一样，搜索V5，而是接着看看同层是否有未被搜索过的点，我们发现V3没有被搜索过，所以我们接着搜索V3，知道V3，V4都被搜索过，我们才开始往下一层进发，搜索V5，V6......

接着，我们来仔细想想，我们该怎么实现BFS呢？

我们发现，如果我们把同一层的点存起来，那么，先进先出的话，同层点在被访问过后，才会接着访问下一层的点。而先进先出正是队列的特点，所以，我们可以使用队列来实现BFS。

2.例题分析

https://vjudge.net/problem/HDU-1548

奇怪的电梯，可以使用BFS来解决，当然也可以使用DFS和Dijkstra

来解决（有兴趣可以尝试下）

奇怪的电梯题目输入是当前所在楼层，目的楼层，楼层总数，每层电梯只能上下的层数。

输出是最少的次数，不能到达则-1。

#include <queue>
#include <iostream>
#include <cstring>
using namespace std;
queue <int> q;
int num,s,e;
int a[1000];
int step[1000];
void bfs(){
    int m,n;
    while(!q.empty())
    {
        m = q.front();//取出当前队列第一个数，即当前楼层
        q.pop();
        n = m + a[m];//往上移动到的楼层数
        if(n >= 1 && n <= num && step[n] == -1)
        {
            step[n] = step[m] + 1;//步数自增
            q.push(n);//把当前（移动后的）楼层数加入队列
        }
        n = m - a[m];//往下移动到的楼层数
        if(n >= 1 && n <= num && step[n] == -1)
        {
            step[n] = step[m] + 1;//步数自增
            q.push(n);//把当前（移动后的）楼层数加入队列
        }
    }
    //队列为空，则表示没有可以移动的位置了，即所有能走的楼层均走过
    cout << step[e] << endl;
}
int main(){
    while(scanf("%d",&num)!= EOF)
    {
        if(num == 0)
        {
            break;
        }
        scanf("%d%d",&s,&e);//开始结束楼层
        for(int i = 1 ; i <= num ; i++)
        {
            scanf("%d",&a[i]);//每层固定上下移动的层数
        }
        memset(step,-1,sizeof(step));
        step[s] = 0;
        q.push(s);//将开始层数加入队列
        bfs();
    }
    return 0;
}

BFS对于求无权路的最短路径很方便，遍历一遍，到了对应的节点，则可以说是最短路径，对于有权图可以采用Dijkstra等等。

三.总结

BFS和DFS主要是一种遍历图的方式，理解透彻具体是什么，该怎么遍历，熟练之后便可以很快上手，那么该怎么熟练呢？当然是理解+刷题（笑。再来推荐道题目Serial Time! ，DFS，BFS都可以尝试下（逃