[HAOI2011]Problem c

题目描述

给n个人安排座位，先给每个人一个1~n的编号，设第i个人的编号为ai（不同人的编号可以相同），接着从第一个人开始，大家依次入座，第i个人来 了以后尝试坐到ai，如果ai被占据了，就尝试ai+1，ai+1也被占据了的话就尝试ai+2，……，如果一直尝试到第n个都不行，该安排方案就不合 法。然而有m个人的编号已经确定(他们或许贿赂了你的上司...)，你只能安排剩下的人的编号，求有多少种合法的安排方案。由于答案可能很大，只需输出其 除以M后的余数即可。

输入输出格式

输入格式：

第一行一个整数T，表示数据组数

对于每组数据，第一行有三个整数，分别表示n、m、M

若m不为0，则接下来一行有m对整数，p1、q1，p2、q2 ,…, pm、qm，其中第i对整数pi、qi表示第pi个人的编号必须为qi

输出格式：

对于每组数据输出一行，若是有解则输出YES，后跟一个整数表示方案数mod M，注意，YES和数之间只有一个空格，否则输出NO

输入输出样例

输入样例#1：

2
4 3 10
1 2 2 1 3 1
10 3 8882
7 9 2 9 5 10

输出样例#1：

YES 4
NO

说明

100%的数据满足：1≤T≤10，1≤n≤300，0≤m≤n，2≤M≤109，1≤pi、qi≤n 且保证pi互不相同。

首先，每个人都要有位置

那么意味着位置不能有空

也就是说，对于位置i，位置在i及i前面的人要大于i个，否则就填不满

每个i都符合条件则为合法

我们设sum[i]为可以填在1～i的人数

cnt[i]为必须填i的人数

显然sum可以通过cnt算出，具体方法:

sum[0]=n-m,sum[i]=sum[i-1]+cnt[i]

原因sum[i]肯定有∑cnt[1~i]然后算上不确定的n-m个人

这样就可以用sum[i]<i判断无解

求方案数用dp

令f[i][j]表示前i位，放j个人

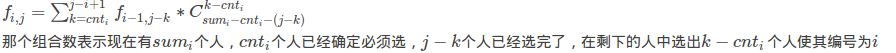
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 ll f[][],cnt[],sum[],C[][],Mod,n,m;
 int main()
 {int T,i,j,p,q,flag,k;
   cin>>T;
   while (T--)
     {
       cin>>n>>m>>Mod;
       memset(C,,sizeof(C));
       memset(cnt,,sizeof(cnt));
       memset(f,,sizeof(f));
       C[][]=;
       for (i=;i<=;i++)
     {C[i][]=;
       for (j=;j<=i;j++)
         C[i][j]=C[i-][j]+C[i-][j-],C[i][j]%=Mod;
     }
       for (i=;i<=m;i++)
     {
       scanf("%d%d",&p,&q);
       cnt[q]++;
     }
       sum[]=n-m;flag=;
       for (i=;i<=n;i++)
     {
       sum[i]=sum[i-]+cnt[i];
       if (sum[i]<i)
         {
           cout<<"NO\n";
           flag=;break;
         }
     }
       if (flag)
     {
       f[][]=;
       for (i=;i<=n;i++)
         {
           for (j=i;j<=sum[i];j++)
         {
           for (k=cnt[i];k<=j-i+;k++)
             {
               f[i][j]+=f[i-][j-k]*C[sum[i-]-(j-k)][k-cnt[i]]%Mod;
               f[i][j]%=Mod;
             }
         }
         }
       cout<<"YES "<<f[n][n]<<endl;
     }
     }
 }