string （KMP+期望DP）

Time Limit: 1000 ms   Memory Limit: 256 MB

Description

　　 给定一个由且仅由字符 'H' , 'T' 构成的字符串$S$.

　　给定一个最初为空的字符串$T$ , 每次随机地在$T$的末尾添加 'H' 或者 'T' .

　　问当$S$为$T$的后缀时, 在末尾添加字符的期望次数.

Input

　　输入只有一行, 一个字符串$S$.

Output

　　输出只有一行, 一个数表示答案.

　　为了防止运算越界, 你只用将答案对$10^9+7$取模.

Sample Input	Sample Output
HTHT	20

---

题解

　　 题目的本质其实就是：从左到右一位一位填字符（0或1，概率都为$0.5$），如果当前字符不满足目标串的相应字符，就要退回到之前的某一位继续匹配，求成功填满整个字符串的期望填充次数。

　　 其中，“退回”的操作，实际上是为了满足题目所说的“后缀”，这点要清楚，失配后不会从头开始，而是从类似KMP的next位置继续匹配。

　

支持数组：

　　那么我们对$S$预处理正常KMP的next数组，和一个数组$g[i][j]$ $(j=0,1)$，表示已正确填好前$i$位字符，第$i+1$位字符填了$j$后，匹配的位置。

　　设第$i+1$位正确的字符为$x$，那么有

　    $g[i][x]=i+1$

　　 $g[i][x\text^1]=g[next[i]][x\text^1]$

　　  如果当前第$i$位我们填入$y$，那么下一步我们就应该从$g[i-1][y]$处开始匹配。

　　

期望DP：

　　设$f_i$表示当前前$i$位已正确填充好，成功填入下一位$i+1$的期望填充次数，$wrong$为$i+1$位的错误字符。

　　转移即为：

　　

　　$\begin{aligned}
　　f_i&=0.5*1+0.5*(1+\sum_{j=g[i][wrong]}^{i}f_j)\\
　　f_i&=0.5*1+0.5*(1+f_i+\sum_{j=g[i][wrong]}^{i-1}f_j)\\
　　\frac{1}{2}f_i&=0.5*1+0.5*(1+\sum_{j=g[i][wrong]}^{i-1}f_j)\\
　　f_i&=2+\sum_{j=g[i][wrong]}^{i-1}f_j
　　\end{aligned}$

　　第一行什么意思呢？

　　我们有$0.5$的概率$1$次填上对的字符；

　　也有$0.5$的概率填充$1$次，结果填错了，蹦回$g[i][wrong]$，再一路走到$i+1$。

　　

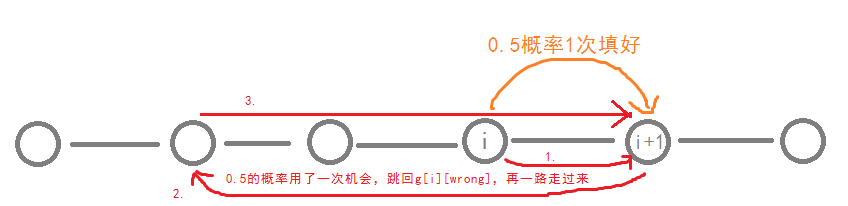
　　我们边算期望边处理一个前缀和$sum_i=\sum\limits_{j=0}^{i-1}f_j$，这样公式中求和的部分就变成了：

　　$f_i=2+sum_{i}-sum_{g[i][wrong]}$

　　答案也就是$sum_{len(S)}$，从$0$一路走到$S$的最后。

　　时空复杂度$O(n)$

---

 #include <cstdio>
 #include <cstring>
 using namespace std;
 typedef long long ll;
 const int N=,Mod=1e9+;
 char inp[N];
 int n,s[N],g[N][],nex[N];
 ll sum[N];
 ll max(ll x,ll y){return x>y?x:y;}
 void kmp(){
     nex[]=;
     for(int i=,j;i<=n;i++){
         j=nex[i-];
         while(j&&s[j+]!=s[i]) j=nex[j];
         if(s[j+]==s[i]) nex[i]=j+;
         else nex[i]=;
     }
     for(int i=;i<n;i++){
         g[i][s[i+]]=i+;
         g[i][s[i+]^]=g[nex[i]][s[i+]^];
     }
 }
 int main(){
     scanf("%s",inp+);
     n=strlen(inp+);
     for(int i=;i<=n;i++) s[i]=inp[i]=='T';
     kmp();
     ll f;
     sum[]=;
     for(int i=;i<n;i++){
         f=(sum[i]+Mod-sum[g[i][s[i+]^]]+)%Mod;
         sum[i+]=(sum[i]+f)%Mod;
     }
     printf("%lld\n",sum[n]);
     return ;
 }

奇妙代码