二维RMQ模板

int main(){
    for (int i = ; i <= n; i++)
        for (int j = ; j <= m; j++) {
            scanf("%d", &val[i][j]);
            dp[i][j][][] = val[i][j];
        }
 
    for (int i = ; ( << i) <= n; i++) {
        for (int j = ; ( << j) <= m; j++) {
            if (i ==  && j == ) continue;
            for (int row = ; row + ( << i) -  <= n; row++)
                for (int col = ; col + ( << j) -  <= m; col++) {
                    //当x或y等于0的时候，就相当于一维的RMQ了
                    //if(i == 0) dp[row][col][i][j] = max(dp[row][col][i][j - 1], dp[row][col + (1 << (j - 1))][i][j - 1]);
                    if (j == ) dp[row][col][i][j] = max(dp[row][col][i - ][j], dp[row + ( << (i - ))][col][i - ][j]);
                    else dp[row][col][i][j] = max(dp[row][col][i][j - ], dp[row][col + ( << (j - ))][i][j - ]);
                }
        }
    }
}

因为i == 0时的代码和 i != 0 && j != 0时的一样 所以就合并了

i  !=0 && j != 0时

查询：

询问的话，也要稍加改变，一维RMQ返回的是一段区间的最值，而二维的RMQ需要返回的一个矩阵的最值，所以返回的时候要注意，所返回的一定要构成一个矩阵

按照一维RMQ的思路来做的话，二维的就要返回四个值的最值了（假设询问的是(x1, y1), (x2, y2)这个矩阵内的最值） 
那么应该返回的是 
m1 = dp[x1][y1][k1][k2] 
m2 = dp[x2 - (1 << k1 ) + 1][y1][k1][k2] 
m3 = dp[x1][y2 - (1 << k2) + 1][k1][k2] 
m4 = dp[x2 - (1 << k1) + 1][y2 - (1 << k2) + 1][k1][k2] 
这四个值再去最值即可

//本来一维RMQ询问的时候是一个区间，现在变成了一个矩形，所以需要四个角度
int rmq(int x1, int y1, int x2, int y2) {
    int kx = , ky = ;
    while (( << ( + kx)) <= x2 - x1 + 1) kx++;
    while (( << ( + ky)) <= y2 - y1 + 1) ky++;
    int m1 = dp[x1][y1][kx][ky];
    int m2 = dp[x2 - ( << kx) + ][y1][kx][ky];
    int m3 = dp[x1][y2 - ( << ky) + ][kx][ky];
    int m4 = dp[x2 - ( << kx) + ][y2 - ( << ky) + ][kx][ky];
 
    return max(max(m1, m2), max(m3, m4));
}

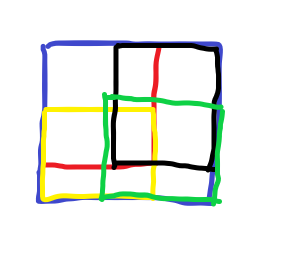
大约就是这样。。。手残 见谅。。

以上模板是求最大值  求最小值 该max为min即可