poj1673 EXOCENTER OF A TRIANGLE

地址：http://poj.org/problem?id=1673

题目：

EXOCENTER OF A TRIANGLE

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3637		Accepted: 1467

Description

Given a triangle ABC, the Extriangles of ABC are constructed as follows: 
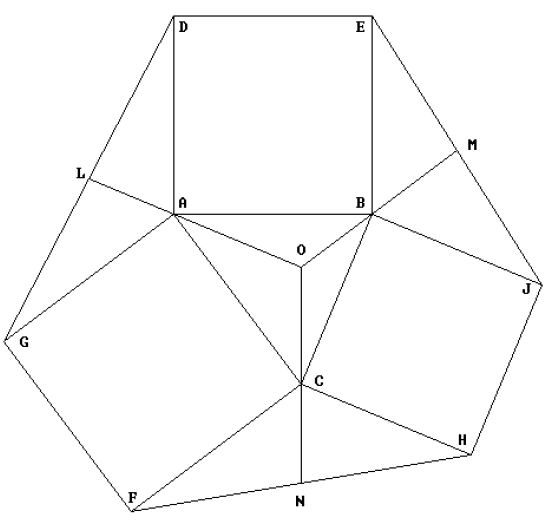
On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below). 
Connect adjacent square corners to form the three Extriangles (AGD, BEJ and CFH in the figure). 
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure). 
This problem is to write a program to compute the Exocenters of triangles. 

Input

The first line of the input consists of a positive integer n, which is the number of datasets that follow. Each dataset consists of 3 lines; each line contains two floating point values which represent the (two -dimensional) coordinate of one vertex of a triangle. So, there are total of (n*3) + 1 lines of input. Note: All input triangles wi ll be strongly non-degenerate in that no vertex will be within one unit of the line through the other two vertices.

Output

For each dataset you must print out the coordinates of the Exocenter of the input triangle correct to four decimal places.

Sample Input

2
0.0 0.0
9.0 12.0
14.0 0.0
3.0 4.0
13.0 19.0
2.0 -10.0

Sample Output

9.0000 3.7500
-48.0400 23.3600

Source

Greater New York 2003

 

思路：

　　其实就是重心。

 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <algorithm>

 using namespace std;
 const double PI = acos(-1.0);
 const double eps = 1e-;

 /****************常用函数***************/
 //判断ta与tb的大小关系
 int sgn( double ta, double tb)
 {
     if(fabs(ta-tb)<eps)return ;
     if(ta<tb)   return -;
     return ;
 }

 //点
 class Point
 {
 public:

     double x, y;

     Point(){}
     Point( double tx, double ty){ x = tx, y = ty;}

     bool operator < (const Point &_se) const
     {
         return x<_se.x || (x==_se.x && y<_se.y);
     }
     friend Point operator + (const Point &_st,const Point &_se)
     {
         return Point(_st.x + _se.x, _st.y + _se.y);
     }
     friend Point operator - (const Point &_st,const Point &_se)
     {
         return Point(_st.x - _se.x, _st.y - _se.y);
     }
     //点位置相同(double类型)
     bool operator == (const Point &_off)const
     {
         return  sgn(x, _off.x) ==  && sgn(y, _off.y) == ;
     }

 };

 /****************常用函数***************/
 //点乘
 double dot(const Point &po,const Point &ps,const Point &pe)
 {
     return (ps.x - po.x) * (pe.x - po.x) + (ps.y - po.y) * (pe.y - po.y);
 }
 //叉乘
 double xmult(const Point &po,const Point &ps,const Point &pe)
 {
     return (ps.x - po.x) * (pe.y - po.y) - (pe.x - po.x) * (ps.y - po.y);
 }
 //两点间距离的平方
 double getdis2(const Point &st,const Point &se)
 {
     return (st.x - se.x) * (st.x - se.x) + (st.y - se.y) * (st.y - se.y);
 }
 //两点间距离
 double getdis(const Point &st,const Point &se)
 {
     return sqrt((st.x - se.x) * (st.x - se.x) + (st.y - se.y) * (st.y - se.y));
 }

 //两点表示的向量
 class Line
 {
 public:

     Point s, e;//两点表示，起点[s]，终点[e]
     double a, b, c;//一般式,ax+by+c=0
     double angle;//向量的角度，[-pi,pi]

     Line(){}
     Line( Point ts, Point te):s(ts),e(te){}//get_angle();}
     Line(double _a,double _b,double _c):a(_a),b(_b),c(_c){}

     //排序用
     bool operator < (const Line &ta)const
     {
         return angle<ta.angle;
     }
     //向量与向量的叉乘
     friend double operator / ( const Line &_st, const  Line &_se)
     {
         return (_st.e.x - _st.s.x) * (_se.e.y - _se.s.y) - (_st.e.y - _st.s.y) * (_se.e.x - _se.s.x);
     }
     //向量间的点乘
     friend double operator *( const Line &_st, const  Line &_se)
     {
         return (_st.e.x - _st.s.x) * (_se.e.x - _se.s.x) - (_st.e.y - _st.s.y) * (_se.e.y - _se.s.y);
     }
     //从两点表示转换为一般表示
     //a=y2-y1,b=x1-x2,c=x2*y1-x1*y2
     bool pton()
     {
         a = e.y - s.y;
         b = s.x - e.x;
         c = e.x * s.y - e.y * s.x;
         return true;
     }
     //半平面交用
     //点在向量左边（右边的小于号改成大于号即可,在对应直线上则加上=号）
     friend bool operator < (const Point &_Off, const Line &_Ori)
     {
         return (_Ori.e.y - _Ori.s.y) * (_Off.x - _Ori.s.x)
             < (_Off.y - _Ori.s.y) * (_Ori.e.x - _Ori.s.x);
     }
     //求直线或向量的角度
     double get_angle( bool isVector = true)
     {
         angle = atan2( e.y - s.y, e.x - s.x);
         if(!isVector && angle < )
             angle += PI;
         return angle;
     }

     //点在线段或直线上 1:点在直线上 2点在s,e所在矩形内
     bool has(const Point &_Off, bool isSegment = false) const
     {
         bool ff = sgn( xmult( s, e, _Off), ) == ;
         if( !isSegment) return ff;
         return ff
             && sgn(_Off.x - min(s.x, e.x), ) >=  && sgn(_Off.x - max(s.x, e.x), ) <=
             && sgn(_Off.y - min(s.y, e.y), ) >=  && sgn(_Off.y - max(s.y, e.y), ) <= ;
     }

     //点到直线/线段的距离
     double dis(const Point &_Off, bool isSegment = false)
     {
         ///化为一般式
         pton();
         //到直线垂足的距离
         double td = (a * _Off.x + b * _Off.y + c) / sqrt(a * a + b * b);
         //如果是线段判断垂足
         if(isSegment)
         {
             double xp = (b * b * _Off.x - a * b * _Off.y - a * c) / ( a * a + b * b);
             double yp = (-a * b * _Off.x + a * a * _Off.y - b * c) / (a * a + b * b);
             double xb = max(s.x, e.x);
             double yb = max(s.y, e.y);
             double xs = s.x + e.x - xb;
             double ys = s.y + e.y - yb;
            if(xp > xb + eps || xp < xs - eps || yp > yb + eps || yp < ys - eps)
                 td = min( getdis(_Off,s), getdis(_Off,e));
         }
         return fabs(td);
     }

     //关于直线对称的点
     Point mirror(const Point &_Off)
     {
         ///注意先转为一般式
         Point ret;
         double d = a * a + b * b;
         ret.x = (b * b * _Off.x - a * a * _Off.x -  * a * b * _Off.y -  * a * c) / d;
         ret.y = (a * a * _Off.y - b * b * _Off.y -  * a * b * _Off.x -  * b * c) / d;
         return ret;
     }
     //计算两点的中垂线
     static Line ppline(const Point &_a,const Point &_b)
     {
         Line ret;
         ret.s.x = (_a.x + _b.x) / ;
         ret.s.y = (_a.y + _b.y) / ;
         //一般式
         ret.a = _b.x - _a.x;
         ret.b = _b.y - _a.y;
         ret.c = (_a.y - _b.y) * ret.s.y + (_a.x - _b.x) * ret.s.x;
         //两点式
         if(fabs(ret.a) > eps)
         {
             ret.e.y = 0.0;
             ret.e.x = - ret.c / ret.a;
             if(ret.e == ret. s)
             {
                 ret.e.y = 1e10;
                 ret.e.x = - (ret.c - ret.b * ret.e.y) / ret.a;
             }
         }
         else
         {
             ret.e.x = 0.0;
             ret.e.y = - ret.c / ret.b;
             if(ret.e == ret. s)
             {
                 ret.e.x = 1e10;
                 ret.e.y = - (ret.c - ret.a * ret.e.x) / ret.b;
             }
         }
         return ret;
     }

     //------------直线和直线（向量）-------------
     //向量向左边平移t的距离
     Line& moveLine( double t)
     {
         Point of;
         of = Point( -( e.y - s.y), e.x - s.x);
         double dis = sqrt( of.x * of.x + of.y * of.y);
         of.x= of.x * t / dis, of.y = of.y * t / dis;
         s = s + of, e = e + of;
         return *this;
     }
     //直线重合
     static bool equal(const Line &_st,const Line &_se)
     {
         return _st.has( _se.e) && _se.has( _st.s);
     }
     //直线平行
     static bool parallel(const Line &_st,const Line &_se)
     {
         return sgn( _st / _se, ) == ;
     }
     //两直线（线段）交点
     //返回-1代表平行，0代表重合，1代表相交
     static bool crossLPt(const Line &_st,const Line &_se, Point &ret)
     {
         if(parallel(_st,_se))
         {
             if(Line::equal(_st,_se)) return ;
             return -;
         }
         ret = _st.s;
         double t = ( Line(_st.s,_se.s) / _se) / ( _st / _se);
         ret.x += (_st.e.x - _st.s.x) * t;
         ret.y += (_st.e.y - _st.s.y) * t;
         return ;
     }
     //------------线段和直线（向量）----------
     //直线和线段相交
     //参数：直线[_st],线段[_se]
     friend bool crossSL( Line &_st, Line &_se)
     {
         return sgn( xmult( _st.s, _se.s, _st.e) * xmult( _st.s, _st.e, _se.e), ) >= ;
     }

     //判断线段是否相交(注意添加eps)
     static bool isCrossSS( const Line &_st, const  Line &_se)
     {
         //1.快速排斥试验判断以两条线段为对角线的两个矩形是否相交
         //2.跨立试验（等于0时端点重合）
         return
             max(_st.s.x, _st.e.x) >= min(_se.s.x, _se.e.x) &&
             max(_se.s.x, _se.e.x) >= min(_st.s.x, _st.e.x) &&
             max(_st.s.y, _st.e.y) >= min(_se.s.y, _se.e.y) &&
             max(_se.s.y, _se.e.y) >= min(_st.s.y, _st.e.y) &&
             sgn( xmult( _se.s, _st.s, _se.e) * xmult( _se.s, _se.e, _st.s), ) >=  &&
             sgn( xmult( _st.s, _se.s, _st.e) * xmult( _st.s, _st.e, _se.s), ) >= ;
     }
 };

 //寻找凸包的graham 扫描法所需的排序函数
 Point gsort;
 bool gcmp( const Point &ta, const Point &tb)/// 选取与最后一条确定边夹角最小的点，即余弦值最大者
 {
     double tmp = xmult( gsort, ta, tb);
     if( fabs( tmp) < eps)
         return getdis( gsort, ta) < getdis( gsort, tb);
     else if( tmp > )
         return ;
     return ;
 }

 class triangle
 {
 public:
     Point a, b, c;//顶点
     triangle(){}
     triangle(Point a, Point b, Point c): a(a), b(b), c(c){}

     //计算三角形面积
     double area()
     {
         return fabs( xmult(a, b, c)) / 2.0;
     }

     //计算三角形外心
     //返回：外接圆圆心
     Point circumcenter()
     {
         double pa = a.x * a.x + a.y * a.y;
         double pb = b.x * b.x + b.y * b.y;
         double pc = c.x * c.x + c.y * c.y;
         double ta = pa * ( b.y - c.y) - pb * ( a.y - c.y) + pc * ( a.y - b.y);
         double tb = -pa * ( b.x - c.x) + pb * ( a.x - c.x) - pc * ( a.x - b.x);
         double tc = a.x * ( b.y - c.y) - b.x * ( a.y - c.y) + c.x * ( a.y - b.y);
         return Point( ta / 2.0 / tc, tb / 2.0 / tc);
     }

     //计算三角形内心
     //返回：内接圆圆心
     Point incenter()
     {
         Line u, v;
         double m, n;
         u.s = a;
         m = atan2(b.y - a.y, b.x - a.x);
         n = atan2(c.y - a.y, c.x - a.x);
         u.e.x = u.s.x + cos((m + n) / );
         u.e.y = u.s.y + sin((m + n) / );
         v.s = b;
         m = atan2(a.y - b.y, a.x - b.x);
         n = atan2(c.y - b.y, c.x - b.x);
         v.e.x = v.s.x + cos((m + n) / );
         v.e.y = v.s.y + sin((m + n) / );
         Point ret;
         Line::crossLPt(u,v,ret);
         return ret;
     }

     //计算三角形垂心
     //返回：高的交点
     Point perpencenter()
     {
         Line u,v;
         u.s = c;
         u.e.x = u.s.x - a.y + b.y;
         u.e.y = u.s.y + a.x - b.x;
         v.s = b;
         v.e.x = v.s.x - a.y + c.y;
         v.e.y = v.s.y + a.x - c.x;
         Point ret;
         Line::crossLPt(u,v,ret);
         return ret;
     }

     //计算三角形重心
     //返回：重心
     //到三角形三顶点距离的平方和最小的点
     //三角形内到三边距离之积最大的点
     Point barycenter()
     {
         Line u,v;
         u.s.x = (a.x + b.x) / ;
         u.s.y = (a.y + b.y) / ;
         u.e = c;
         v.s.x = (a.x + c.x) / ;
         v.s.y = (a.y + c.y) / ;
         v.e = b;
         Point ret;
         Line::crossLPt(u,v,ret);
         return ret;
     }

     //计算三角形费马点
     //返回：到三角形三顶点距离之和最小的点
     Point fermentPoint()
     {
         Point u, v;
         double step = fabs(a.x) + fabs(a.y) + fabs(b.x) + fabs(b.y) + fabs(c.x) + fabs(c.y);
         int i, j, k;
         u.x = (a.x + b.x + c.x) / ;
         u.y = (a.y + b.y + c.y) / ;
         while (step > eps)
         {
             for (k = ; k < ; step /= , k ++)
             {
                 for (i = -; i <= ; i ++)
                 {
                     for (j =- ; j <= ; j ++)
                     {
                         v.x = u.x + step * i;
                         v.y = u.y + step * j;
                         if (getdis(u,a) + getdis(u,b) + getdis(u,c) > getdis(v,a) + getdis(v,b) + getdis(v,c))
                             u = v;
                     }
                 }
             }
         }
         return u;
     }
 };

 triangle tr;
 int main(void)
 {
     int n;
     scanf("%d",&n);
     while(n--)
     {
         scanf("%lf%lf%lf%lf%lf%lf",&tr.a.x,&tr.a.y,&tr.b.x,&tr.b.y,&tr.c.x,&tr.c.y);
         Point ans=tr.perpencenter();
         printf("%.4f %.4f\n",ans.x,ans.y);
     }
     return ;
 }