HDU-5226 Tom and matrix(组合数求模)

一、题目链接

　　http://acm.hdu.edu.cn/showproblem.php?pid=5226

二、题意

　　给一个大矩阵，其中，$a[i][j] = C_i^j$。输入5个参数，$x_1, y_1, x_2, y_2, p$，输出：以$x_1, y_1$为左上角，$x_2, y_2$为右下角的子矩阵中所有值累加和$\% p$的结果。

三、思路

　　看完题意后，想了一会儿，实在想不到如何降低复杂度。于是，就去看题解了。(PS:想了大概20分钟左右后还是没思路可以果断去看题解了。既然不知道方法，想再久也没用，最后还是要看题解的)。所以，我这篇文章，只是对知识点的整理和总结，而不是原创思路的分享。

　　对于组合数来说，有$C_n^m = C_{n-1}^{m-1} + C_{n-1}^m$。看个表。

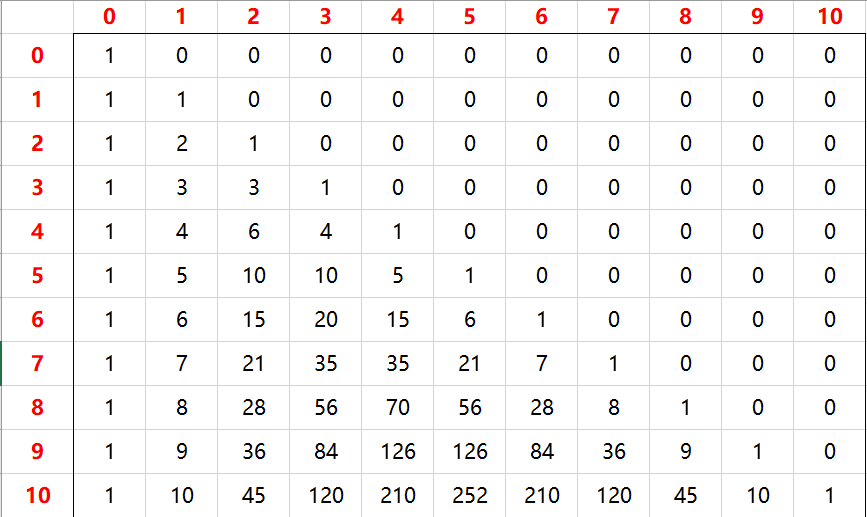
　　这个表大家都很熟悉，就是组合数的表，因为$C_n^m = C_{n-1}^{m-1} + C_{n-1}^m$，所以，\[C_{n+1}^m = C_n^{m-1} + C_n^m = C_n^{m-1} + C_{n-1}^{m-1} + C_{n-1}^m = C_n^{m-1} + C_{n-1}^{m-1} + C_{n-2}^{m-1}+C_{n-2}^{m}\]，由上述递推式可以发现，要计算$\sum\limits_{i=x_1}^{x_2}a[i][y]$，只要计算$C_{x_2+1}^{y+1} - C_{x_1}^{y+1}$即可。而且，更巧的是，对于对角线上的值，该式子也成立。

　　那么，有了上述推论，复杂度就降了一个维度了。从$y_1$枚举每一列到$y_2$，对每一列使用上述公式求值即可。

　　在做组合数求模$C_n^m\ \%\ p$的过程中，因为有可能存在$p \le \frac{n}{m}$的样例，那么就会出现这么一种情况：$p | n!, p | m!, p | (n-m)!$，如果使用n的阶乘*m的阶乘的逆元*(n-m)的阶乘的逆元来计算，返回值会是0。而实际上，真正的返回值并不一定是0。举个例子：

\[C_6^2 = \frac{6!}{2! * 4!} = \frac{720}{2 * 24} = 15\]

\[C_6^2\ \%\ 2 = 15\ \%\ 2 = 1 \ne 0 \]

　　所以，直接做计算组合数求模是不行的(也就是说，如果存在上述情况，用扩展欧几里得算法、费马小定理算法都不行了)，要用lucas定理才行。

　　另外，还要注意的一点是，在初始化阶乘数组的时候，千万别忘了初始化阶乘逆元数组的第0个元素。即：inv[0] = 1。

四、源代码

　　

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100100
using namespace std;
typedef long long LL;
LL facts[MAXN], inv0[MAXN], x1, x2, y1, y2, p;

LL qpow(LL a, LL x) {
    LL res = ;
    ) {
        )res = (res * a) % p;
        a = (a * a) % p;
        x >>= ;
    }
    return res;
}

void init() {
    facts[] = inv0[] = ;
    ; i < MAXN; ++i) {
        facts[i] = (facts[i - ] * i) % p;
        inv0[i] = qpow(facts[i], p - );
    }
}

LL C(LL n, LL m) {
    ;
    );
    )return n % p;
    return facts[n] * inv0[m] % p * inv0[n - m] % p;
}

LL lucas(LL n, LL m) {
    if(n < p && m < p)return C(n, m);
    else return lucas(n / p, m / p) * lucas(n % p, m % p) % p;
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("input.txt", "r", stdin);
#endif
    while(~scanf("%I64d %I64d %I64d %I64d %I64d", &x1, &y1, &x2, &y2, &p)) {
        init();
        LL ans = ;
        ;i <= y2 + ;++i)ans = (ans + lucas(x2 + , i) - lucas(x1, i) + p) % p;
        printf("%I64d\n", ans);
    }
    ;
}