【POJ-1390】Blocks 区间DP

Blocks

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 5252		Accepted: 2165

Description

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold. 
The corresponding picture will be as shown below: 
 
Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.

Now let's look at the picture below: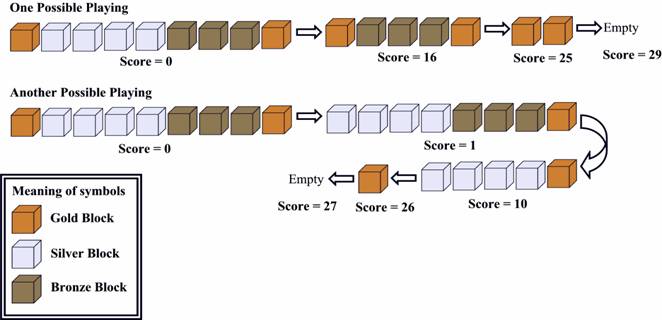 
 
Figure 2

The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

Input

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.

Output

For each test case, print the case number and the highest possible score.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1

Source

Liu Rujia@POJ

Solution

lrj出的题好劲啊......写的TA爷的做法

一个比较厉害的状态$f[l][r][k]$表示当$a[l]==a[r]$时，将$l~r$这个整段玩到还剩连续的$k$个$a[l]/a[r]$色的块时得到的最大的值。

但是单靠这个是不足以转移的，

另一个状态$g[l][r]$表示，不管以什么方法，删光$l~r$这段的得到的最大的值。

然后进行区间DP，显然要枚举区间，枚举断点，转移就是；

$$f[l][r][k]=max(f[l][r][k],f[l][r][k-1]+g[k'-1][r-1]);$$

这个转移就是把区间$l~r$中花式删掉$k'~r-1$这段，剩下的组成$k$个的最大方案。

$$g[l][r]=max(g[l][r],f[l][r][k]+k*k,g[l][k']+g[k'+1][r]);$$

这个转移比较显然..

然后这样转移之后，显然$f[l][r][0]=g[l][r]$.

答案就是$f[1][N][0]/g[1][N]$，时间复杂度是$<=O(N^4)$的，而且在正常的数据下表现非常优秀。

Code

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
inline int read()
{
    int x=,f=; char ch=getchar();
    while (ch<'' || ch>'') {if (ch=='-') f=-; ch=getchar();}
    while (ch>='' && ch<='') {x=x*+ch-''; ch=getchar();}
    return x*f;
}
int T,N,a[],f[][][],g[][],t,cnt[][];
int main()
{
    T=read();
    while (T--)
        {
            N=read();
            for (int i=; i<=N; i++) a[i]=read();
            memset(cnt,,sizeof(cnt));
            for (int i=; i<=N; i++)
                for (int j=i+; j<=N; j++)
                    if (a[i]==a[j])
                        for (int k=i; k<=j; k++)
                            if (a[k]==a[i]) cnt[i][j]++;
            memset(f,,sizeof(f)); memset(g,,sizeof(g));
            for (int i=; i<=N; i++) g[i][i]=f[i][i][]=,f[i][i][]=;
            for (int len=; len<=N; len++)
                for (int l=; l+len-<=N; l++)
                    {
                        int r=l+len-;
                        for (int i=; i<=cnt[l][r]; i++)
                            {
                                for (int j=l; j<r; j++)
                                    f[l][r][i]=max(f[l][r][i],f[l][j][i-]+g[j+][r-]);
                                g[l][r]=max(g[l][r],f[l][r][i]+i*i);
                            }
                        for (int i=l; i<r; i++) g[l][r]=max(g[l][r],g[l][i]+g[i+][r]);
                        f[l][r][]=g[l][r];
                    }
            printf("Case %d: %d\n",++t,f[][N][]);
        }
    return ;
}