八大排序算法——基数排序（动图演示 思路分析 实例代码java 复杂度分析）

一、动图演

二、思路分析

基数排序第i趟将待排数组里的每个数的i位数放到tempj（j=1-10）队列中，然后再从这十个队列中取出数据，重新放到原数组里，直到i大于待排数的最大位数。

1.数组里的数最大位数是n位，就需要排n趟，例如数组里最大的数是3位数，则需要排3趟。

2.若数组里共有m个数，则需要十个长度为m的数组tempj（j=0-9）用来暂存i位上数为j的数，例如，第1趟，各位数为0的会被分配到temp0数组里，各位数为1的会被分配到temp1数组里......

3.分配结束后，再依次从tempj数组中取出数据，遵循先进先进原则，例如对数组{1，11，2，44，4}，进行第1趟分配后，temp1={1,11}，temp2={2}，temp4={44，4}，依次取出元素后{1，11，2，44，4}，第一趟结束

4.循环到n趟后结束，排序完成

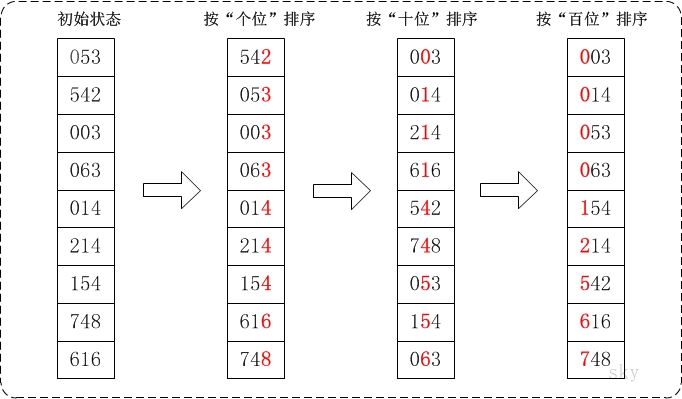
根据思路分析，每一趟的执行流程如下图所示：

通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}：

三、负杂度分析

1.  时间复杂度：

每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。

假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d*2n) ，当然d要远远小于n，因此基本上还是线性级别的。

系数2可以省略，且无论数组是否有序，都需要从个位排到最大位数，所以时间复杂度始终为O(d*n) 。其中，n是数组长度，d是最大位数。

2.  空间复杂度： 

　　基数排序的空间复杂度为O(n+k)，其中k为桶的数量，需要分配n个数。

 四、Java 代码如下

import java.util.Arrays;
public class Main {
    public static void main(String[] args) {
        int[] arr = new int[]{10,6,3,8,33,27,66,9,7,88};
        radixSort(arr);
    }

    private static void radixSort(int[] arr) {
        //求出待排数的最大数
        int maxLength=0;
        for (int i = 0; i < arr.length; i++) {
            if(maxLength<arr[i])
                maxLength = arr[i];
        }
        //根据最大数求最大长度
        maxLength = (maxLength+"").length();

        //用于暂存数据的数组
        int[][] temp = new int[10][arr.length];
        //用于记录temp数组中每个桶内存的数据的数量
        int[] counts = new int[10];
        //用于记录每个数的i位数
        int num = 0;
        //用于取的元素需要放的位置
        int index = 0;
        //根据最大长度决定排序的次数
        for (int i = 0,n=1; i < maxLength; i++,n*=10) {
            for (int j = 0; j < arr.length; j++) {
                num = arr[j]/n%10;
                temp[num][counts[num]] = arr[j];
                counts[num]++;
            }

            //从temp中取元素重新放到arr数组中
            for (int j = 0; j < counts.length; j++) {
                for (int j2 = 0; j2 < counts[j]; j2++) {
                    arr[index] = temp[j][j2];
                    index++;
                }
                counts[j]=0;
            }
            index=0;
        }
        System.out.println(Arrays.toString(arr));
    }
}