poj 1375

一道解析几何么，，，

其实就是求直线与圆的切线。

看到方法有很多，比如根据角度之类的。

这里主要用到了初中的几何知识。

考虑这幅图。

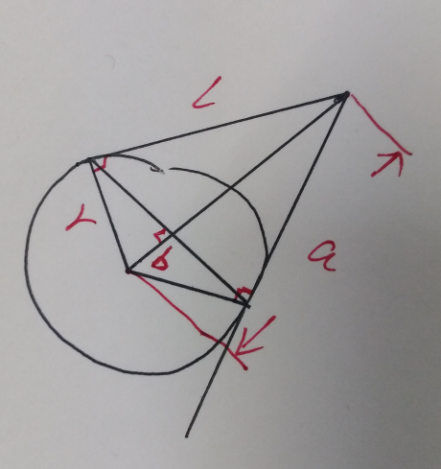
首先可以根据相似三角形知道b的长度，同时圆心与点的方向也知道。 那么 圆心+b 就是  切点连线 与 点与圆心 连线的交点了。

然后根据 面积，有 l·r = (b的长度)*(中间点到切点的长度) .

就很容易得到切点了。详细看代码，poj返回vector好像会RE，就改成pair了。

 #include <cstdio>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <map>
 #include <cstring>
 using namespace std;
 typedef double db;
 const db eps = 1e-;
 const db pi = acos(-);
 int sign(db k){
     if (k>eps) return ; else if (k<-eps) return -; return ;
 }
 int cmp(db k1,db k2){return sign(k1-k2);}
 struct point{
     db x,y;
     point operator + (const point &k1) const{return (point){k1.x+x,k1.y+y};}
     point operator - (const point &k1) const{return (point){x-k1.x,y-k1.y};}
     point operator * (db k1) const{return (point){x*k1,y*k1};}
     point operator / (db k1) const{return (point){x/k1,y/k1};}
     point turn(db k1){ return (point){x*cos(k1)-y*sin(k1),x*sin(k1)+y*cos(k1)};}
     point turn90(){ return (point){-y,x};}
     db abs(){ return sqrt(x*x+y*y);}
     db abs2(){ return x*x+y*y;}
     db dis(point k1){ return (*this-k1).abs();}
     point unit(){db w=abs(); return (point){x/w,y/w};}
 };
 db cross(point k1,point k2){ return k1.x*k2.y-k1.y*k2.x;}
 db dot(point k1,point k2){ return k1.x*k2.x+k1.y*k2.y;}
 point proj(point k1,point k2,point q){
     point k=k2-k1;
     return k1+k*(dot(q-k1,k)/k.abs2());
 }
 point getLL(point k1,point k2,point k3,point k4){
     db w1=cross(k1-k3,k4-k3),w2=cross(k4-k3,k2-k3);
     return (k1*w2+k2*w1)/(w1+w2);
 }
 struct circle{
     point o;db r;
     int inside(point k){ return cmp(r,o.dis(k));}
 };
 pair<point,point> TangentCP(circle k1,point k2){//
     db a=(k2-k1.o).abs(),b=k1.r*k1.r/a,c=sqrt(max((db)0.0,k1.r*k1.r-b*b));
     point k=(k2-k1.o).unit(),m=k1.o+k*b,del=k.turn90()*c;
     return {m-del,m+del};
 }
 struct line{
     db l,r;
 };
 bool cmp2(line a,line b){
     return a.l<b.l;
 }
 int n;
 line l[];
 circle c[];
 pair<point,point> g;
 point e,s1,s2;
 int main(){
     bool f=;
     while (scanf("%d",&n)&&n){
         if(f)printf("\n");
         f=;
         scanf("%lf%lf",&e.x,&e.y);
         for(int i=;i<=n;i++){
             scanf("%lf%lf%lf",&c[i].o.x,&c[i].o.y,&c[i].r);
         }
         for(int i=;i<=n;i++){
             g=TangentCP(c[i],e);
             s1 = getLL(e,g.first,point{0.0,0.0},point{100.0,0.0});
             s2 = getLL(e,g.second,point{0.0,0.0},point{100.0,0.0});
             l[i]=line{s2.x,s1.x};
         }
         sort(l+,l++n,cmp2);
         db L = l[].l,R = l[].r;
         for(int i=;i<=n;i++){
             if(l[i].l>R){
                 printf("%.2f %.2f\n",L,R);
                 L = l[i].l,R=l[i].r;
             } else
                 R = max(R,l[i].r);
         }
         printf("%.2f %.2f\n",L,R);
     }
 }
 /**
  *
 1
 300 300
 390 150 90
 0

 6
 300 450
 70 50 30
 120 20 20
 270 40 10
 250 85 20
 220 30 30
 380 100 100
  */