拓扑排序(三)之 Java详解

前面分别介绍了拓扑排序的C和C++实现，本文通过Java实现拓扑排序。

目录
1. 拓扑排序介绍
2. 拓扑排序的算法图解
3. 拓扑排序的代码说明
4. 拓扑排序的完整源码和测试程序

转载请注明出处：http://www.cnblogs.com/skywang12345/

更多内容：数据结构与算法系列 目录

拓扑排序介绍

拓扑排序(Topological Order)是指，将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。

这样说，可能理解起来比较抽象。下面通过简单的例子进行说明！
例如，一个项目包括A、B、C、D四个子部分来完成，并且A依赖于B和D，C依赖于D。现在要制定一个计划，写出A、B、C、D的执行顺序。这时，就可以利用到拓扑排序，它就是用来确定事物发生的顺序的。

在拓扑排序中，如果存在一条从顶点A到顶点B的路径，那么在排序结果中B出现在A的后面。

拓扑排序的算法图解

拓扑排序算法的基本步骤：

1. 构造一个队列Q(queue) 和 拓扑排序的结果队列T(topological)；
2. 把所有没有依赖顶点的节点放入Q；
3. 当Q还有顶点的时候，执行下面步骤：
3.1 从Q中取出一个顶点n(将n从Q中删掉)，并放入T(将n加入到结果集中)；
3.2 对n每一个邻接点m(n是起点，m是终点)；
3.2.1 去掉边<n,m>;
3.2.2 如果m没有依赖顶点，则把m放入Q;
注：顶点A没有依赖顶点，是指不存在以A为终点的边。

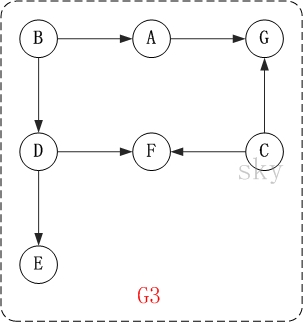
以上图为例，来对拓扑排序进行演示。

第1步：将B和C加入到排序结果中。
    顶点B和顶点C都是没有依赖顶点，因此将C和C加入到结果集T中。假设ABCDEFG按顺序存储，因此先访问B，再访问C。访问B之后，去掉边<B,A>和<B,D>，并将A和D加入到队列Q中。同样的，去掉边<C,F>和<C,G>，并将F和G加入到Q中。
    (01) 将B加入到排序结果中，然后去掉边<B,A>和<B,D>；此时，由于A和D没有依赖顶点，因此并将A和D加入到队列Q中。
    (02) 将C加入到排序结果中，然后去掉边<C,F>和<C,G>；此时，由于F有依赖顶点D，G有依赖顶点A，因此不对F和G进行处理。
第2步：将A,D依次加入到排序结果中。
    第1步访问之后，A,D都是没有依赖顶点的，根据存储顺序，先访问A，然后访问D。访问之后，删除顶点A和顶点D的出边。
第3步：将E,F,G依次加入到排序结果中。

因此访问顺序是：B -> C -> A -> D -> E -> F -> G

拓扑排序的代码说明

拓扑排序是对有向无向图的排序。下面以邻接表实现的有向图来对拓扑排序进行说明。

1. 基本定义

public class ListDG {
    // 邻接表中表对应的链表的顶点
    private class ENode {
        int ivex;       // 该边所指向的顶点的位置
        ENode nextEdge; // 指向下一条弧的指针
    }

    // 邻接表中表的顶点
    private class VNode {
        char data;          // 顶点信息
        ENode firstEdge;    // 指向第一条依附该顶点的弧
    };

    private VNode[] mVexs;  // 顶点数组

    ...
}

(01) ListDG是邻接表对应的结构体。 mVexs则是保存顶点信息的一维数组。
(02) VNode是邻接表顶点对应的结构体。 data是顶点所包含的数据，而firstEdge是该顶点所包含链表的表头指针。
(03) ENode是邻接表顶点所包含的链表的节点对应的结构体。 ivex是该节点所对应的顶点在vexs中的索引，而nextEdge是指向下一个节点的。

2. 拓扑排序

/*
 * 拓扑排序
 *
 * 返回值：
 *     -1 -- 失败(由于内存不足等原因导致)
 *      0 -- 成功排序，并输入结果
 *      1 -- 失败(该有向图是有环的)
 */
public int topologicalSort() {
    int index = 0;
    int num = mVexs.size();
    int[] ins;               // 入度数组
    char[] tops;             // 拓扑排序结果数组，记录每个节点的排序后的序号。
    Queue<Integer> queue;    // 辅组队列

    ins   = new int[num];
    tops  = new char[num];
    queue = new LinkedList<Integer>();

    // 统计每个顶点的入度数
    for(int i = 0; i < num; i++) {

        ENode node = mVexs.get(i).firstEdge;
        while (node != null) {
            ins[node.ivex]++;
            node = node.nextEdge;
        }
    }

    // 将所有入度为0的顶点入队列
    for(int i = 0; i < num; i ++)
        if(ins[i] == 0)
            queue.offer(i);                 // 入队列

    while (!queue.isEmpty()) {              // 队列非空
        int j = queue.poll().intValue();    // 出队列。j是顶点的序号
        tops[index++] = mVexs.get(j).data;  // 将该顶点添加到tops中，tops是排序结果
        ENode node = mVexs.get(j).firstEdge;// 获取以该顶点为起点的出边队列

        // 将与"node"关联的节点的入度减1；
        // 若减1之后，该节点的入度为0；则将该节点添加到队列中。
        while(node != null) {
            // 将节点(序号为node.ivex)的入度减1。
            ins[node.ivex]--;
            // 若节点的入度为0，则将其"入队列"
            if( ins[node.ivex] == 0)
                queue.offer(node.ivex);    // 入队列

            node = node.nextEdge;
        }
    }

    if(index != num) {
        System.out.printf("Graph has a cycle\n");
        return 1;
    }

    // 打印拓扑排序结果
    System.out.printf("== TopSort: ");
    for(int i = 0; i < num; i ++)
        System.out.printf("%c ", tops[i]);
    System.out.printf("\n");

    return 0;
}

说明：
(01) queue的作用就是用来存储没有依赖顶点的顶点。它与前面所说的Q相对应。
(02) tops的作用就是用来存储排序结果。它与前面所说的T相对应。

拓扑排序的完整源码和测试程序

拓扑排序源码(ListDG.java)