深度学习基础系列（一）| 一文看懂用kersa构建模型的各层含义（掌握输出尺寸和可训练参数数量的计算方法）

　　我们在学习成熟网络模型时，如VGG、Inception、Resnet等，往往面临的第一个问题便是这些模型的各层参数是如何设置的呢？另外，我们如果要设计自己的网路模型时，又该如何设置各层参数呢？如果模型参数设置出错的话，其实模型也往往不能运行了。

　　所以，我们需要首先了解模型各层的含义，比如输出尺寸和可训练参数数量。理解后，大家在设计自己的网路模型时，就可以先在纸上画出网络流程图，设置各参数，计算输出尺寸和可训练参数数量，最后就可以照此进行编码实现了。

　　而在keras中，当我们构建模型或拿到一个成熟模型后，往往可以通过model.summary()来观察模型各层的信息。

　　本文将通过一个简单的例子来进行说明。本例以keras官网的一个简单模型VGG-like模型为基础，稍加改动代码如下：

from tensorflow import keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Flatten
from tensorflow.keras.layers import Conv2D, MaxPool2D

(train_data, train_labels), (test_data, test_labels) = keras.datasets.mnist.load_data()
train_data = train_data.reshape(-1, 28, 28, 1)
print("train data type:{}, shape:{}, dim:{}".format(type(train_data), train_data.shape, train_data.ndim))

# 第一组
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(3, 3), strides=(1, 1), padding='valid', activation='relu', input_shape=(28, 28, 1)))
model.add(Conv2D(filters=32, kernel_size=(3, 3), strides=(1, 1), padding='valid', activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))

# 第二组
model.add(Conv2D(filters=64, kernel_size=(3, 3), strides=(1, 1), padding='valid', activation='relu'))
model.add(Conv2D(filters=64, kernel_size=(3, 3), strides=(1, 1), padding='valid', activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))

# 第三组
model.add(Flatten())
model.add(Dense(units=256, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=10, activation='softmax'))

model.summary()

　　本例的数据来源于mnist，这是尺寸为28*28，通道数为1，也即只有黑白两色的图片。其中卷积层的参数含义为：

• 　　filters：表示过滤器的数量，每一个过滤器都会与对应的输入层进行卷积操作；
• 　　kernel_size：表示过滤器的尺寸，一般为奇数值，如1,3,5，这里设置为3*3大小；
• 　　strides：表示步长，即每一次过滤器在图片上移动的步数；
• 　　padding：表示是否对图片边缘填充像素，一般有两个值可选，一是默认的valid，表示不填充像素，卷积后图片尺寸会变小；另一种是same，填充像素，使得输出尺寸和输入尺寸保持一致。

　　　　   如果选择valid，假设输入尺寸为n * n，过滤器的大小为f * f，步长为s，则其输出图片的尺寸公式为：[(n - f)/s + 1] * [(n -f)/s + 1)]，若计算结果不为整数，则向下取整；

　　　　  如果选择same，假设输入尺寸为n * n，过滤器的大小为f * f，要填充的边缘像素宽度为p，则计算p的公式为：n + 2p -f  +1 = n， 最后得 p = (f -1) /2。

　　运行上述例子，可以看到如下结果：

train data type:<class 'numpy.ndarray'>, shape:(60000, 28, 28, 1), dim:4
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
conv2d (Conv2D)              (None, 26, 26, 32)        320
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 24, 24, 32)        9248
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 12, 12, 32)        0
_________________________________________________________________
dropout (Dropout)            (None, 12, 12, 32)        0
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 10, 10, 64)        18496
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 8, 8, 64)          36928
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 4, 4, 64)          0
_________________________________________________________________
dropout_1 (Dropout)          (None, 4, 4, 64)          0
_________________________________________________________________
flatten (Flatten)            (None, 1024)              0
_________________________________________________________________
dense (Dense)                (None, 256)               262400
_________________________________________________________________
dropout_2 (Dropout)          (None, 256)               0
_________________________________________________________________
dense_1 (Dense)              (None, 10)                2570
=================================================================
Total params: 329,962
Trainable params: 329,962
Non-trainable params: 0

　　让我们解读下，首先mnist为输入数据，尺寸大小为 (60000, 28, 28, 1)， 这是典型的NHWC结构，即（图片数量，宽度，高度，通道数）；

　　其次我们需要关注表格中的"output shape"输出尺寸，其遵循mnist一样的结构，只不过第一位往往是None，表示图片数待定，后三位则按照上述规则进行计算；

　　最后关注的是"param"可训练参数数量，不同的模型层计算方法不一样：

• 　　对于卷积层而言，假设过滤器尺寸为f * f， 过滤器数量为n， 若开启了bias，则bias数固定为1，输入图片的通道数为c，则param计算公式= (f * f * c + 1) * n；
• 　　对于池化层、flatten、dropout操作而言，是不需要训练参数的，所以param为0；
• 　　对于全连接层而言，假设输入的列向量大小为i，输出的列向量大小为o，若开启bias，则param计算公式为=i * o + o

　　按照代码中划分的三组模型层次，其输出尺寸和可训练参数数量的计算方法可如下图所示：

　　第一组：

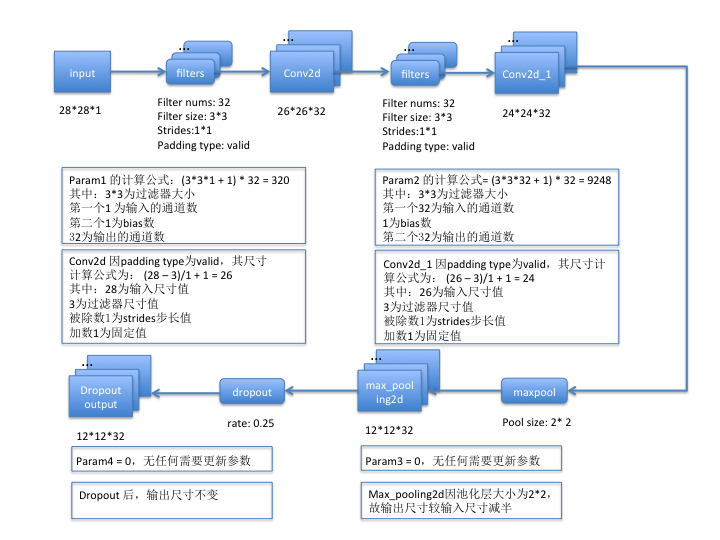
　　第二组：

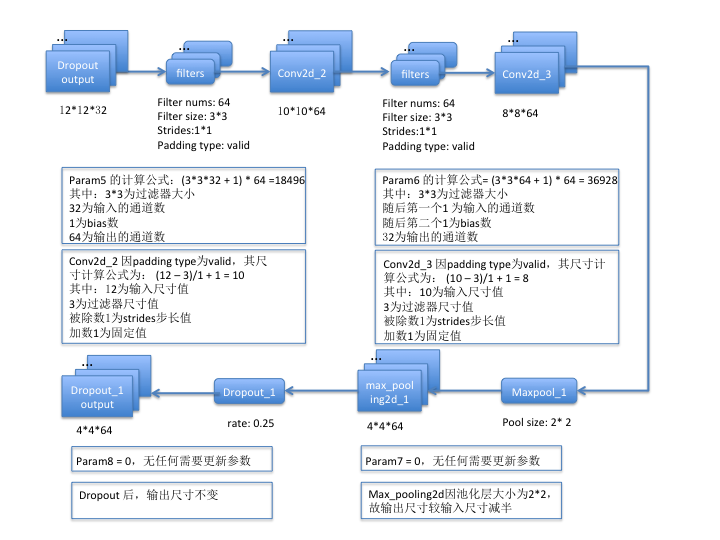
　　第三组：

　　

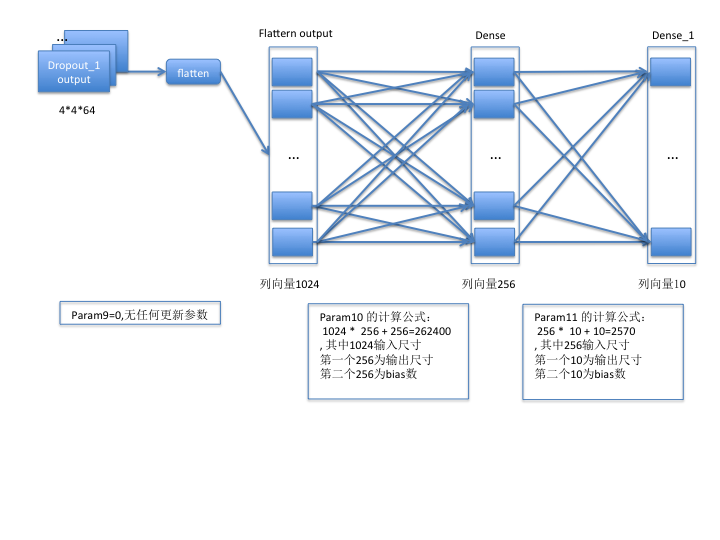
　　至此，模型各层的含义和相关计算方法已介绍完毕，希望此文能帮助大家更好地理解模型的构成和相关计算。