[PyTorch]PyTorch中反卷积的用法

文章来源：https://www.jianshu.com/p/01577e86e506

pytorch中的 2D 卷积层 和 2D 反卷积层 函数分别如下：

 class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, groups=1, bias=True)

class torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, bias=True)

我不禁有疑问：

• 问题1： 两个函数的参数为什么几乎一致呢？
• 问题2： 反卷积层中的 output_padding是什么意思呢？
• 问题3： 反卷积层如何计算input和output的形状关系呢？
  
  看了中文文档后，我得不出答案，看了英文文档，才弄明白了。花费了一个下午的时间去研究这个问题，值得用此文纪录一下。

我们知道，在卷积层中，输入输出的形状关系为：

o = [ (i + 2p - k)/s ] +1 （1）

其中：

• O : 为 output size
• i: 为 input size
• p: 为 padding size
• k: 为kernel size
• s: 为 stride size
• [] 为下取整运算

(1) 当 S=1 时

若 s等于1，则公式（1）中的取整符号消失，o 与 i 为 一一对应 的关系。 我们有结论：

如果卷积层函数和反卷积层函数的 kernel_size, padding size参数相同（且 stride= 1），设反卷基层的输入输出形状为 i' 和 o', 卷积层的输入输出形状i和o, 则它们为 交叉对应 的关系，即：

i = o'
o = i'

为回答问题3, 我们将上述关系代入公式中，即：

i' = o' + 2p - k +1

已知 i', 即可推出 o':

o' = i' - 2p + k - 1 （2）

摘两个例子：

(2) 当 S>1 时

若 S>1 , 则公式（1）中的取整符号不能消去，o 与 i 为 多对1 的关系。 效仿 S=1时的情形, 我们有结论：

如果卷积层函数和反卷积层函数的 kernel_size, padding size参数相同（且 stride>1），设反卷基层的输入输出形状为 i' 和 o', 卷积层的输入输出形状i和o,

i' = [ (o' + 2p - k)/s ] +1

已知 i', 我们可以得出 s 个 o' 解:

o'(0) = ( i' - 1) x s + k - 2p
o'(1) = o'(1) + 1
o'(2) = o'(1) + 2
...
o'(s-1) = o'(1) + s-1

即：

o'(n) =o'(1) + n = ( i' - 1) x s + k - 2p + n,
n = {0, 1, 2...s-1}

为了确定唯一的 o' 解， 我们用反卷积层函数中的ouput padding参数指定公式中的 n 值。这样，我们就回答了问题（2）。

摘一个简单的例子：

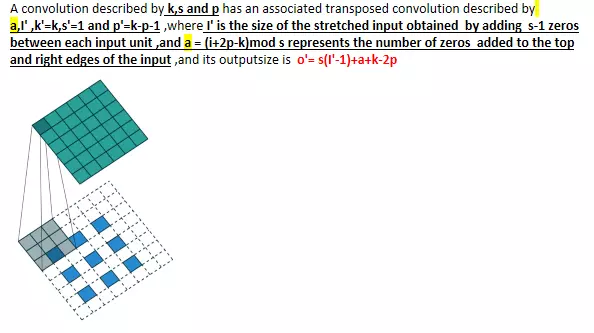
(3) 实验验证

给出一小段测试代码，改变各个参数值，运行比较来验证上面得出的结论，have fun~.

from torch import nn
from torch.nn import init
from torch.autograd import Variable

dconv = nn.ConvTranspose2d(in_channels=1, out_channels= 1,  kernel_size=2, stride=2, padding=1,output_padding=0, bias= False)
init.constant(dconv.weight, 1)
print(dconv.weight)

input = Variable(torch.ones(1, 1, 2, 2))
print(input)
print(dconv(input))