Opencv 图片直方图
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
Mat img1, img2, img3, img_gray, map_x, map_y;
char win1[] = "window1";
char win2[] = "window2";
char win3[] = "window3";
char win4[] = "window4";
int threshold_value = 0;
int max_value = 255;
RNG rng(12345);
int Demo_Histogram();
int index = 0;
//Remap
int Demo_Histogram()
{
img1 = imread("D://images//1//9.jpg");
if (img1.empty())
{
cout << "could not load image..." << endl;
return 0;
}
imshow(win1, img1);
vector<Mat> bgr_planes;
//把多通道图像分为多个单通道图像
split(img1,bgr_planes);
//imshow(win2,bgr_planes);
int histSize = 256;
float range[] = {0,256};
const float *histRanges = {range};
Mat b_hist, g_hist, r_hist;
calcHist(&bgr_planes[0], 1, 0, Mat(), b_hist, 1, &histSize, &histRanges, true, false);
calcHist(&bgr_planes[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRanges, true, false);
calcHist(&bgr_planes[2], 1, 0, Mat(), r_hist, 1, &histSize, &histRanges, true, false);
int hist_h = 400;
int hist_w = 512;
int bin_w = hist_w / histSize;
Mat histImage(hist_w,hist_h,CV_8UC3,Scalar(0,0,0));
//归一化处理
normalize(b_hist, b_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
normalize(g_hist, g_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
normalize(r_hist, r_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
for (int i=1;i<histSize;i++)
{
line(histImage,
Point((i-1)*bin_w,hist_h-cvRound(b_hist.at<float>(i-1))),
Point((i)*bin_w, hist_h - cvRound(b_hist.at<float>(i))),
Scalar(255,0,2),2,LINE_AA);
line(histImage,
Point((i - 1)*bin_w, hist_h - cvRound(g_hist.at<float>(i - 1))),
Point((i)*bin_w, hist_h - cvRound(g_hist.at<float>(i))),
Scalar(0, 255, 2), 2, LINE_AA);
line(histImage,
Point((i - 1)*bin_w, hist_h - cvRound(r_hist.at<float>(i - 1))),
Point((i)*bin_w, hist_h - cvRound(r_hist.at<float>(i))),
Scalar(0, 0, 255), 2, LINE_AA);
}
imshow(win2, histImage);
return 0;
}
int main()
{
Demo_Histogram();
waitKey(0);
return 0;
}
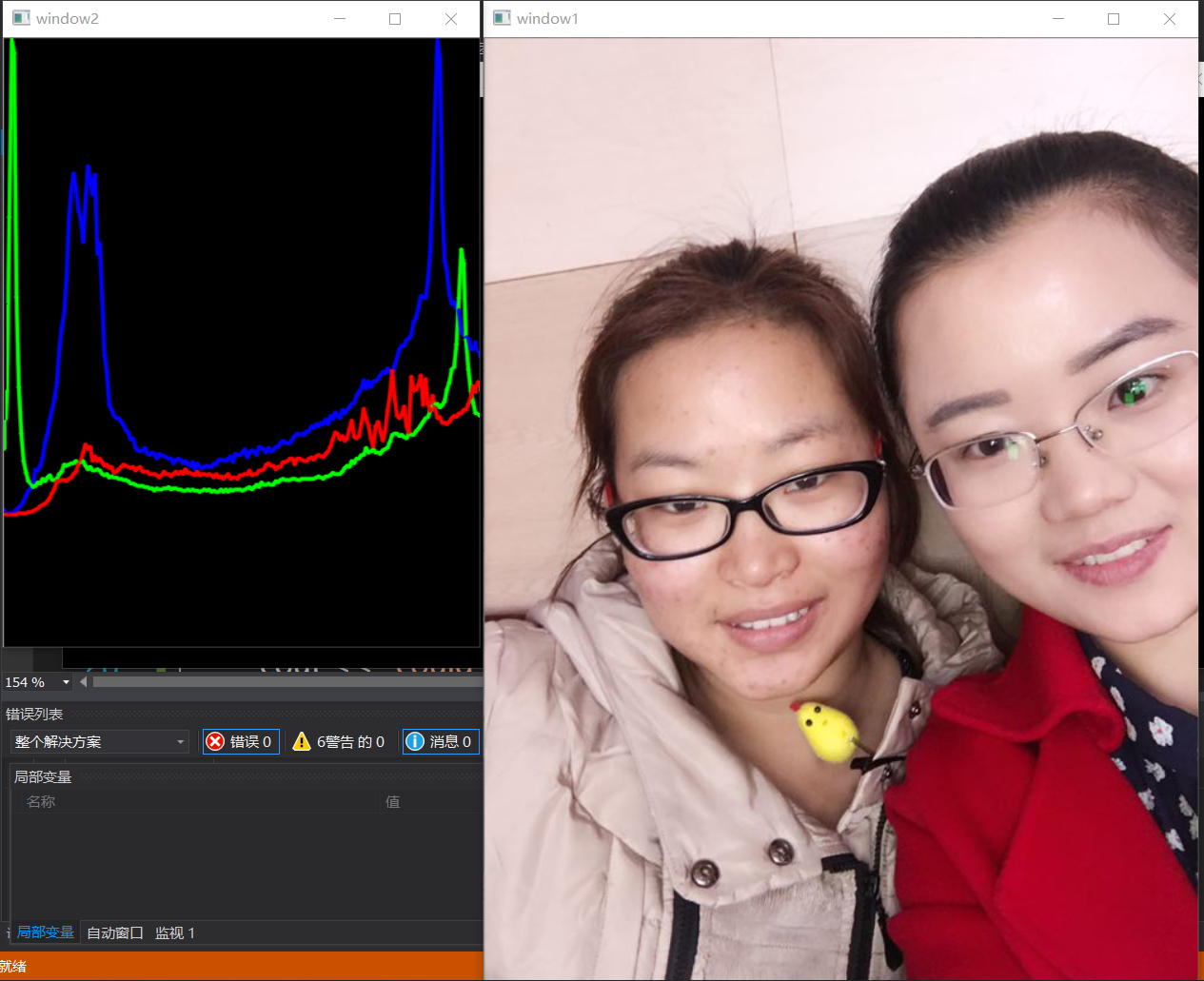
Opencv 图片直方图的更多相关文章
- 【计算机视觉】OpenCV中直方图处理函数简述
计算直方图calcHist 直方图是对数据集合的统计 ,并将统计结果分布于一系列提前定义的bins中.这里的数据不只指的是灰度值 ,统计数据可能是不论什么能有效描写叙述图像的特征. 如果有一个矩阵包括 ...
- opencv——图像直方图与反向投影
引言 在图像处理中,对于直方图这个概念,肯定不会陌生.但是其原理真的可以信手拈来吗? 本文篇幅有点长,在此列个目录,大家可以跳着看: 分析图像直方图的概念,以及opencv函数calcHist()对于 ...
- 基于opencv图片切割
基于opencv图片切割为n个3*3区块 工作原因,切割图片,任务急,暂留调通的源码,留以后用. package com.rosetta.image.test; import org.opencv.c ...
- Opencv图片明暗处理
Opencv图片明暗处理 #include <iostream> #include <opencv2/opencv.hpp> using namespace std; usin ...
- Python OpenCV图片转视频 工具贴(三)
Python OpenCV图片转视频 粘贴即用,注意使用时最好把自己的文件按照数字顺序命名.按照引导输入操作. # 一键傻瓜式引导图片串成视频 # 注意使用前最好把文件命名为数字顺序格式 import ...
- python opencv 图片缺陷检测(讲解直方图以及相关系数对比法)
一.利用直方图的方式进行批量的图片缺陷检测(方法简单) 二.步骤(完整代码见最后) 2.1灰度转换(将原图和要检测对比的图分开灰度化) 灰度化的作用是因为后面的直方图比较需要以像素256为基准进行相关 ...
- opencv图像直方图均衡化及其原理
直方图均衡化是什么有什么用 先说什么是直方图均衡化,通俗的说,以灰度图为例,原图的某一个像素为x,经过某个函数变为y.形成新的图.新的图的灰度值的分布是均匀的,这个过程就叫直方图均衡化. 图像直方图均 ...
- opencv —— equalizeHist 直方图均衡化实现对比度增强
直方图均匀化简介 从这张未经处理的灰度图可以看出,其灰度集中在非常小的一个范围内.这就导致了图片的强弱对比不强烈. 直方图均衡化的目的,就是把原始的直方图变换为在整个灰度范围(0~255)内均匀分布的 ...
- opencv 比较直方图方式 进行人脸检测对比
完整opencv(emgucv)人脸.检测.采集.识别.匹配.对比 //成对几何直方图匹配 public static string MatchHist() ...
随机推荐
- 笔记:加密 RSA AES
笔记:加密 RSA AES RSA 是非对称加密,有公钥和私钥. RSA算法原理(一) http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_par ...
- Mac下docker搭建lnmp环境 + redis + elasticsearch
之前在windows下一直使用vagrant做开发, 团队里面也是各种开发环境,几个人也没有统一环境,各种上线都是人肉,偶尔还会有因为开发.测试.生产环境由于软件版本或者配置不一致产生的问题, 今年准 ...
- php端安装rabbitmq-c
php端安装rabbitmq-c url:https://github.com/alanxz/rabbitmq-c cd rabbitmq-c**** ./configure --prefix=/us ...
- 【kubernetes】kubectl logs connection refused
因为启动dashboard报CrashLoopBackOff错误,尝试使用logs去查看日志,结果报错,错误如下: [root@localhost ~]# kubectl -s http://192. ...
- node中的ajax提交小例子
我们看一个HTML5页面中通过AJAX请求的方式获取HTTP服务器返回数据的代码示例.由于我们把服务器的端口指定为1337,并将从端口为80的网站中运行HTML5页面,因此这是一种跨域操作,需要在HT ...
- 数据结构和算法之:二分法demo
package com.js.ai.modules.pointwall.testxfz; class OrdArray{ private long[] a; private int nElems; p ...
- Ceph在OpenStack中的地位
对Ceph在OpenStack中的价值进行简要介绍,并且对Ceph和Swift进行对比. 对于一个IaaS系统,涉及到存储的部分主要是块存储服务模块.对象存储服务模块.镜像管理模块和计算服务模块.具体 ...
- 19_java之List和Set
01List接口的特点 A:List接口的特点: a:它是一个元素存取有序的集合. 例如,存元素的顺序是11.22.33.那么集合中,元素的存储就是按照11.22.33的顺序完成的). b:它是一 ...
- 11_java之接口和多态
01接口的概念 * A:接口的概念 接口是功能的集合,同样可看做是一种数据类型,是比抽象类更为抽象的”类”. 接口只描述所应该具备的方法,并没有具体实现,具体的实现由接口的实现类(相当于接口的子类)来 ...
- postman 中url有动态变换的值时,可以按下面方式变换。
get 和post均适用.
